Understanding time complexity:
Constant time operation: if an operation has nothing to do with the amount of data, it is completed within a fixed time every time, which is called constant operation.
Time complexity is an indicator of the number of constant operations in an algorithm flow. It is often represented by 0 (pronounced big0). Specifically, in the expression of constant operation quantity, as long as the high-order term, not the low-order term, and not the coefficient of the high-order term, if the remaining part is recorded as f (N), the time complexity is O (f (N)).
To evaluate the quality of an algorithm flow, first look at the index of time complexity, and then analyze the actual running time under different data samples, that is, the constant term time.

Answer: the time complexity of algorithm 1 is O(M*N),
The time complexity of algorithm 2 is O(M*logN),
The time complexity of algorithm 3 is O(M*logM)+O(N+M),
Bubble sorting: time complexity O(N^2)
Graphic process:
Assuming that the sequence to be sorted is (5,1,4,2,8), if bubble sorting is used to sort them in ascending order (from small to large), the whole sorting process is as follows:
1) In the first round of sorting, at this time, the elements in the whole sequence are located in the sequence to be sorted. Scan each pair of adjacent elements in turn, and exchange positions for element pairs with incorrect order. The whole process is shown in Figure 1.
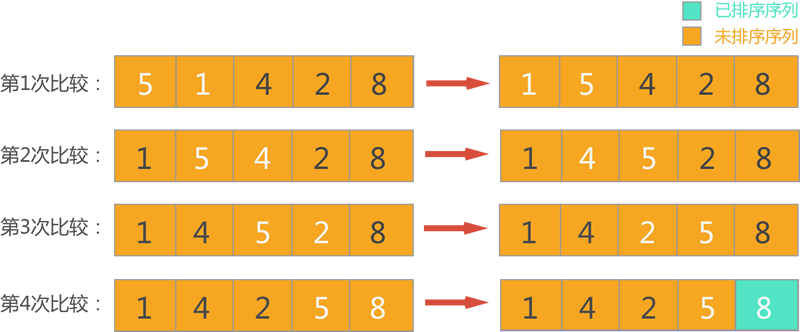
Figure 1 first round sorting (white font indicates a pair of adjacent elements participating in the comparison)
As can be seen from Figure 1, after the first round of bubble sorting, the maximum number of 8 is found from the sequence to be sorted, and it is placed at the end of the sequence to be sorted and incorporated into the sorted sequence.
2) In the second round of sorting, at this time, the sequence to be sorted only contains the first four elements. Scan each pair of adjacent elements in turn, and exchange positions for elements with incorrect order. The whole process is shown in Figure 2.
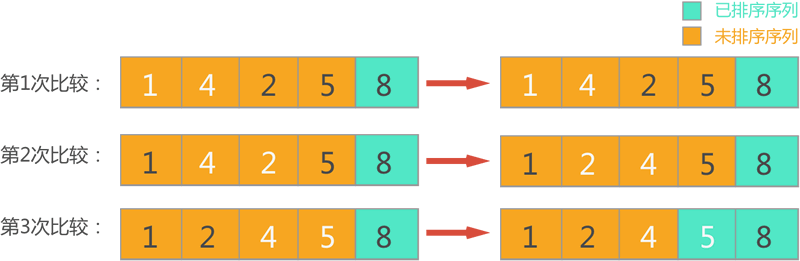
Figure 2 second round sorting (white font indicates a pair of adjacent elements participating in the comparison)
As can be seen from Figure 2 #, after the second round of bubble sorting, the maximum number of 5 is found from the sequence to be sorted, and it is placed at the tail of the sequence to be sorted and incorporated into the sorted sequence.
3) The third round of sorting. At this time, the sequence to be sorted contains the first three elements. Scan each pair of adjacent elements in turn, and exchange positions for elements with incorrect order. The whole process is shown in Figure 3.
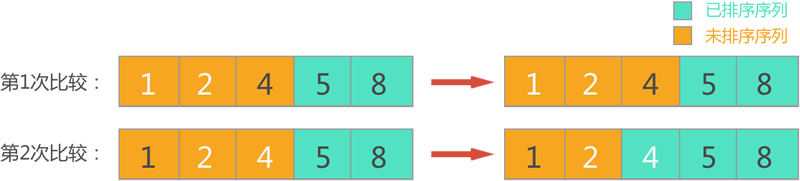
Figure 3 the third round of sorting (white font indicates a pair of adjacent elements participating in the comparison)
After this round of bubble sorting, the maximum number of 4 is found from the sequence to be sorted, and it is placed at the end of the sequence to be sorted and incorporated into the sorted sequence.
4) The fourth round of sorting. At this time, the sequence to be sorted contains the first two elements. The whole process of bubble sorting is shown in Figure 4.

Figure 4 the fourth round of sorting (white font indicates a pair of adjacent elements participating in the comparison)
After this round of bubble sorting, the maximum number 2 is found out from the sequence to be sorted, put it at the end of the sequence to be sorted and incorporated into the sorted sequence.
5) When the fifth round of bubble sorting is carried out, since there is only one element left in the sequence to be sorted, no matter the comparison of adjacent elements is carried out, it is directly incorporated into the sorted sequence, and the sequence at this time is recognized as the sorted sequence (as shown in Figure 5).

Figure 5 bubble sorted sequence
Code process:
package basic_package_01;
import java.util.Arrays;
// Bubbling algorithm
public class Code_01_BuddleSort {
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return; //The sorted element is not empty and must be greater than or equal to 2 elements.
}
int m = 1; //Sorting rounds count
for(int end = arr.length-1; end > 0; end--) {
for(int i = 0; i < end; i++) {
if(arr[i] > arr[i+1]) {
swap(arr, i, i+1);
}
}
System.out.print("The first"+ m +"Round bubble sorting");
m++;
printArray(arr); //Print sequence
}
}
private static void swap(int[] arr, int i, int j) {
// TODO Auto-generated method stub
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// Function of print sequence
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {5,1,4,2,8};
System.out.print("Sequence to be sorted:");
printArray(arr); //Print original array
bubbleSort(arr);
System.out.print("Final sequence:");
printArray(arr); //Print results
}
}
Code result (terminal output):

Note: some contents of this part are quoted as follows: Bubble sorting algorithm (super detailed)