Classification of 0 sort

1. Stability and Instability: Is the Relative Position of Equal Numbers Changing
2. Internal and External Sorting: Whether to Use External Storage

1 insertion sort

Ideas:

1. Starting with the first element, build an ordered ordering
2. Find the right place to insert one by one in the ordered order ahead

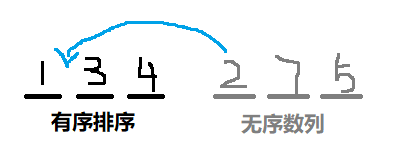
Time complexity:

• Best case: order T=O(n)T=O(n)T=O(n) T = O (n)
• Worst case: reverse order T=O(n2)T=O(n^2)T=O(n2)

Classification: stable, internal ranking

// Insertion sort
void insertion_sort(int data[], int len){
	// If length <= 1, exit without sorting
	if( len <= 1 ){
		return;
	}
	
	// Number of comparisons and exchanges
	int compareCount = 0;
	int swapCount = 0;
	
	// sort
	int i,j;
	// Insert the preceding ordered array from the second bit, with the subscript of 1
	for ( i=1; i<len; i++){
		int tmp = data[i]; // The first of an unordered array
		
		for ( j=i-1; j>=0; j-- ){
			compareCount++;
			if(data[j] <= tmp){
				break;
			}else{
				data[j+1] = data[j];
			}
		}
		swapCount++;
		data[j+1] = tmp;
	}
	printf("Number of insert sort comparisons:%d\n", compareCount);
	printf("Insert Sort Exchange Number:%d\n", swapCount);
}

2 Bubble Sorting

Ideas:

1. Starting from the first number each time, the adjacent elements are compared in turn, the order is unchanged, and the reverse order is exchanged.
2. The largest number must be in the last place. Next time, compare it with the first one.
3. break a process without exchange order
   
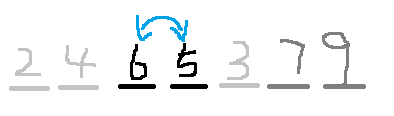
   Time complexity:

• Best case: order T=O(n)T=O(n)T=O(n) T = O (n)
• Worst case: reverse order T=O(n2)T=O(n^2)T=O(n2)

Classification: stable, internal ranking

// Exchange function, C language needs to pass in pointer to exchange
void swap(int *a, int *b){
	int tmp;
	tmp = *a;
	*a = *b;
	*b = tmp;
}

// Bubble sort
void Bubble_sort(int data[], int len){
	int k = 0;
	int compareCount = 0; // Record the number of comparisons
	int swapCount = 0; // Record Exchange Number
	
	while(1) {
		bool done = false; // Determine if there is at least a sequential exchange in the loop
		
		int i;
		for( i=0; i<len-1-k; i++ ){
			compareCount++; // Number of comparisons + 1
			if( data[i] < data[i+1]){
				continue;
			}
			
			swap(&data[i], &data[i+1]); // Need to change the incoming address
			swapCount++; // Exchange times + 1
			done = true;
		}
		if(!done){
			break;
		}
		
		k++;
	}
	printf("Bubble sort comparison times:%d\n", compareCount);
	printf("Bubble Sort Exchange Number:%d\n", swapCount);
}

3 Hill Sorting

Optimized version of insert sort
Ideas:

1. Define the decrement sequence D1>D2>...> D k>...> D n = 1D_1> D_2>...> D_k>...> D_n = 1D1 > D_2 > Dk > Dn = 1
2. Insert and sort subcolumns in the list with intervals of DkD_kDk in turn
   
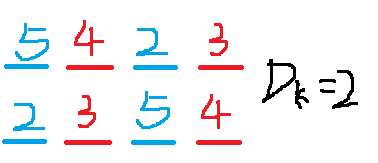
   Time complexity:
   Influenced by interval selection

Classification: Unstable, Internal Sorting

// The insertion sort of the subcolumn, which considers D as 1, is the normal insertion sort.
// Input: starting point, number of nodes, spacing
void Insert_sort(int data[], int len, int D){
	// Determine whether insertion sort is needed
	if ( len <= 1 ){
		return;
	}
	
	// Insert Sort: Ordered + Unordered
	// Each subcolumn
	int i;
	for(i=D; i<len*D; i+=D){
		int j, tmp = data[i];
		
		// Unordered insertion order (reverse comparison from ordered tail)
		for (j=i-D; j>=0; j-=D){
			if (data[j] <= tmp ){
				break;
			}
			
			data[j+D] = data[j];
		}
		data[j+D] = tmp;
	}
}

// Shell Sort
void Shell_sort(int data[], int len ){

	/* Determine whether insertion sort is needed */ 
	if ( len <= 1 ){
		return;
	}
	
	/* Partition subcolumn */ 
	int D; // interval
	for (D=len/2; D>0; D/=2){
		// Operations on different subcolumns in turn
		int k;
		for (k=0; k<D; k++){
			Insert_sort(data+k, len/D, D);
		}
	}
}

4 Selective Sorting

Ideas:

• Starting from the first place, always choose the smallest number to put in
  
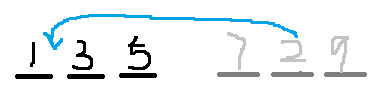
  Time complexity:
  T=O(n2)T=O(n^2)T=O(n2)

// exchange
void swap(int *a, int *b){
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

// Selective Sorting
void Selection_sort(int data[], int len){
	int compareCount = 0;
	int swapCount=0;
	
	int i;
	for( i=0; i<len; i++ ){
		int minIndex = i;
		int j;
		for ( j=i+1; j<len; j++ ){
			compareCount++;
			if( data[j] < data[minIndex] ){
				minIndex = j;
			}
		}
		// Insert the smallest into the corresponding position
		swapCount++;
		swap(&data[i], &data[minIndex]);
	}
	
	printf("The number of comparisons in the selection order:%d\n", compareCount);
	printf("Select the number of swaps for sorting:%d\n", swapCount);

5 Quick Sorting

Thought: Recursion

1. Find a fulcrum position

• Initialization: iii is at the top of the column to be sorted, and jjj is at the end of the column to be sorted
• Comparing the number of iii and j j j positions from right to left, order j_1j-1j_1, reverse order exchange
• Comparing the number of jjj and I I I positions from left to right, order i+1i+1i+1, reverse order exchange
• I & lt; Ji & lt; Ji < j, return to the position of the central axis

1. Line up the left side - go back to step 1
2. Line up the right side - go back to step 1

Time complexity: T=O(nlog(n))T=O(nlog(n))T=O(nlog(n)) T = O (nlog (n))
Classification: instability

// Commutative function
void swap(int *a, int *b){
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

/* partition */
int Partition(int data[], int len){
	// Determine whether the length needs to be executed
	if (len <= 1){
		return 0;
	}
	
	int i = 0; // Initial i is at the head of the column to be sorted
	int j = len-1; //Initial j is at the end of the column to be sorted
	while(i<j){
		// Comparing the number of positions i and j from right to left, order j-1, reverse order exchange
		while(data[i]<=data[j] && i<j){
			j--; // Sequence j-1
		}
		swap(&data[i], &data[j]); // Inverse Sequence Exchange
		
		// Comparing the number of positions i and j from left to right, order i+1, reverse order exchange
		while(data[i]<=data[j] && i<j){
			i++; // Sequence i+1
		}
		swap(&data[i], &data[j]); // Inverse Sequence Exchange
	}
	return i; // Return to the center axis = Left Length
}

// Recursive execution partition
void Quick_sort(int data[], int len){
	// Determine whether the length needs to be executed
	if (len <= 1){
		return;
	}
	
	// Recursive execution partition
	int pivot = Partition(data, len);// partition
	Quick_sort(data, pivot);
	Quick_sort(data+pivot+1, len-pivot-1);
}