Novice Xiaobai is here again. Write a blog to record his problem making process.
I find that blogging will make me more motivated to do questions. Now it's a holiday. I write about two or three questions every day. I hope I can stick to it after school starts. I don't say two or three questions every day. I wish I could stick to one question every day.
There are N (> 0) integers in AN array A. on the premise of not allowing the use of other arrays, move each integer cycle M (≥ 0) positions to the right, that is, transform the data in a from (A0 A1 * AN − 1) to (AN − M * AN − 1 A0 A1 * AN − M − 1) (the last M number cycles to the top M positions). If you need to consider the number of times the program moves data as little as possible, how to design the method of moving?
Input format:
Each input contains a test case, and the first line inputs N (1 ≤ N ≤ 100) and M (≥ 0); On line 2, enter N integers separated by spaces.
Output format:
In one line, the integer sequence after M bits of cyclic right shift is output, which is separated by spaces, and there can be no redundant spaces at the end of the sequence.
Input sample:
6 2 1 2 3 4 5 6
Output example:
5 6 1 2 3 4
The initial idea is to start with the number with subscript 0. Anyway, the array is placed in order. Move it to the position of coordinate + 1-M and then take the N remainder. The number in the original position is placed on the middle number count, and the next one moves the middle number. According to the above rules, move it n-1 times and stop. It can be output. If it is not placed in order, just record its coordinates. But maybe this is not the easiest way. The number in each position should be moved once.
Then I thought again. If it is orderly, I don't just record N and M, find the first number, add 1 to the following numbers in turn, and then take the remainder to output. I don't have to create an intermediate value, and then change the position. I can output it directly.
The code written is as follows:
#include<iostream>
using namespace std;
int main(){
int N,M;
cin>>N>>M;
for(int i=0;i<N;i++){
if(i>0)
cout<<" ";
cout<<(N-M+i+1)%N;
}
return 0;
}However, this writing ignores that when it is used as the original number, the value obtained by taking the remainder is 0
So I changed it
#include<iostream>
using namespace std;
int main(){
int N,M;
cin>>N>>M;
for(int i=0;i<N;i++){
if(i>0)
cout<<" ";
if(M-i-1==0)
cout<<N;
else
cout<<(N-M+i+1)%N;
}
return 0;
}But only one is right, so I guess it may not be orderly. I should follow my first idea. You need two intermediate values and a temp to record its coordinates.
However, I found that the idea of a temp can only correspond to the case where m is not a factor of N. if M is a factor of N, this will form a ring. For example, if I start from arr[0] and jump m grids each time, its subscript will range from 0 to 2, 2 to 4, 4 to 0 (because it is a subscript, there is no 6, only 5), so in this case, it needs M intermediate numbers, The intermediate values start from arr[0],arr[1] to arr[M-1]. From the example, we need two rings: 0 and 1.
The final code is as follows:
#include<iostream>
using namespace std;
int main(){
int N,M,temp,count1=0,count2=0,k=1;
cin>>N>>M;
int *arr=new int[N];
for(int i=0;i<N;i++){
cin>>arr[i];
}
int h=N;
if(M==0)
goto thisi;
if(N%M==0){
k=M;
h=N/M;
}
for(int j=0;j<k;j++){
count1=arr[M+j],temp=M+j,arr[temp]=arr[j];//first exchange
for(int i=1;i<h;i++){
temp=(temp+M)%N;
if(i%2==1){
count2=arr[temp];
arr[temp]=count1;
}
else{
count1=arr[temp];
arr[temp]=count2;
}
}
}
thisi:
for(int i=0;i<N;i++){
if(i>0)
cout<<" ";
cout<<arr[i];
}
return 0;
}The case of M=0 is added once after submission, but even if it is changed to this way, it is only right for three. I don't quite understand why.
This is the code I implemented on other compilers:
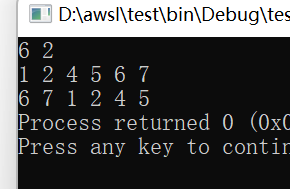I feel no problem.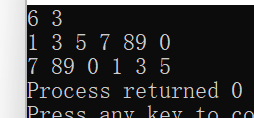
However, the results are not very satisfactory.
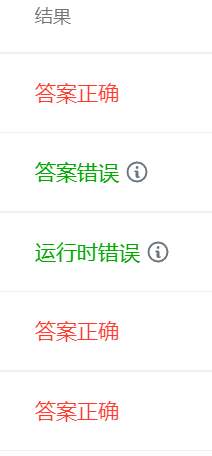
Confused, I don't know what's wrong with my thinking. Look at someone else's code.
After reading other people's, I suddenly find that I think too much and complex. My first idea is completely feasible. No matter whether the numbers given are regular or not, just remember the subscript, store them from the subscript M, and then output them in sequence. Unexpectedly simple, look sideways, smile and sigh silently. I think they are wonderful.
And there's another point, I didn't mention m < n (this is my wrong point. After adding this point, let m=m%n, the answers are all correct)
#include<iostream>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
int a[n];
m %= n;
for (int i = m; i < n; i++) {
cin >> a[i];
}
for (int i = 0; i < m; i++) {
cin >> a[i];
}
for (int i = 0; i < n; i++) {
cout << a[i];
if (i != n - 1)
cout << " ";
}
return 0;
}https://blog.csdn.net/qq_36122764/article/details/82056428
Then I looked at other people's code and got the way to solve it directly with library functions
The idea of this is to take out the last bit of the array, remember, move the others one grid back in turn, put the last bit just now to the first, and then repeat this action M times.
There is also a reversal idea, after reversing all numbers, reverse the former m, and then reverse the latter
Of course, the most important thing is to understand the reverse function, header algorithm, reverse first to last, reversible array and string. However, if you want to take the address &, which is used to flip the contents between [a,b), note that the front is a closed interval and the back is an open interval.
Inverts the string of the string class
string str="C++REVERSE"; reverse(str.begin(),str.end());//The str result is esrevert + + C
I found that the exchange code I thought about before is too complex. I want to record a number n1, find the position n2 where n1 will move forward, and then move the number on n2 forward M, find its moving position, and then move M forward. This is really too complicated. I have thought about the code for a long time.
Well, that's the end of the problem!