preface

Through the introduction in the previous section, we can calculate the camera motion, but we don't know the specific position of feature points in space. In monocular SLAM, we cannot obtain the depth information of pixels only by relying on a single image. We need to estimate the depth of map points by triangulation.

Triangulation

Triangulation refers to the observation of the same road mark through different positions, and the distance of the road mark is inferred from the observed position. As shown in the figure:

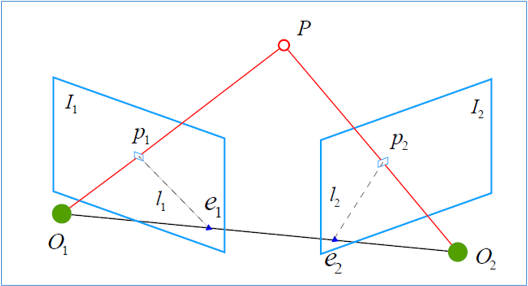
Ideally, O 1 P 1 O_{1} P_{1} O1 ＾ P1 ＾ and O 2 P 2 O_{2} P_{2} O2 ＾ P2 ＾ they intersect at P P P. However, due to the existence of noise, the two lines often cannot intersect. We can solve it by the least square method. According to the definition in epipolar geometry, we set x 1 x_{1} x1​， x 2 x_{2} x2 is the normalized coordinates of two feature points, then:

s 2 x 2 = s 1 R x 1 + t . s_{2} {x}_{2}=s_{1} {R} {x}_{1}+{t}. s2​x2​=s1​Rx1​+t.

Now we know R R R， t t t， x 1 x_{1} x1​， x 2 x_{2} x2, we want to solve it s 1 s_{1} s1​， s 2 s_{2} s2​. We can do this, for example, we want to solve s 1 s_{1} s1, you can multiply both sides left x 2 ∧ x_{2}^{\wedge} x2 Λ,, then:

s 2 x 2 ∧ x 2 = 0 = s 1 x 2 ∧ R x 1 + x 2 ∧ t s_{2} {x}_{2}^{\wedge} {x}_{2}=0=s_{1} {x}_{2}^{\wedge} {R} {x}_{1}+{x}_{2}^{\wedge} {t} s2​x2∧​x2​=0=s1​x2∧​Rx1​+x2∧​t

So only s 1 s_{1} s1 is an unknown number. We can easily solve it. Similarly s 2 s_{2} So is s2.

Practical triangulation

Basically, like the last code, the extra function is to calculate the depth information of feature points. The code is as follows:

#include <iostream>
#include <opencv2/opencv.hpp>
// #include "extra.h" // used in opencv2
using namespace std;
using namespace cv;

void find_feature_matches(
  const Mat &img_1, const Mat &img_2,
  std::vector<KeyPoint> &keypoints_1,
  std::vector<KeyPoint> &keypoints_2,
  std::vector<DMatch> &matches);

void pose_estimation_2d2d(
  const std::vector<KeyPoint> &keypoints_1,
  const std::vector<KeyPoint> &keypoints_2,
  const std::vector<DMatch> &matches,
  Mat &R, Mat &t);

void triangulation(
  const vector<KeyPoint> &keypoint_1,
  const vector<KeyPoint> &keypoint_2,
  const std::vector<DMatch> &matches,
  const Mat &R, const Mat &t,
  vector<Point3d> &points
);

///For drawing
inline cv::Scalar get_color(float depth) {
  float up_th = 50, low_th = 10, th_range = up_th - low_th;
  if (depth > up_th) depth = up_th;
  if (depth < low_th) depth = low_th;
  return cv::Scalar(255 * depth / th_range, 0, 255 * (1 - depth / th_range));
}

// Pixel coordinates to camera normalized coordinates
Point2f pixel2cam(const Point2d &p, const Mat &K);

int main(int argc, char **argv) {
  if (argc != 3) {
    cout << "usage: triangulation img1 img2" << endl;
    return 1;
  }
  //--Read image
  Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);

  vector<KeyPoint> keypoints_1, keypoints_2;
  vector<DMatch> matches;
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  cout << "Totally" << matches.size() << "Group matching point" << endl;

  //--Estimating motion between two images
  Mat R, t;
  pose_estimation_2d2d(keypoints_1, keypoints_2, matches, R, t);

  //--Triangulation
  vector<Point3d> points;
  triangulation(keypoints_1, keypoints_2, matches, R, t, points);

  //--Verify the re projection relationship between triangulated points and feature points
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  Mat img1_plot = img_1.clone();
  Mat img2_plot = img_2.clone();
  for (int i = 0; i < matches.size(); i++) {
    // First figure
    float depth1 = points[i].z;
    cout << "depth: " << depth1 << endl;
    Point2d pt1_cam = pixel2cam(keypoints_1[matches[i].queryIdx].pt, K);
    cv::circle(img1_plot, keypoints_1[matches[i].queryIdx].pt, 2, get_color(depth1), 2);

    // Second figure
    Mat pt2_trans = R * (Mat_<double>(3, 1) << points[i].x, points[i].y, points[i].z) + t;
    float depth2 = pt2_trans.at<double>(2, 0);
    cv::circle(img2_plot, keypoints_2[matches[i].trainIdx].pt, 2, get_color(depth2), 2);
  }
  cv::imshow("img 1", img1_plot);
  cv::imshow("img 2", img2_plot);
  cv::waitKey();

  return 0;
}

void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
  //--Initialization
  Mat descriptors_1, descriptors_2;
  // used in OpenCV3
  Ptr<FeatureDetector> detector = ORB::create();
  Ptr<DescriptorExtractor> descriptor = ORB::create();
  // use this if you are in OpenCV2
  // Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
  // Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
  Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //--Step 1: detect the corner position of Oriented FAST
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);

  //--Step 2: calculate the BRIEF descriptor according to the corner position
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);

  //--Step 3: match the BRIEF descriptors in the two images, using Hamming distance
  vector<DMatch> match;
  // BFMatcher matcher ( NORM_HAMMING );
  matcher->match(descriptors_1, descriptors_2, match);

  //--Step 4: match point pair filtering
  double min_dist = 10000, max_dist = 0;

  //Find out the minimum distance and maximum distance between all matches, that is, the distance between the most similar and the least similar two groups of points
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }

  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);

  //When the distance between descriptors is greater than twice the minimum distance, it is considered that the matching is wrong But sometimes the minimum distance is very small. Set an empirical value of 30 as the lower limit
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (match[i].distance <= max(2 * min_dist, 30.0)) {
      matches.push_back(match[i]);
    }
  }
}

void pose_estimation_2d2d(
  const std::vector<KeyPoint> &keypoints_1,
  const std::vector<KeyPoint> &keypoints_2,
  const std::vector<DMatch> &matches,
  Mat &R, Mat &t) {
  // Camera internal parameters, TUM Freiburg2
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);

  //--Convert matching points to vector < point2f >
  vector<Point2f> points1;
  vector<Point2f> points2;

  for (int i = 0; i < (int) matches.size(); i++) {
    points1.push_back(keypoints_1[matches[i].queryIdx].pt);
    points2.push_back(keypoints_2[matches[i].trainIdx].pt);
  }

  //--Compute essential matrix
  Point2d principal_point(325.1, 249.7);        //Camera master point, TUM dataset, calibration value
  int focal_length = 521;            //Camera focal length, TUM dataset, calibration value
  Mat essential_matrix;
  essential_matrix = findEssentialMat(points1, points2, focal_length, principal_point);

  //--Recover rotation and translation information from essential matrix
  recoverPose(essential_matrix, points1, points2, R, t, focal_length, principal_point);
}

void triangulation(
  const vector<KeyPoint> &keypoint_1,
  const vector<KeyPoint> &keypoint_2,
  const std::vector<DMatch> &matches,
  const Mat &R, const Mat &t,
  vector<Point3d> &points) {
  Mat T1 = (Mat_<float>(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
  Mat T2 = (Mat_<float>(3, 4) <<
    R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2), t.at<double>(0, 0),
    R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2), t.at<double>(1, 0),
    R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2), t.at<double>(2, 0)
  );

  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector<Point2f> pts_1, pts_2;
  for (DMatch m:matches) {
    // Convert pixel coordinates to camera coordinates
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }

  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);

  // Convert to non-homogeneous coordinates
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at<float>(3, 0); // normalization
    Point3d p(
      x.at<float>(0, 0),
      x.at<float>(1, 0),
      x.at<float>(2, 0)
    );
    points.push_back(p);
  }
}

Point2f pixel2cam(const Point2d &p, const Mat &K) {
  return Point2f
    (
      (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
      (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

discuss

Triangulation must have translation. In the case of pure rotation, triangulation cannot be carried out, that is to say, only translation can form a triangle. In the previous section, we also explained that if there is no translation, the epipolar constraint is always zero. If we emphasize the need for translation, it will lead to a contradictory problem. As shown in the figure:

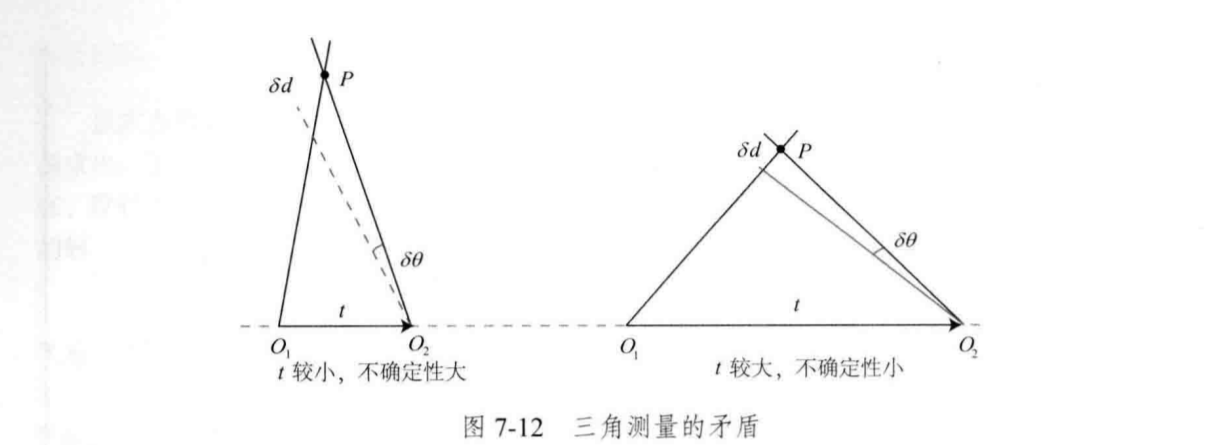
According to the geometric relationship in the figure above, when the translation is small, the uncertainty on the pixel will lead to large depth uncertainty; When the translation is larger, the influence of the error on the depth calculation is smaller. However, when the translation becomes larger, the appearance imaging of the image will change significantly. The greater the change, the more difficult it is to extract and match features. Therefore, there are contradictions: too much translation will lead to matching failure, too small translation and insufficient triangulation accuracy.