3.12 binary tree and heap

Binary tree

Definition of tree: a tree is a finite set of n (n > = 0) nodes. When n=0, it is called an empty tree.

In any non empty tree:
(1) There is only one specific node called root;
(2) When n > 1, the other nodes can be divided into m (M > 0) disjoint finite sets T1, T2 Tn，
Each set itself is a tree and is called the subtree of the root.

In addition, the definition of tree also needs to emphasize the following two points:
(1) When n > 0, the root node is unique, there can be no multiple root nodes, and the tree in the data structure can only have one root node.
(2) When m > 0, there is no limit on the number of subtrees, but they must be disjoint.
For any tree containing N nodes, there are and only n-1 edges.

A binary tree is a tree structure in which each node has at most two subtrees.
Subtrees are usually called "left subtree" and "right subtree".
Binary tree is often used to implement binary lookup tree and binary heap.

Binary tree is defined recursively, and its nodes are divided into left and right subtrees. Logically, binary tree has five basic forms:
(1) Empty binary tree
(2) Binary tree with only one root node
(3) Only left subtree
(4) Only right subtree
(5) Complete binary tree

Type of binary tree
(1) Full binary tree - a binary tree in which each node has left and right cotyledons except leaf nodes, and the leaf nodes are at the bottom.

From the perspective of graphic form, the full binary tree is a triangle in appearance.
Mathematically, the number of nodes in each layer of a full binary tree forms an equal ratio sequence with a first term of 1 and a common ratio of 2.
Therefore, the full binary tree satisfies the following properties from the formula of the equal ratio sequence.

1. The total number of points of a full binary tree with K layers is: \ (2^k − 1 \). Therefore, the number of nodes in a full binary tree must be odd.
2. The number of nodes on layer i is: \ (2^i − 1 \)
3. The number of leaf nodes (i.e. the last layer) of a full binary tree with K layers: \ (2^k − 1 \)

(2) Complete binary tree - if the height of the binary tree is h, the number of nodes in other layers (1 ~ h-1) reaches the maximum except layer H,
Layer h has leaf nodes, and leaf nodes are arranged from left to right, which is a complete binary tree.

1. All leaf nodes appear in layer K or k-1 (the two largest layers)
2. For any node, if the maximum level of its right subtree is l, the maximum level of its left subtree is l or L+1.

Some nouns of tree
Node hierarchy: defined from the root, the root is the first layer, and the child node of the root is the second layer, and so on;
Node degree: the number of subtrees contained in a node is called the degree of the node;
Height or depth of tree: the maximum level of nodes in the tree;
Tree degree: the degree of the largest node in a tree is called the degree of the tree;
Leaf node or terminal node: a node with a degree of 0 is called a leaf node;
Non terminal node or branch node: a node whose degree is not 0;
Ancestor of a node: all nodes from the root to the branch through which the node passes;
Parent node or parent node: if a node contains child nodes, this node is called the parent node of its child nodes;
Child node or child node: the root node of the subtree contained in a node is called the child node of the node;
Sibling node: nodes with the same parent node are called sibling nodes;
Cousin node: nodes with parents on the same layer are cousins to each other;
Descendant: any node in the subtree with a node as the root is called the descendant of the node.
Forest: a collection of m (m > = 0) disjoint trees is called forest;

The traversal of binary tree can be divided into the following types:

1. Preorder traversal: the traversal order rule is [left and right roots]
2. Middle order traversal: the traversal order rule is left root right
3. Post order traversal: the traversal order rule is left and right roots
4. Sequence traversal: the traversal sequence rule is [up, down, left and right]

[root left and right] is to traverse the root first, then the left subtree, and finally the right subtree; the so-called middle first and then the order of root nodes.
[sequence traversal is implemented through queue BFS]
After the left and right child nodes of the current node are queued, they are queued in turn, and the left and right child nodes of the queued node continue to queue until the traversal is completed.

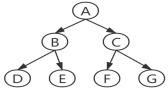
As shown in the above figure, the answers are as follows:
Preorder traversal: ABDECFG
Middle order traversal: DBEAFCG
Post order traversal: DEBFGCA
Sequence traversal: ABCDEFG

//Define the nodes of the tree
typedef struct Node{
    char data;
    struct Node *lch, *rch;
}Node, *Tree;

//Preorder traversal 
void preorderTraversal(Tree node){
    if(node!=NULL){
        cout<<node->data;
        preorderTraversal(node->lch);
        preorderTraversal(node->rch);
    }
}

//Medium order traversal
void inorderTraversal(Tree node){
    if(node!=NULL){
        inorderTraversal(node->lch);
        cout<<node->data;
        inorderTraversal(node->rch);
    }
}

//Postorder traversal
void postorderTraversal(Tree node){
    if(node!=NULL){
        postorderTraversal(node->lch);
        postorderTraversal(node->rch);
        cout<<node->data;
    }
}

1336: [example 3-1] find tree roots and children

[Title Description]
Given a tree, the root of the output tree, the node max with the most children and his children.

[input]
The first line: n (number of nodes ≤ 100), m (number of sides ≤ 200).
The following m lines: each line has two nodes X and y, indicating that y is the child of X (x,y ≤ 1000).

[output]
The first line: tree root;
The second line: node max with the most children;
The third line: max's children (output by number from small to small).

[input example]

8 7
4 1
4 2
1 3
1 5
2 6
2 7
2 8

[output example]

4
2 
6 7 8

[reference procedure]

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m,x,y, root=0, max_v=0, max_root=0;
int father[N];// father[i] represents the parent node of I

int main(){
    cin>>n>>m;
    for(int i=1; i<=m; i++){
        cin>>x>>y; father[y]=x;//x is the parent of y
    }
    for(int i=1; i<=n; i++){
        if(father[i]==0){//If there is no parent, it is the root node
            root=i; break;
        }
    }
    for(int i=1; i<=n; i++){
        int sum=0;
        for(int j=1; j<=n; j++){
            if(father[j]==i) {
                sum++;
            }
        }
        if(sum>max_v){//Node with the most children
            max_v=sum, max_root=i;
        }
    }
    cout<<root<<endl<<max_root<<endl;
    for(int i=1; i<=n; i++){
        if(father[i]==max_root){//max_ Child node of root
            cout<<i<<" ";
        }
    }
    return 0;
}

Traverse the tree according to the priority

[Title Description]
Enter a string of pre order traversal strings, and establish a binary tree according to this string.
For example, the following pre order traversal string: ABC##DE#G##F###
Where '#' represents a space, and the space character represents an empty tree.
After the binary tree is established, the binary tree is traversed in middle order and the traversal result is output.

[input format]
The input includes 1 line of string, and the length does not exceed 100.

[output format]
There may be multiple sets of test data. For each set of data,
Output the sequence traversed by the input string after establishing a binary tree, with a space after each character.
Each output result occupies one line.

[sample input] abc##de#g##f###
[sample output] c b e g d f a

[reference procedure]

#include<bits/stdc++.h>
using namespace std;
const int N=110;
char a[N];
int cnt=0;

typedef struct Node{
    char data;
    struct Node *lch, *rch;
}Node, *Tree;

//Recursive tree building
struct Node* build(){
    struct Node *root=NULL;
    if(a[cnt++]!='#'){
        root = (struct Node*)malloc(sizeof(struct Node));
        root->data = a[cnt-1];
        root->lch = build();
        root->rch = build();
    }
    return root;
}

//Medium order traversal
void inorder(struct Node *root){
    if(root!=NULL){
        inorder(root->lch);
        printf("%c ", root->data);
        inorder(root->rch);
    }
}

//Destroy binary tree
void del(struct Node* &root){
    if(root!=NULL){
        del(root->lch);
        del(root->rch);
        delete root;
        root = NULL;
    }
}
int main(){
    while(scanf("%s", a)!=EOF){
        cnt=0;
        struct Node *root=build();
        inorder(root);
        del(root);
        printf("\n");
    }
    return 0;
}

Build trees according to sequence traversal and medium sequence traversal

[Title Description]
Give the sequence traversal sequence and middle sequence traversal sequence of a binary tree,
Find the preorder traversal sequence and postorder traversal sequence of this binary tree.

[input format]
The first line is a positive integer N (1 < = N < = 30), representing the number of nodes of the binary tree (node numbers are 1~N).
The next two lines, each with N positive integers, represent the sequence traversal sequence and middle sequence traversal sequence of the binary tree respectively.
The data guarantees that each number of 1~N in the sequence appears only once.

[output format]
Output a line containing N positive integers, representing the preorder traversal sequence of the binary tree.
No additional spaces are output at the end of each line.

[sample input]

7
3 5 4 2 6 7 1
2 5 3 6 4 7 1

[sample output]

3 5 2 4 6 7 1

[reference procedure]

Build a tree according to preorder traversal and inorder traversal

[Title Description]
Given the preorder traversal and inorder traversal of a binary tree, find the postorder traversal of the binary tree.

[input format]
There are multiple groups of input data. The first line is an integer t (T < 1000), representing t groups of test data.
Each group includes two strings less than 50 in length,
The first string represents the preorder traversal sequence of the binary tree,
The second string represents the middle order traversal order of the binary tree.

[output format]
The first row of each group outputs the post order traversal sequence of the binary tree, and the second row outputs the hierarchical traversal sequence of the binary tree

[sample input]

2
abdegcf
dbgeafc
xnliu
lnixu

[sample output]

dgebfca
abcdefg
linux
xnuli

[reference procedure]

heap

Definition of heap: heap is a general term for a special kind of data structure in computer science.
Heap is usually an array object that can be regarded as a tree. It always satisfies the following properties:

1. The value of a node in the heap is always not greater than or less than the value of its parent node;
2. Heap is always a complete binary tree.

The heap with the largest root node is called the maximum heap or large root heap,
The heap with the smallest root node is called the smallest heap or small root heap.
Note: the elements in the heap are not necessarily sorted by array subscript order!!

Specific operations: (let's take the small root heap as an example)

1. Float up shift_up
   Starting from the current node, compare it with its parent node. If it is smaller than the parent node, exchange it,
   Then update the current queried node subscript to the original parent node subscript; Otherwise exit.

2. Sinking shift_down
   Compare the left and right sons (if any) of the current node, and exchange with it which is smaller,
   And update the subscript of the query node to the subscript of the exchanged child node, otherwise exit.

3. Insert push
   Every time we insert, we insert the last one and let it float up.

4. Pop up pop
   Pop up the top element of the heap, exchange the root node element with the tail node, and then let the current root element sink.

Heap insertion and deletion, each time O(logN)