150. Evaluation of inverse Polish expression

Title Link: 150. Inverse Polish expression evaluation (medium)

Title Description

Find the value of the expression according to the inverse Polish representation.

Valid operators include +, -, *, /. Each operand can be an integer or another inverse expression.

explain:

• Integer division preserves only the integer part.

• The given inverse Polish expression is always valid. In other words, an expression always yields a valid value and there is no case where the divisor is 0.

Example 1:

Input: tokens = ["2","1","+","3", "*"]
Output: 9
Explanation: this expression is transformed into a common infix arithmetic expression: ((2 + 1) * 3) = 9

Example 2:

Input: tokens = ["4","13","5", "/", "+"]
Output: 6
Explanation: this expression is transformed into a common infix arithmetic expression: (4 + (13 / 5)) = 6

Example 3:

Input: tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5", "+"]
Output: 22
Explanation:
This expression is transformed into a common infix arithmetic expression as follows:
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

Tips:

• 1 <= tokens.length <= 104

• tokens[i] is either an operator ("+", "-", "*" or "/") or an integer in the range [- 200, 200]

Inverse Polish expression:

Inverse Polish expression is a suffix expression. The so-called suffix means that the operator is written after it.

• The commonly used formula is an infix expression, such as (1 + 2) * (3 + 4).

• The inverse Polish expression of the formula is written as ((1,2 +) (3,4 +) *).

The inverse Polish expression has the following two advantages:

• After removing the brackets, the expression is unambiguous. Even if the above formula is written as 1 2 + 3 4 + *, the correct result can be calculated according to the order.

• Suitable for stack operation: enter the stack when encountering numbers; In case of an operator, take out the two numbers at the top of the stack for calculation, and press the result into the stack.

Problem solution

Idea: this problem is implemented by "stack", as shown in the figure below. When encountering numbers, it will be put into the stack, and when encountering characters, it will remove the two numbers at the top of the stack for calculation, and then push the result into the stack. In addition, the problem says that the given inverse Polish expression is always valid, so there is no need to judge whether the expression is valid or not.

 

 

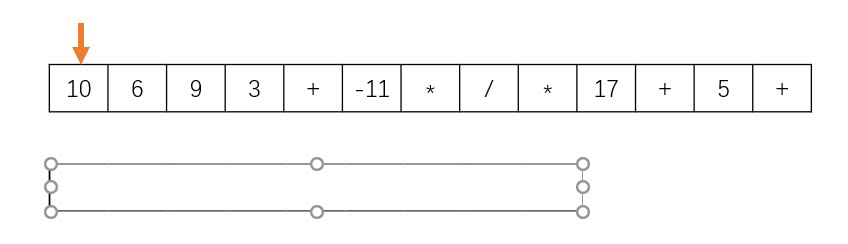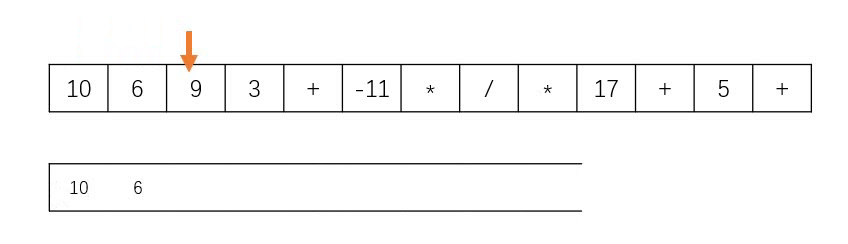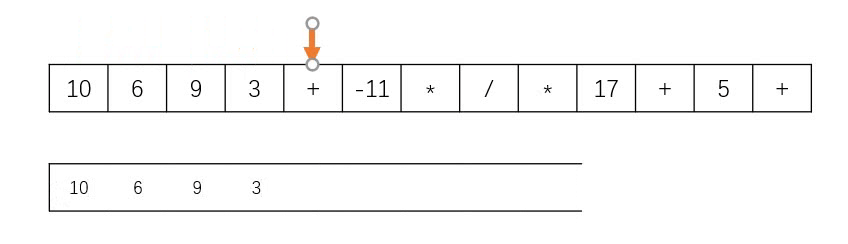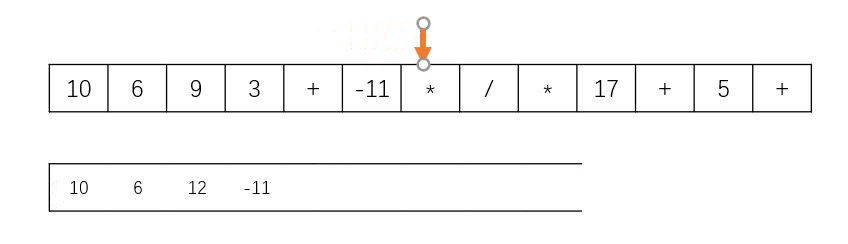
Code (C + +)

int evalRPN(vector<string>& tokens) {
    stack<string> sta;
    for (string t : tokens) {
        if (t == "+") {
            string temp1 = sta.top();
            sta.pop();
            string temp2 = sta.top();
            sta.pop();
            //stoi() take n Convert hexadecimal string to decimal
            int result = stoi(temp2) + stoi(temp1);
            sta.push(to_string(result));
        }
        else if (t == "-") {
            string temp1 = sta.top();
            sta.pop();
            string temp2 = sta.top();
            sta.pop();
            int result = stoi(temp2) - stoi(temp1);
            sta.push(to_string(result));
        }
        else if (t == "*") {
            string temp1 = sta.top();
            sta.pop();
            string temp2 = sta.top();
            sta.pop();
            int result = stoi(temp2) * stoi(temp1);
            sta.push(to_string(result));
        }
        else if (t == "/") {
            string temp1 = sta.top();
            sta.pop();
            string temp2 = sta.top();
            sta.pop();
            int result = stoi(temp2) / stoi(temp1);
            sta.push(to_string(result));
        }
        else {
            sta.push(t);
        }
    }
    return stoi(sta.top());
}

analysis:

• Time complexity: O(N), where N is the length of the vector.

• Space complexity: O(N).

Simplified code

int evalRPN(vector<string>& tokens) {
    stack<int> sta;
    for (string t : tokens) {
        if (t == "+" || t == "-" || t == "*" ||t == "/") {
            int temp1 = sta.top();
            sta.pop();
            int temp2 = sta.top();
            sta.pop();
            int result;
            if (t == "+") result = temp2 + temp1;
            else if (t == "-") result = temp2 - temp1;
            else if (t == "*") result = temp2 * temp1;
            else if (t == "/") result = temp2 / temp1;
            sta.push(result);
        } else {
            sta.push(stoi(t));
        }
    }
    return sta.top();
}