55. Minimum stack force buckle (LeetCode)

👉155. Minimum stack force buckle (LeetCode)

Topic Description: design push, pop, top and getMin functions, and find the minimum value when the time complexity is O(1)
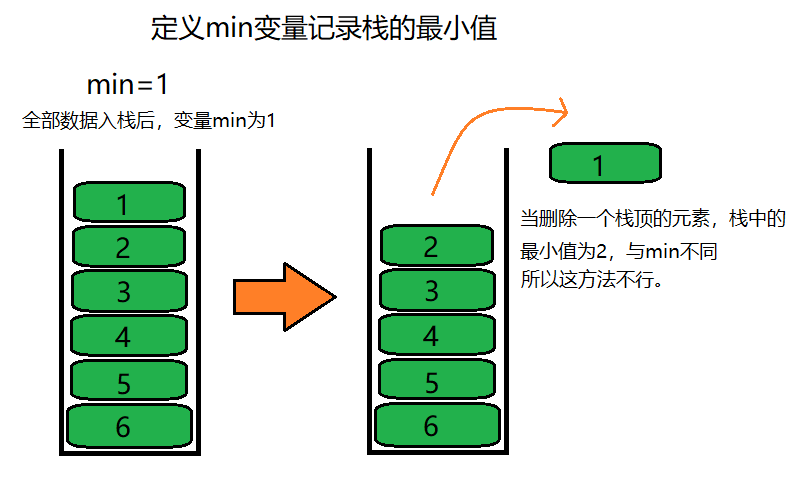
Wrong idea: given a variable to record the minimum value, this idea is wrong, and we should consider the problem more comprehensively.
When we stack {6, 5, 4, 3, 2, 1}, the variable that records the minimum value each time changes with each stack. When all the data is stacked, the variable that records the minimum value is 1. If the data is not deleted, The minimum value can be found with the time complexity of O (1), but if an element at the top of the stack is deleted, the minimum value in the stack also changes and does not match the variable recording the minimum value.

Correct problem solution

Through the above wrong ideas, we can improve them.
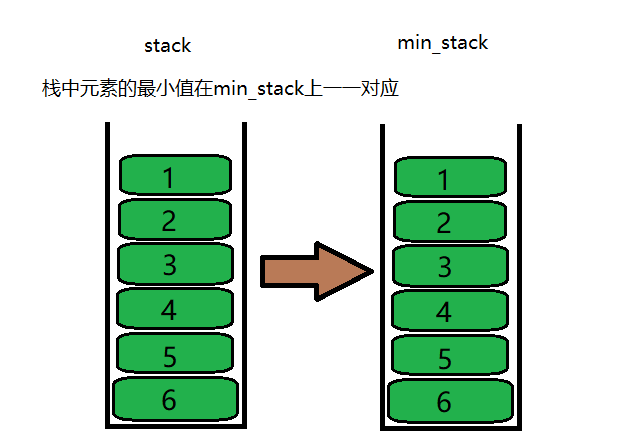
Every time an element is put into the stack, the minimum value in the current stack is recorded and stored in another stack.
For example: {6, 5, 4, 3, 2, 1}
When 6 is put into the stack, the minimum value of elements in the current stack is 6;
When 5 enters the stack, the minimum value of elements in the current stack is 5;
When 4 enters the stack, the minimum value of elements in the current stack is 4;
When 3 enters the stack, the minimum value of elements in the current stack is 3;
When 2 enters the stack, the minimum value of elements in the current stack is 2;
When 1 enters the stack, the minimum value of elements in the current stack is 1;
Store the smallest element of each stack in a min_stack.
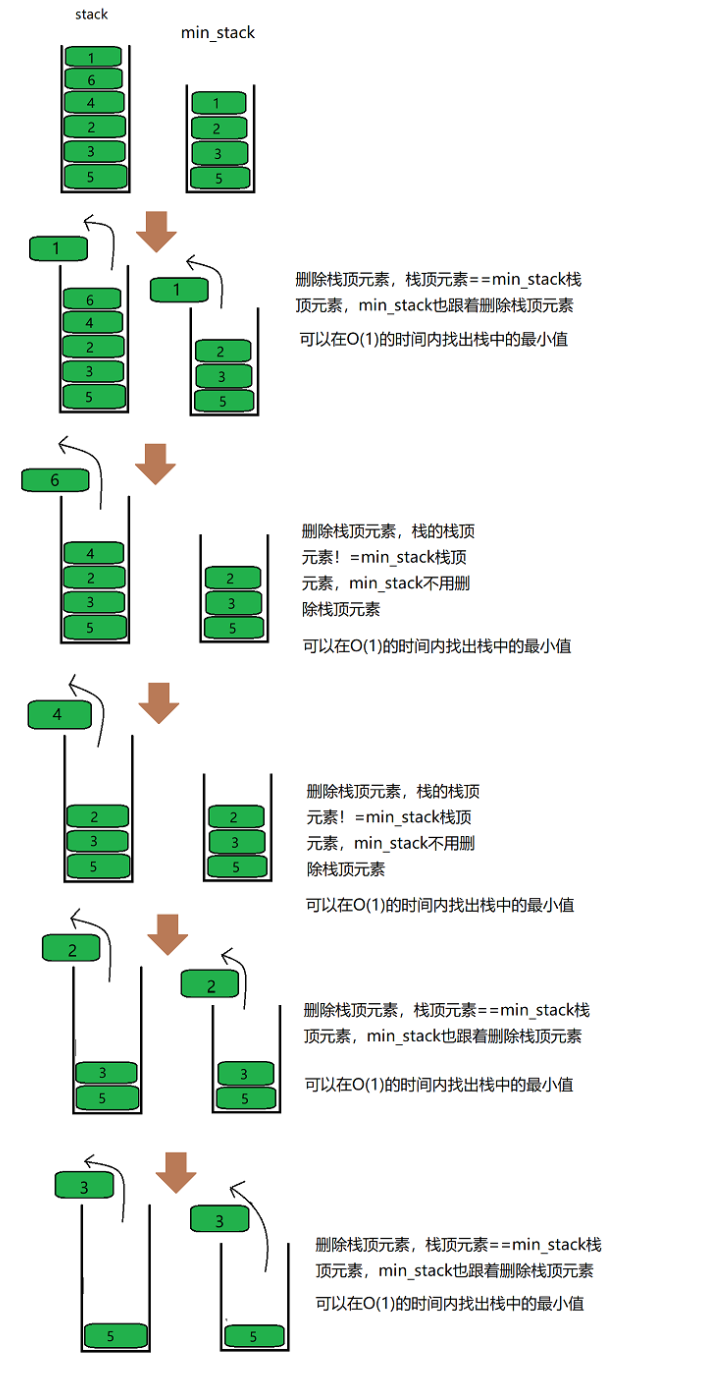
When the element at the top of the stack is deleted, min_stack also deletes the top element of the stack, ensuring the minimum value and min of the elements in the stack_ Stack corresponds to min directly when finding the minimum value in the stack_ Take it from the top of the stack. The time complexity is O(1), which is called exchanging space for time.

code:

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {}
    
    void push(int val) {
        st.push(val);
        if(min_stack.empty()||val<=min_stack.top())
        min_stack.push(val);
        else
        {
            min_stack.push(min_stack.top());
        }
    }
    
    void pop() {     
        st.pop();
        min_stack.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int getMin() {
        return min_stack.top();
    }
    private:
        stack<int> st;
        stack<int> min_stack;
};

Optimization problem solution 1

In the above method, there is a waste of space.
For example: {5, 3, 2, 4, 6, 1}
In Min_ The stack also stores {5, 3, 2, 2, 2, 1}. When entering the stack 4 and 6, it should also be in min_ 2 is stored in stack, resulting in a certain degree of space waste.
Is there any good solution? If only we could avoid it. 🧐
When the element on the stack is smaller than min_ When the element at the top of the stack is large, min_stack does not need to save the minimum value in the stack.
Only the elements on the stack are better than min_ When the element at the top of the stack is small or equal to, the minimum value in the stack needs to be saved.
For example: {5, 3, 2, 4, 6, 1}
1: 5 when entering the stack, the current minimum value is 5, min_stac is saved for 5 min_ Only 5 in stack: {5}
2: 3 when entering the stack, the current minimum value is 3, min_stac is saved for 3 min_ Only 5 in stack: {5, 3}
3: 2 when entering the stack, the current minimum value is 2, min_stac is saved for 2 min_ Only 5 in stack: {5, 3, 2}
4: 4 when entering the stack, the current minimum value is 2. There is no need to save the minimum value at this time. At this time, min_ Only 5 in stack: {5, 3, 2}
5: 6 when entering the stack, the current minimum value is 2. There is no need to save the minimum value at this time. At this time, min_ Only 5 in stack: {5, 3, 2}
6: 1 when entering the stack, the current minimum value is 1, min_stac save for 1 min_ Only 5 in stack: {5, 3, 2, 1}
When deleting the stack top element, when the stack top element and min_ If the stack top elements are the same, min_ The stack top element is also deleted. Different time, min_stack top element does not need to be deleted.

code:

class MinStack {
public:
    /** initialize your data structure here. */

    MinStack() {}
    
    void push(int val) {
        st.push(val);
        if(min_stack.empty()||val<=min_stack.top())
        min_stack.push(val);
    }
    
    void pop() {
        if(st.top()==min_stack.top())
        {
            min_stack.pop();
        }
        st.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int getMin() {
        return min_stack.top();
    }
    private:
    	stack<int> st;
    	stack<int> min_stack;
};

Optimization problem solution 2

There will also be a waste of space in optimization problem solution 1.
For example: {5, 3, 2, 2, 2, 6, 4, 1, 1, 1}
Use the method in optimization problem solution 1: min_stack: {5, 3, 2, 2, 2, 1, 1, 1}, duplicate 2 and 1 appear.
If there are extreme cases and N 2's occur, then in min_stack also needs to store N 2, which wastes a lot of space.
Is there any way to solve this problem? 🧐
Counting method: the same principle as counting sorting.
For example: {5, 3, 2, 2, 2, 6, 4, 1, 1, 1}
Use a structure to record:

struct val_count
{
	int _val;//Record minimum
	int _count://Recording times
};

In min_stack: {5,1}, {3,1}, {2,3}, {1,3} --- > the previous number represents the minimum value of this stage, and the following number represents the number of occurrences of the minimum value of this stage.

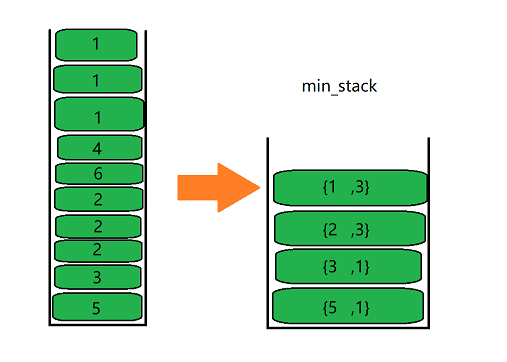
Until_ The Min is deleted only when the count is reduced to 0_ Stack top element.

code:

struct val_count
{
    int _val;
    int _count;
};
class MinStack {
public:
    /** initialize your data structure here. */
    
    MinStack() {}
    
    void push(int val) {
        st.push(val);
        if(min_stack.empty()||val<(min_stack.top()._val))
        {
           vat_count temp={val,1};
           min_stack.push(temp);
        }
        else
        {
            if(val==(min_stack.top()._val))
            min_stack.top()._count++;
        }
    }
    
    void pop() {
        if(st.top()==min_stack.top()._val)
        {
            min_stack.top()._count--;
            if(min_stack.top()._count==0)
            min_stack.pop();
        }
        st.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int getMin() {
        return min_stack.top()._val;
    }

    private:
        stack<int> st;
        //stack<int> min_stack;
        stack<vat_count> min_stack;
};

That's it