Original question link
General idea of the topic
On a map
n
(
2
≤
n
≤
100
)
n(2\le n\le 100)
n(2 ≤ n ≤ 100) points, each point corresponds to a coordinate:
x
(
−
10000
≤
x
≤
10000
)
,
y
(
−
10000
≤
y
≤
10000
)
x\ (-10000\le x\le 10000),y\ (-10000\le y\le 10000)
x (−10000≤x≤10000),y (−10000≤y≤10000)
Give again
m
(
1
≤
m
≤
n
2
−
n
2
)
m\ (1\le m\le \frac{n^2-n}2)
M (1 ≤ m ≤ 2n2 − n) edges (each edge corresponds to two numbers, representing the first point and the second point in the connected side respectively), and an initial position and an end position (second position)
1
≤
s
≤
n
1\le s\le n
1 ≤ s ≤ n points and
1
≤
t
≤
n
1\le t\le n
1 ≤ t ≤ n points). Find the shortest path from the initial position to the end position.
Problem solving ideas
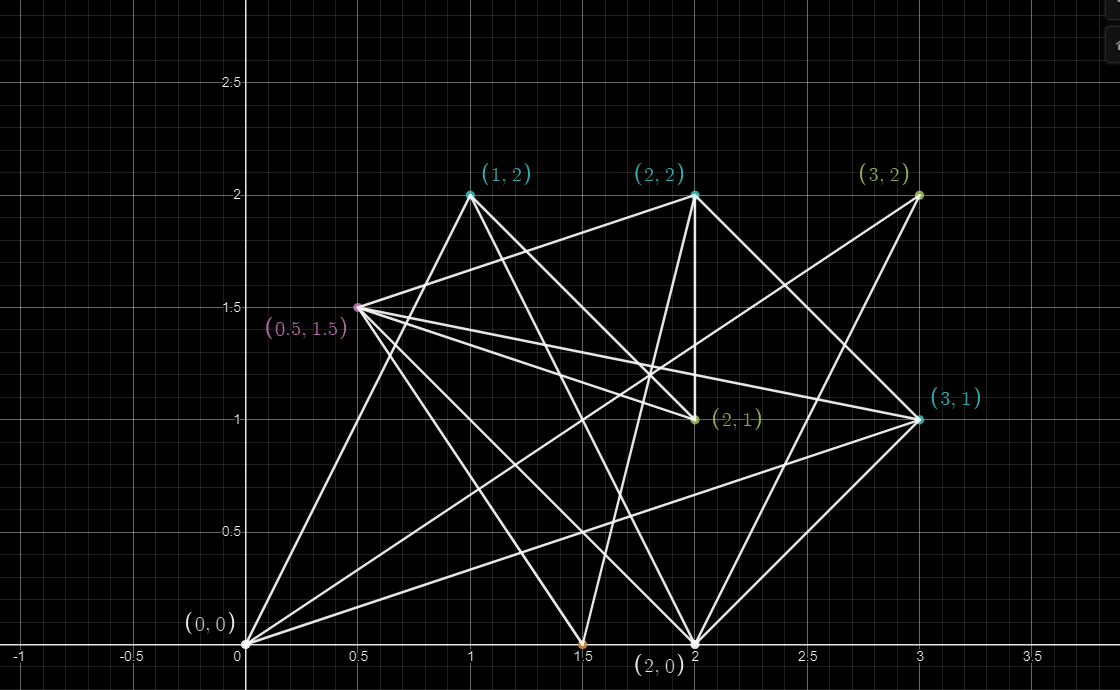
Floyed warhall algorithm
This algorithm is a dynamic programming algorithm. The main processes are:
1. Find an initial point:
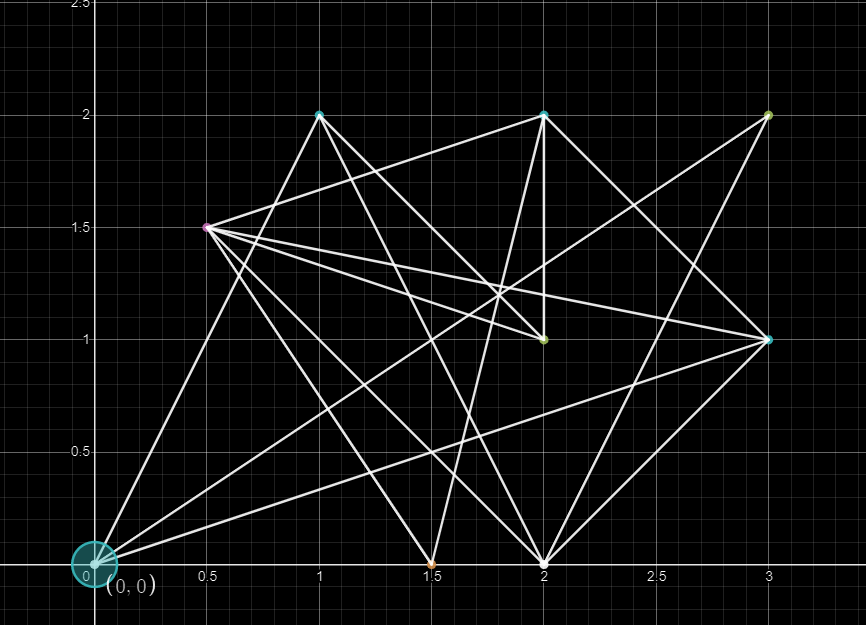
2. Find an end point:
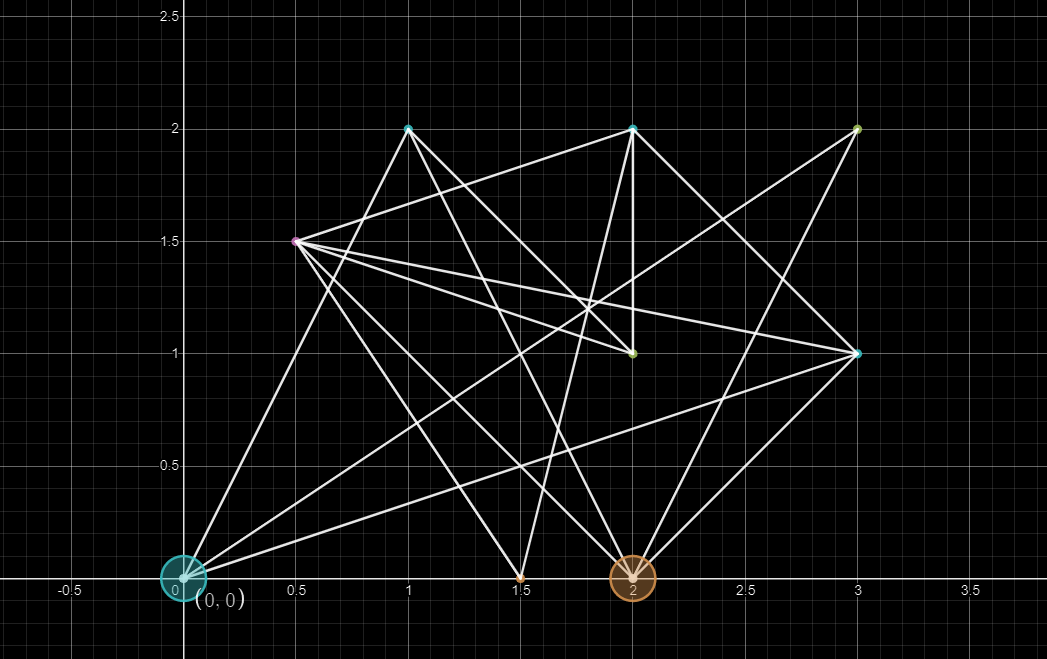
3. Find a transit point and try to transit. Compare the distance connected through this point with the original shortest distance and select a shorter path:
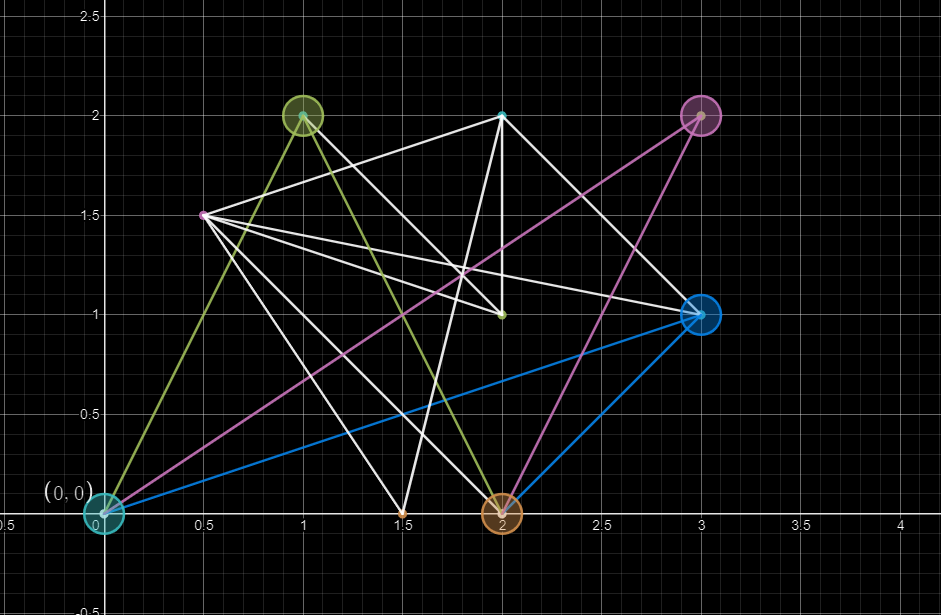
code implementation
#include<iostream>
#include<fstream>
#include<set>
#include<map>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
struct node{
double x,y;
} xy[1010];
double a[1010][1010];
int f,t,n,m;
double dis(double x_1,double y_1,double x_2,double y_2)
{
return sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2));//Using Pythagorean theorem to calculate straight line distance
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>xy[i].x>>xy[i].y;
cin>>m;
memset(a,0x5f,sizeof(a));
for(int i=1;i<=m;i++){
cin>>f>>t;
double d=dis(xy[f].x,xy[f].y,xy[t].x,xy[t].y);//Distance between two straight lines
a[f][t]=d;//Establish edge
a[t][f]=d;//Establish edge
}
cin>>f>>t;//Enter start and end points
for(int k=1;k<=n;k++){//Enumerate transit points
for(int i=1;i<=n;i++){//Enumeration starting point
for(int j=1;j<=n;j++){//Enumeration end point
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);//Step 3: relaxation operation
}
}
}
printf("%.2f",a[f][t]);//Shortest circuit from f to t
}
Dijkstra algorithm
The idea of this algorithm is similar to greed. Each time, find the shortest edge from the existing edges and spread outward, and update each edge connected to it. The specific process is as follows:
1. Find the shortest edge
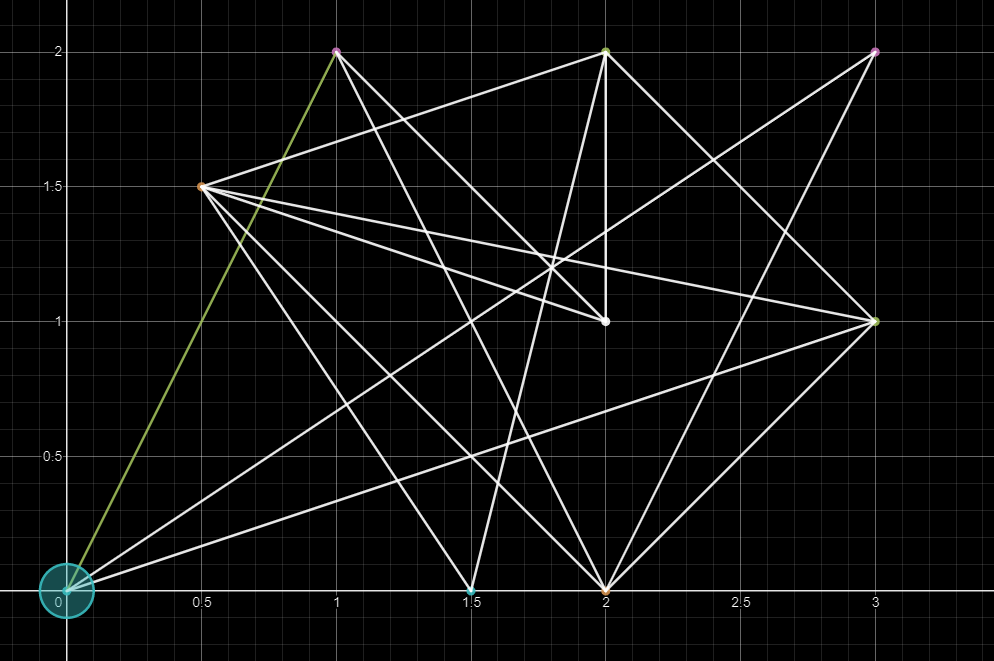
2. Update the shortest path
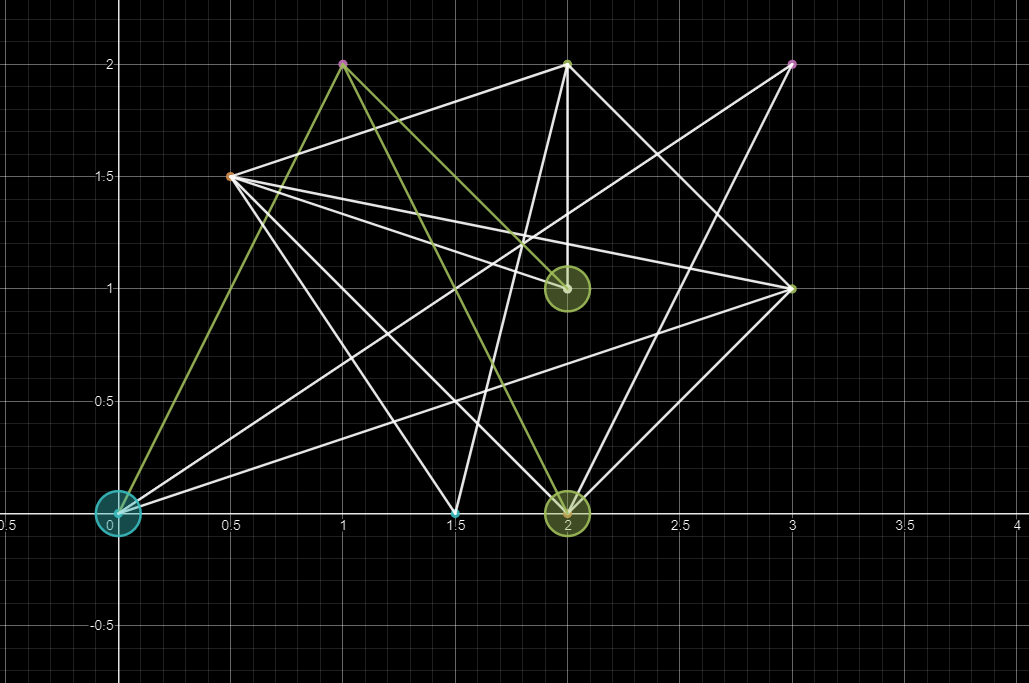
#include<iostream>
#include<fstream>
#include<set>
#include<map>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
struct node{
double x,y;
} xy[110];
struct node2{
double _dis;
int x;
};
double n,m,Min[110],a[110][110];
int f,t;
bool v[110];
double dis(double x_1,double y_1,double x_2,double y_2)
{
return sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2));//Using Pythagorean theorem to calculate straight line distance
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>xy[i].x>>xy[i].y;
cin>>m;
memset(a,0x7f,sizeof(a));
for(int i=1;i<=m;i++){
cin>>f>>t;
double d=dis(xy[f].x,xy[f].y,xy[t].x,xy[t].y);//Distance between two straight lines
a[f][t]=d;//Establish edge
a[t][f]=d;//Establish edge
}
memset(Min,0x7f,sizeof(Min));
memset(v,true,sizeof(v));
cin>>f>>t;
Min[f]=0;
int next;
for(int i=1;i<=n;i++){
next=0;
for(int j=1;j<=n;j++){//Enumerate shortest paths
if(Min[j]<Min[next]&&v[j])
next=j;//record
}
if(next==0)//Unable to update
break;
v[next]=false;//Mark as final answer
for(int j=1;j<=n;j++){
if(Min[j]>a[next][j]+Min[next]&&v[j])//Update length, relax operation
Min[j]=a[next][j]+Min[next];//Update length, relax operation
}
}
printf("%.2f",Min[t]);
return 0;
}
However, the time complexity of the above code is very high O ( n 2 ) O(n^2) O(n2) . One of them n n n is used to find the shortest path. If it can be omitted, the efficiency will be greatly improved. Here, we can use the priority queue.
Queue optimization, code implementation
#include<iostream>
#include<fstream>
#include<set>
#include<map>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
struct node{
double x,y;
} xy[110];
struct node2{
double _dis;
int x;
};
double n,m,Min[1010];
vector<node2> a[1010];
priority_queue<node2> q;//Finite queue, default large root heap
int f,t;
double dis(double x_1,double y_1,double x_2,double y_2)
{
return sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2));//Using Pythagorean theorem to calculate straight line distance
}
bool operator<(node2 q,node2 h)//Overload comparison symbol, double keyword comparison
{
if(q._dis!=h._dis)//First keyword
return q._dis<h._dis;
return q.x<h.x;//Second keyword
}
bool operator>(node2 q,node2 h)
{
if(q._dis!=h._dis)//First keyword
return q._dis>h._dis;
return q.x>h.x;//Second keyword
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>xy[i].x>>xy[i].y;
cin>>m;
for(int i=1;i<=m;i++){
cin>>f>>t;
double d=dis(xy[f].x,xy[f].y,xy[t].x,xy[t].y);//Distance between two straight lines
a[f].push_back((node2){d,t});//Establish edge, adjacency list
a[t].push_back((node2){d,f});//Establish edge, adjacency list
}
memset(Min,0x7f,sizeof(Min));
cin>>f>>t;
q.push((node2){0,f});//Initialize queue
Min[f]=0;//Initialization, the shortest path distance at the starting point is 0
while(!q.empty()){
int now_x=q.top().x;
double now_dis=-q.top()._dis;//Remove element from team leader
q.pop();
if(Min[now_x]<now_dis) continue;
for(int i=0;i<a[now_x].size();i++){//Traversal adjacency list
int next=a[now_x][i].x;
if(Min[next]>now_dis+a[now_x][i]._dis){//Update length, relax operation
Min[next]=now_dis+a[now_x][i]._dis;//Update length, relax operation
q.push((node2){-Min[next],next});//Update the priority queue, multiply by - 1 when storing, and sort by using the large root heap
}
}
}
printf("%.2f",Min[t]);
return 0;
}
spfa algorithm
This algorithm is similar to breadth search, but allows each point to enter the queue repeatedly, but does not allow one point to have two points in the queue at the same time. The specific methods are as follows:
1. Take an element from the team leader and update its collar
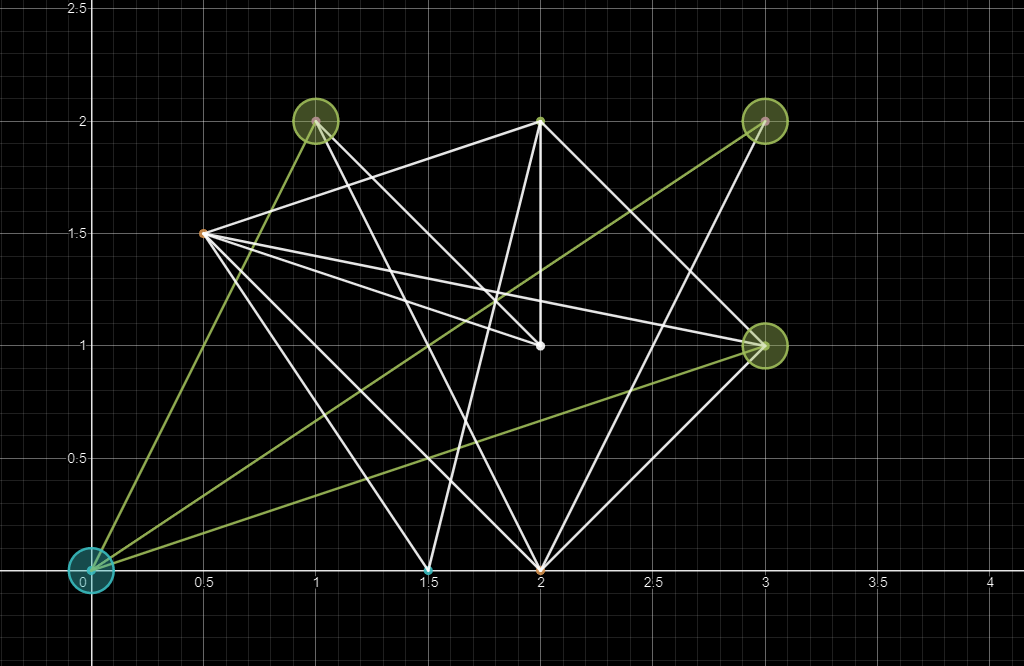
2. Select the point that is successfully updated and join the team
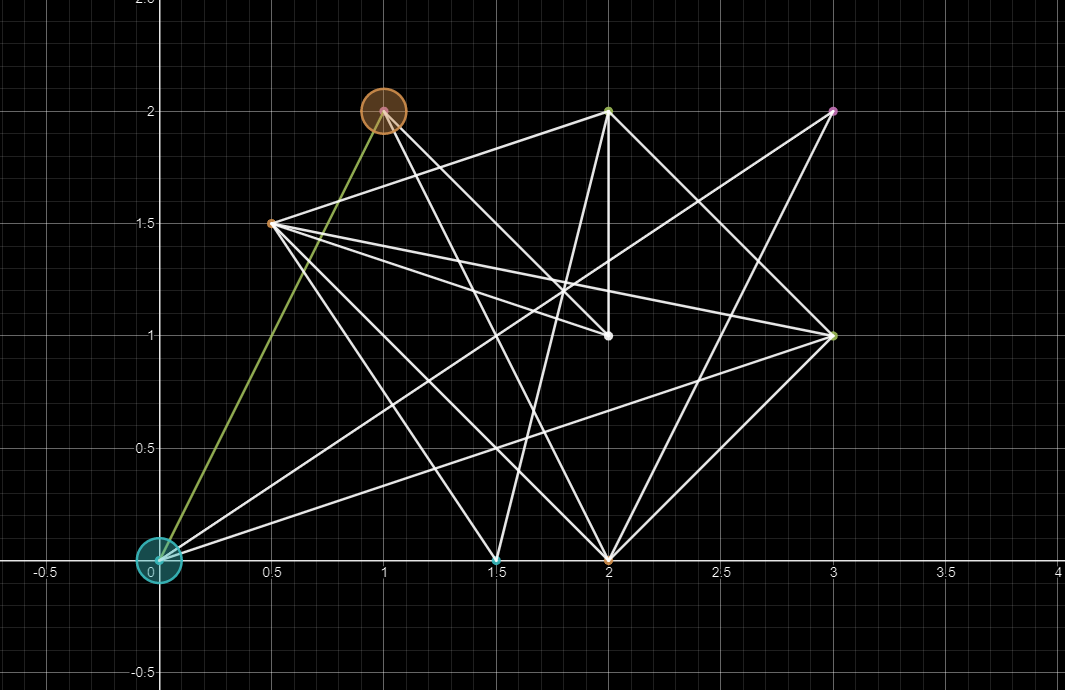
code implementation
#include<iostream>
#include<fstream>
#include<set>
#include<map>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
struct node{
double x,y;
} xy[1010];
struct node2{
int p;
double l;
};
vector<node2> a[1010];
bool v[1010];
int f,t,n,m;
double ans[1010];
int q[1010];
double dis(double x_1,double y_1,double x_2,double y_2)
{
return sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2));//Using Pythagorean theorem to calculate straight line distance
}
void work(int n2)
{
int h=0,t=0;
v[n2]=true;//Initialize tag queue
q[++t]=n2;//Initialize team leader element
ans[n2]=0;//Initialize the starting length of the shortest path
while(h!=t)
{
h=h%n+1;//Loop queue
int now=q[h];
for(int i=0;i<a[now].size();i++){//Traversal adjacency list
if(ans[now]+a[now][i].l<ans[a[now][i].p]){//Update length, relax operation
ans[a[now][i].p]=ans[now]+a[now][i].l;//Update length, relax operation
if(!v[a[now][i].p]){//Determine whether it is in the queue
t=t%n+1;//Loop queue
q[t]=a[now][i].p;//Join the team
v[a[now][i].p]=true;//Mark into the team
}
}
}
v[now]=false;//Get out of the team completely
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>xy[i].x>>xy[i].y;
ans[i]=0x7fffffff;
}
cin>>m;
for(int i=1;i<=m;i++){
cin>>f>>t;
double d=dis(xy[f].x,xy[f].y,xy[t].x,xy[t].y);//Distance between two straight lines
a[f].push_back((node2){t,d});//Establish edge, adjacency list
a[t].push_back((node2){f,d});//Establish edge, adjacency list
}
cin>>f>>t;
work(f);
printf("%.2f",ans[t]);
}
Sample
input
5 0 0 2 0 2 2 0 2 3 1 5 1 2 1 3 1 4 2 5 3 5 1 5
output
3.41