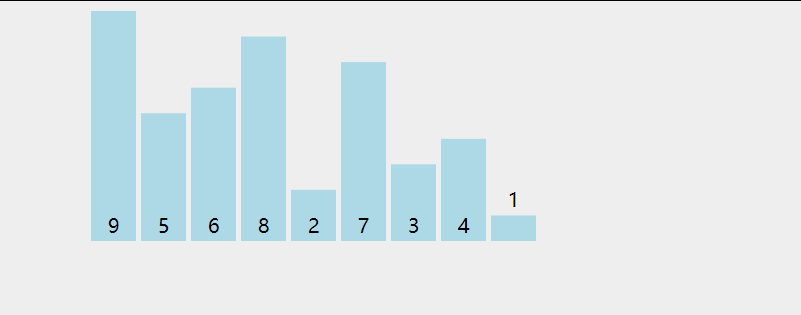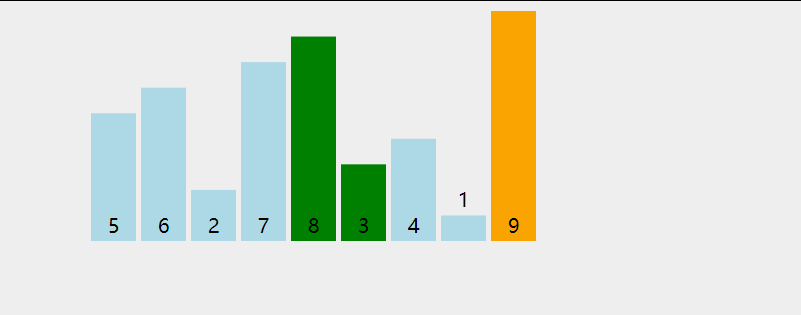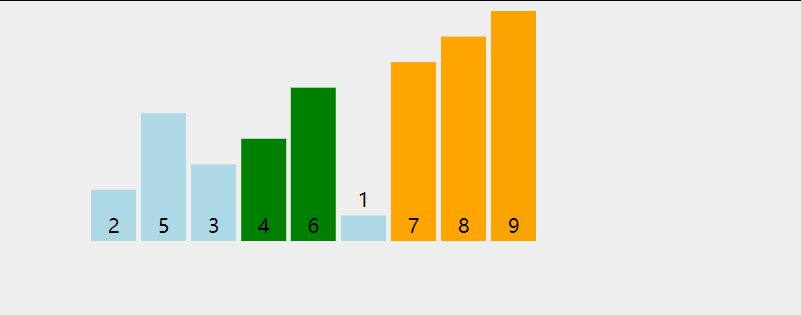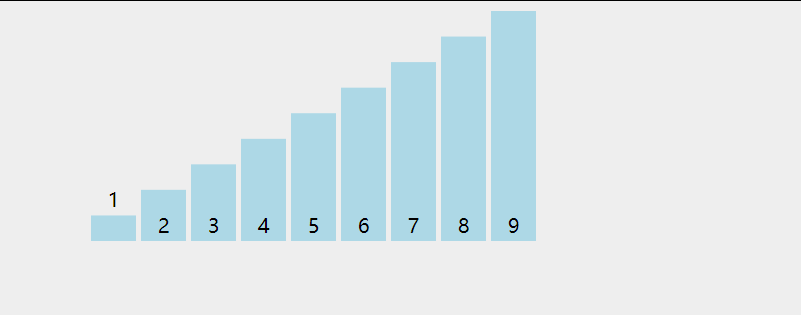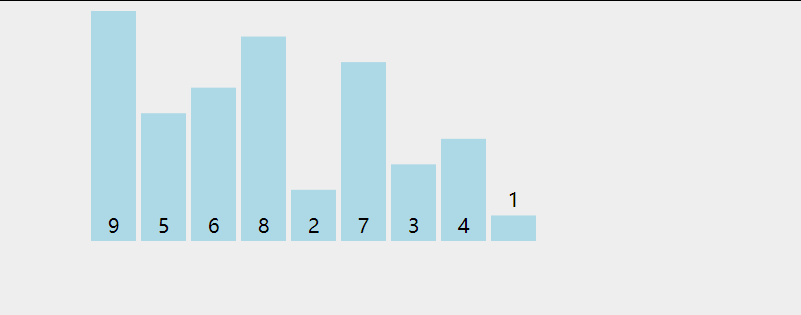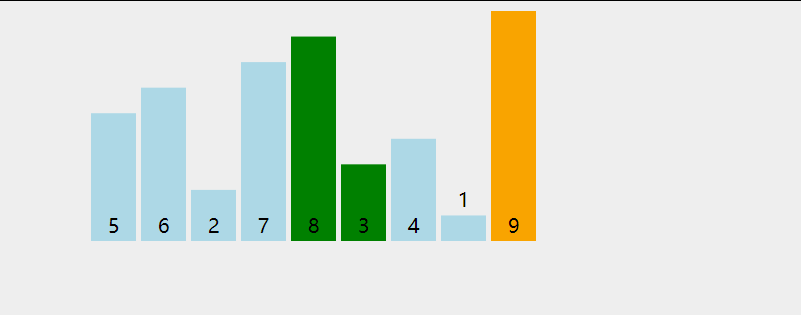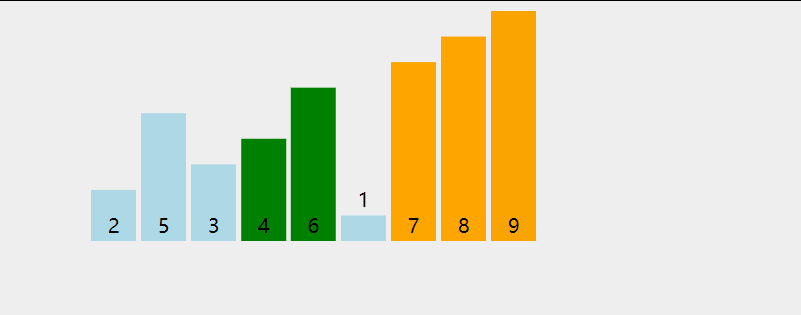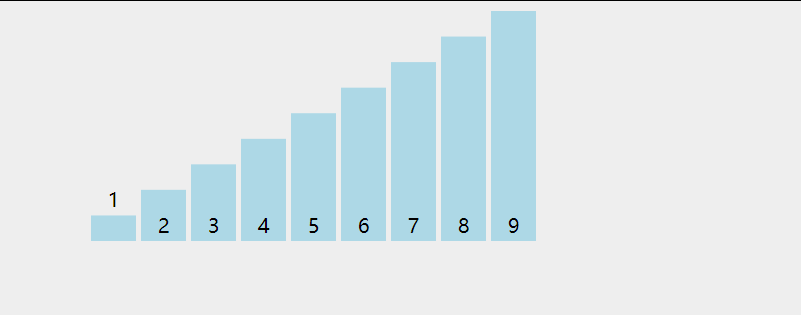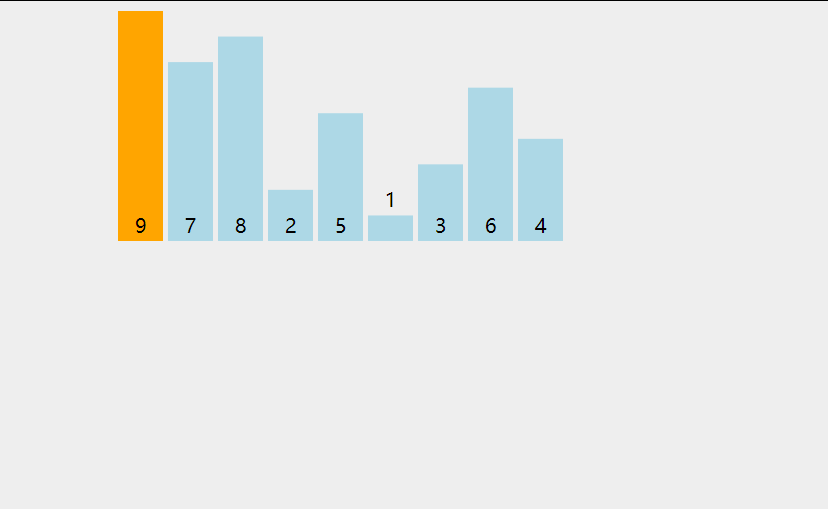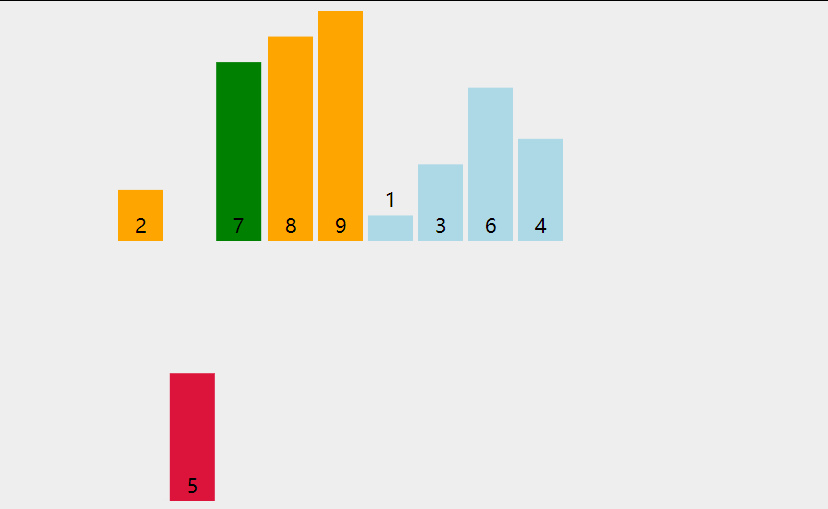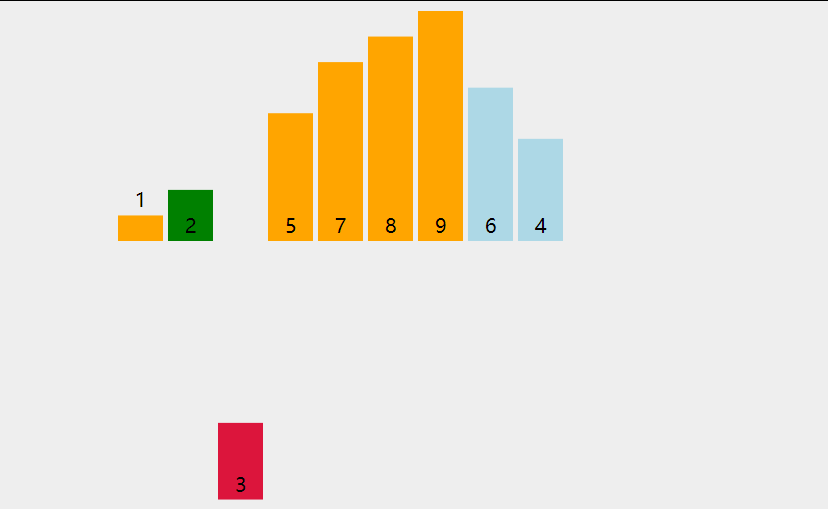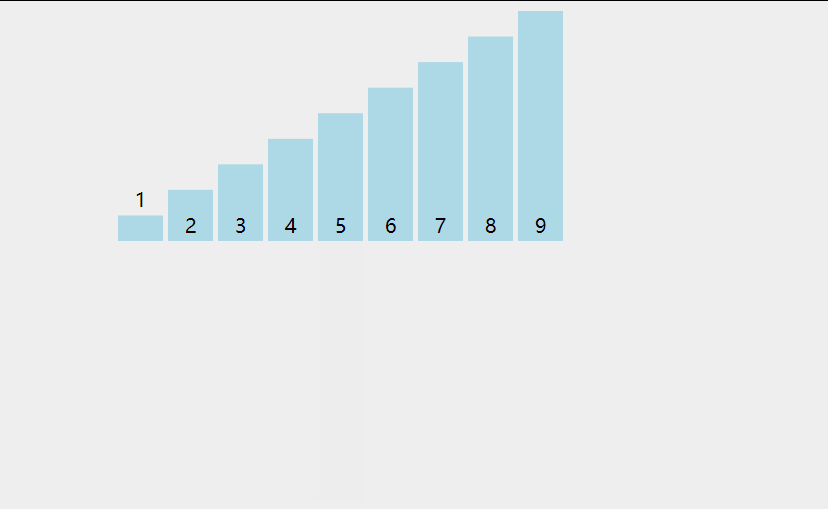JavaScript implementation of sorting algorithm

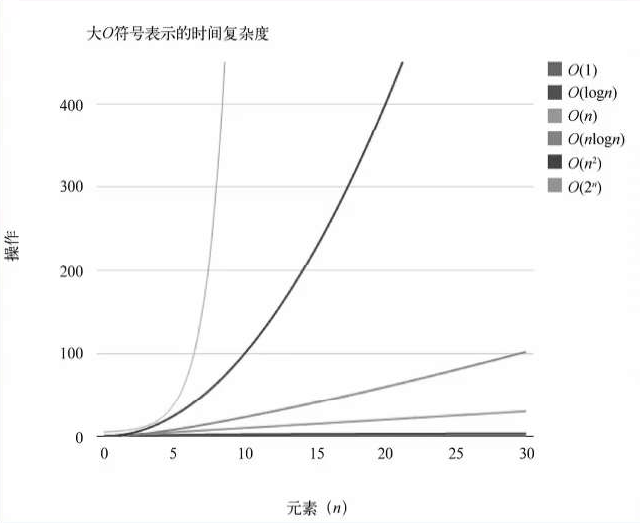
1, Large O representation

Large O notation:

• In the computer, a rough measure is used to describe the efficiency of computer algorithms. This method is called * * "Big O" representation**
• When the number of data items changes, the efficiency of the algorithm will also change. Therefore, algorithm A is twice as fast as algorithm B. such A comparison is meaningless.
• Therefore, we usually use how the speed of the algorithm changes with the amount of data to express the efficiency of the algorithm, and the large O representation is one of the ways.

Common large O representations

Symbol	name
O(1)	constant
O(log(n))	logarithm
O(n)	linear
O(nlog(n))	Linear and logarithmic product
O(n²)	square
O(2n)	index

Time complexity of different large O forms:

It can be seen that the efficiency is: O (1) > O (logn) > O (n) > O (nlog(n)) > O (n) ²)> O(2^n)

Three rules for deriving the large O representation:

• Rule 1: replace all addition constants in the running time with constant 1. For example, 7 + 8 = 15, use 1 to represent the operation result 15, and the large o representation is O (1);
• Rule 2: only the highest order term is reserved in the operation. For example, N^3 + 3n +1, the large o representation is O (N3);
• Rule 3: if the constant of the highest order term is not 1, it can be omitted. For example, 4N2, the large o representation is O (N2);

2, Sorting algorithm

Here we mainly introduce several simple sorting and advanced sorting:

• **Simple sort: * * bubble sort, select sort, insert sort;
• **Advanced sorting: * * Hill sorting and quick sorting;

Here, create a list class ArrayList and add some properties and methods to store these sorting methods:

    //Create list class
    function ArrayList() {
      //attribute
      this.array = []

      //method
      //Encapsulates the method of inserting data into an array
      ArrayList.prototype.insert = function(item){
        this.array.push(item)
      }

      //toString method
      ArrayList.prototype.toString = function(){
        return this.array.join('-')
      }

      //Exchange data between two locations
      ArrayList.prototype.swap = function(m, n){
        let temp  = this.array[m]
        this.array[m] = this.array[n]
        this.array[n] = temp
      }

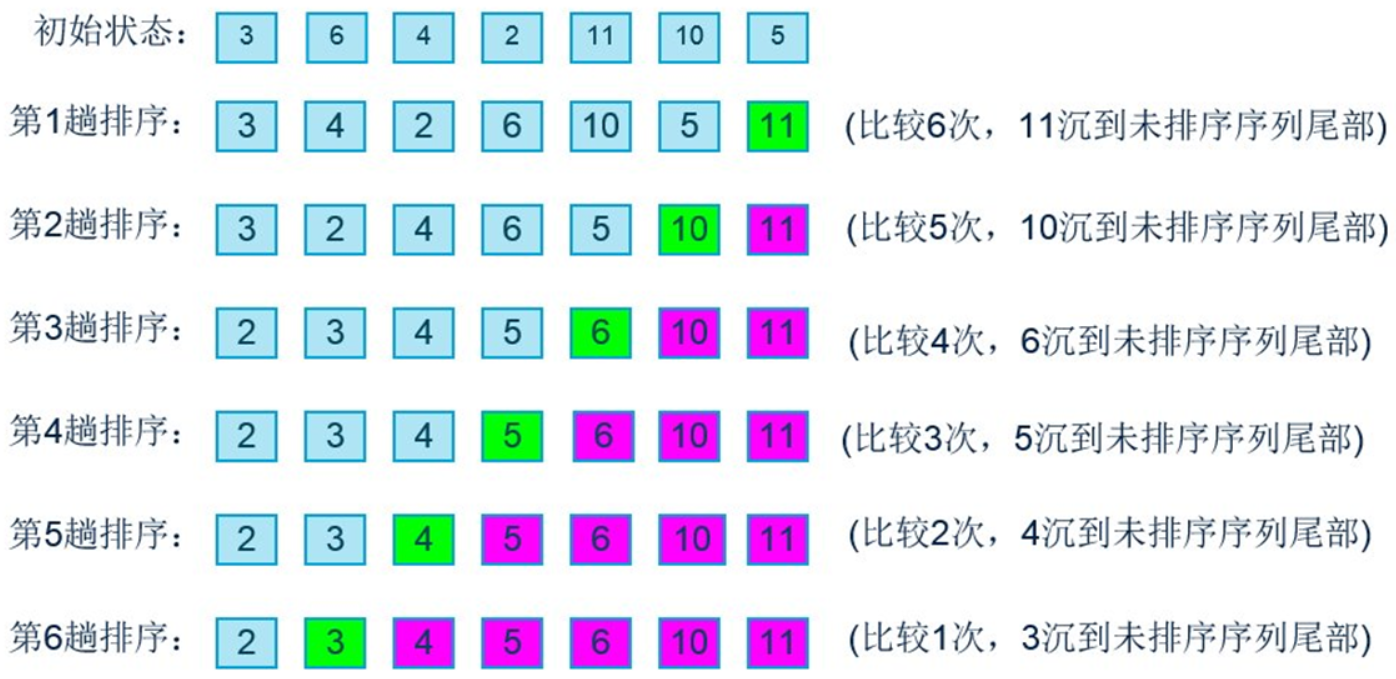
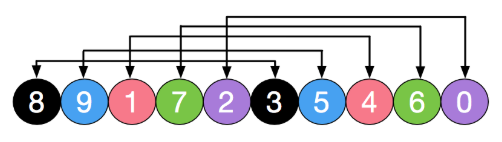
1. Bubble sorting

Bubble sorting idea:

• Compare the size relationship of two adjacent elements from beginning to end for each unordered element;
• If the person on the left is tall, they will exchange positions. For example, if 1 is shorter than 2, they will not exchange positions;
• Move one bit to the right, continue to compare 2 and 3, and finally compare length - 1 and length - 2 data;
• When reaching the far right, the tallest person must be placed on the far right;
• According to this idea, when starting from the leftmost end, you only need to go to the penultimate position;

Implementation idea:

Two layer cycle:

• Outer circulation control bubbling times:
  • First time: j = length - 1, compare to the penultimate position;
  • The second time: j = length - 2, compare to the penultimate position;
• The inner loop controls the number of comparisons per trip:
  • First comparison: i = 0, compare the two data at positions 0 and 1;
  • The last comparison: i = length - 2, compare length - 2 and length - 1 data;

The detailed process is shown in the figure below:

Dynamic process:

Code implementation:

      //Bubble sorting
      ArrayList.prototype.bubblesor = function(){
        //1. Get the length of the array
        let length = this.array.length

        //Outer circulation control bubbling times
        for(let j = length - 1; j >= 0; j--){
          //The inner loop controls the number of comparisons per trip
          for(let i = 0; i < j; i++){
          if (this.array[i] > this.array[i+1]) {
            //Exchange two data
            let temp  = this.array[i]
        	this.array[i] = this.array[i+1]
        	this.array[i+1] = temp
          }
        }
        }
      }

Test code:

    //Test class
    let list = new ArrayList()

    //Insert element
    list.insert(66)
    list.insert(88)
    list.insert(12)
    list.insert(87)
    list.insert(100)
    list.insert(5)
    list.insert(566)
    list.insert(23)
    
    //Verify bubble sort
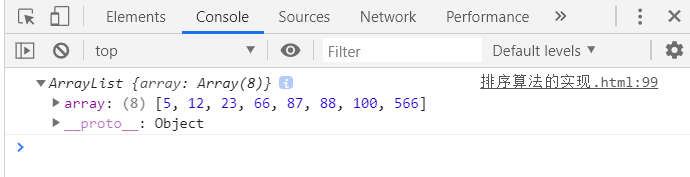
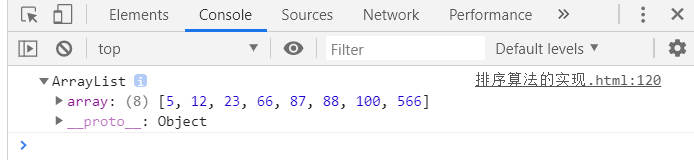
    list.bubblesor()
    console.log(list);

Test results:

Bubble sorting efficiency:

• For the 7 data items mentioned above, the comparison times are: 6 + 5 + 4 + 3 + 2 + 1;
• For N data items, the comparison times are: (N - 1) + (N - 2) + (N - 3) +... + 1 = N * (N - 1) / 2; if two comparisons are exchanged once, the exchange times are: N * (N - 1) / 4;
• The comparison times and exchange times expressed by the large o representation are o (n * (n-1) / 2) and O (n * (n-1) / 4) respectively. According to the three rules of the large o representation, they are reduced to o (N^2);

2. Select Sorting

Selective sorting improves bubble sorting:

• Reduce the number of exchanges from O (N^2) to o (N);
• However, the comparison times are still O (N^2);

Select the idea of sorting:

• Select the position of the first index, such as 1, and then compare it with the following elements in turn;
• If the subsequent element is less than the element at index 1, the position is exchanged to index 1;
• After a round of comparison, it can be determined that the element at the specified index 1 position at the beginning is the smallest;
• Then use the same method to compare the remaining elements one by one except index 1;
• It can be seen that when sorting is selected, the minimum value will be selected in the first round and the second small value will be selected in the second round until sorting is completed.

Implementation idea:

Two layer cycle:

• Index specified by outer loop control:
  • First time: j = 0, specify the first element;
  • Last time: j = length - 1, specify the last element;
• The inner loop is responsible for comparing the elements of the specified index (i) with the remaining elements (i - 1);

Dynamic process:

Code implementation:

      //Select sort
      ArrayList.prototype.selectionSort = function(){
        //1. Get the length of the array
        let length = this.array.length

        //2. Outer loop: get elements from 0
        for(let j = 0; j < length - 1; j++){
          let min = j
          //Inner loop: start from the i+1 position and compare with the following elements
        for(let i = min + 1; i < length; i++){
          if (this.array[min] > this.array[i]) {
            min = i
          }
        }
        this.swap(min, j)
        }
      }

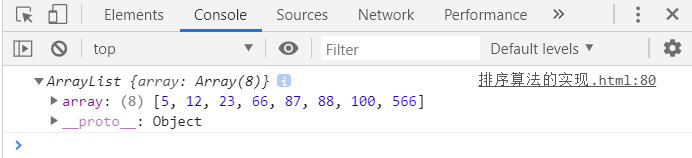
Test code:

    //Test class
    let list = new ArrayList()

    //Insert element
    list.insert(66)
    list.insert(88)
    list.insert(12)
    list.insert(87)
    list.insert(100)
    list.insert(5)
    list.insert(566)
    list.insert(23)
    
    //Verify selection sorting
    list.selectionSort()
    console.log(list);

Test results:

Select the efficiency of sorting:

• The comparison times of sorting selection are: N * (N - 1) / 2, expressed as O (N^2) in large o representation;
• The exchange times of sorting are: (N - 1) / 2, expressed as O (N) in large o representation;
• Therefore, the efficiency of selective sorting is higher than bubble sorting;

3. Insert sort

Insert sort is the most efficient sort in simple sort.

Insert the idea of sorting:

• The core of the idea of insertion sort is local order. As shown in the figure, the person on the left of X is called local order;
• First, specify a data X (starting from the first data) and turn the left side of data x into a locally ordered state;
• Then move X to the right by one bit. After reaching the local order again, continue to move X to the right by one bit and repeat the previous operation until X moves to the last element.

Detailed process of inserting sorting:

Dynamic process:

Code implementation:

      //Insert sort
      ArrayList.prototype.insertionSort = function(){
        //1. Get the length of the array
        let length = this.array.length

        //2. Outer loop: start from the second data and insert the locally ordered data on the left
        for(let i = 1; i < length; i++){
          //3. Inner loop: get the elements at position i, and use the while loop (key) to compare them with the local ordered data on the left
          let temp = this.array[i]
          let j = i
          while(this.array[j - 1] > temp && j > 0){
            this.array[j] = this.array[j - 1]//Big data shift right
            j--
          }
          //4. After the while loop ends, the data on the left of index = j becomes locally ordered and array[j] is the largest. At this time, reset array[j] to the data array[i] before sorting to facilitate the next for loop
          this.array[j] = temp
        }
      }

Test code:

   //Test class
    let list = new ArrayList()

    //Insert element
    list.insert(66)
    list.insert(88)
    list.insert(12)
    list.insert(87)
    list.insert(100)
    list.insert(5)
    list.insert(566)
    list.insert(23)
    // console.log(list);

    //Verify insert sort
    list.insertionSort()
    console.log(list);

Test results:

Efficiency of insert sort:

• **Comparison times: * * the maximum number of times required for the first pass is 1; the maximum number of times required for the second pass is 2; and so on, the maximum number of times required for the last pass is N-1; therefore, the total comparison times for insertion sorting is N * (N - 1) / 2; however, in fact, before the insertion point is found in each pass, only half of all data items need to be compared, so the comparison times are N * (N - 1) / 4;
• Exchange times: 0 times when the first data is specified as X, 1 times at most when the second data is specified as X, and so on. N - 1 times at most when the nth data is specified as X, so a total of N * (N - 1) / 2 times are required, and the number of draws is N * (N - 1) / 2;
• Although the efficiency of inserting sort represented by large O representation is also O (N^2), the overall operation times of inserting sort are less. Therefore, in simple sort, the efficiency of inserting sort is the highest;

4. Hill sort

Hill sort is an efficient improved version of insert sort, which is more efficient than insert sort.

Historical background of Hill sort:

• Hill sorting is named after its designer Donald Shell, and the algorithm was published in 1959;
• Hill's algorithm breaks through the barrier that the time complexity of * * algorithm is O (N^2) * * for the first time. In order to commemorate the milestone of the algorithm

Shell is used to name the algorithm;

Insert sorted questions:

• Suppose a small data item is located close to the right end, which should be the location of the larger data item;
• Move this small data item to the correct position on the left, and all intermediate data items must move one bit to the right, which is very inefficient;
• If in some way, the smaller data items can be moved to the left without moving all the intermediate data items one by one, the execution speed of this algorithm will be greatly improved.

Implementation idea of hill sorting:

• Hill sort mainly realizes quick sorting by grouping data;
• Divide the data into gap groups (the number of groups is equal to gap) according to the set increment (GAP), and then sort locally in each group;

If there are 10 data in an array, the first data is black and the increment is 5. Then the second black data index=5, and the third black data index = 10 (does not exist). Therefore, there are only 2 black data in each group, 10 / 2 = 5, which can be divided into 5 groups, that is, the number of groups is equal to the incremental gap.

• After sorting, decrease the increment, continue grouping, and perform local sorting again until the increment gap=1. Then you can sort the array only by fine tuning;

The specific process is as follows:

• Before sorting, the original array storing 10 data is:

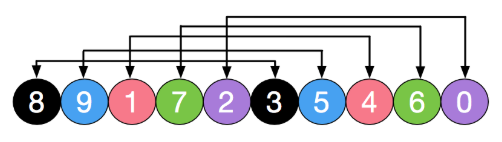
• Let the initial increment gap = length / 2 = 5, that is, the array is divided into 5 groups, as shown in the figure: [8,3], [9,5], [1,4], [7,6], [2,0]:

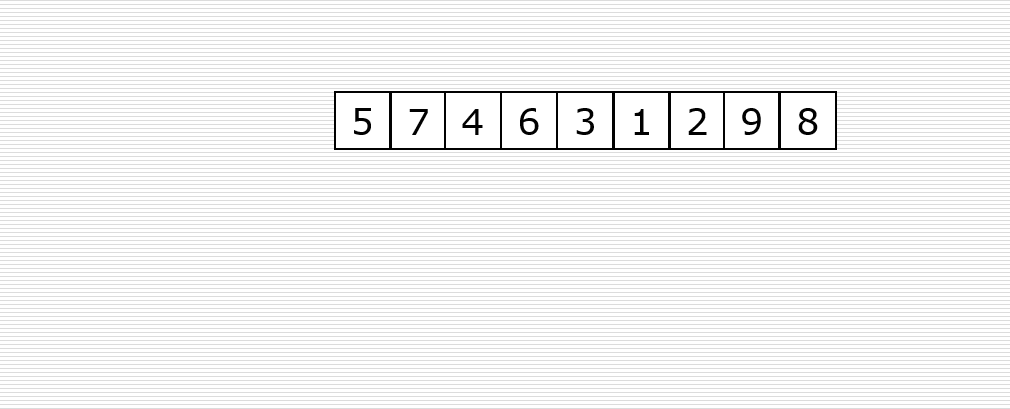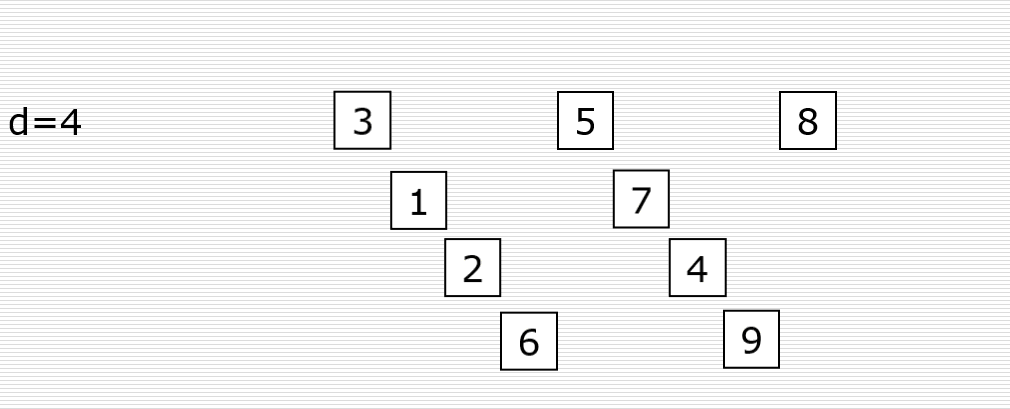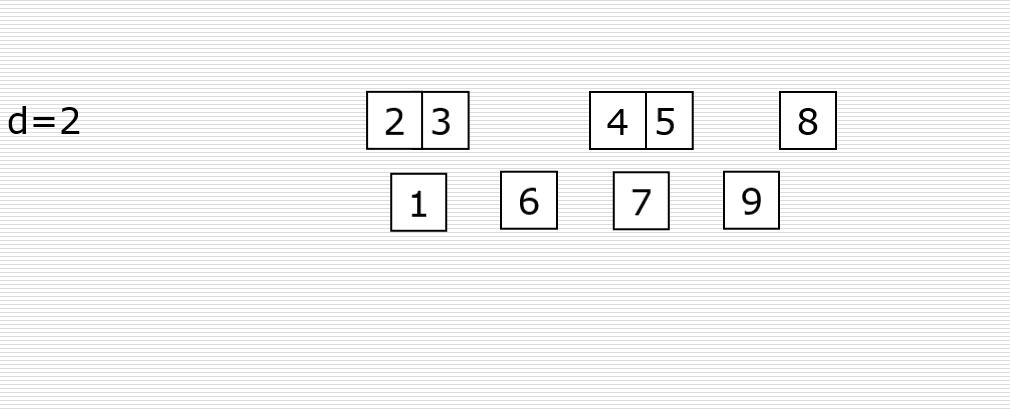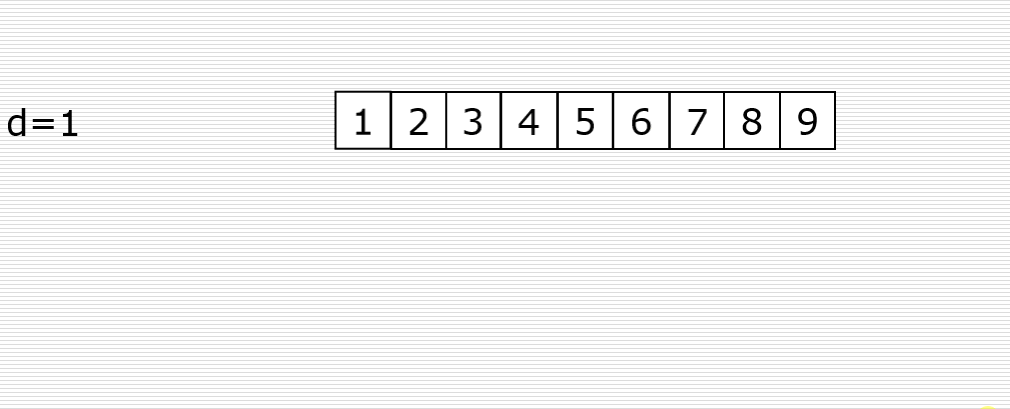
• Then sort the data locally in each group. The order of the five groups is as shown in the figure, which becomes: [3,8], [5,9], [1,4], [6,7], [0,2]:

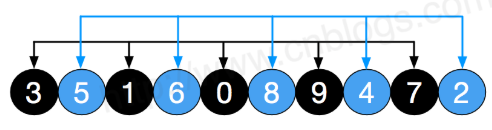
• Then reduce the increment gap = 5 / 2 = 2, that is, the array is divided into two groups, as shown in the figure: [3, 1, 0, 9, 7], [5, 6, 8, 4, 2]:

• Then sort the data locally in each group. The order of the two groups is as shown in the figure, which becomes: [0, 1, 3, 7, 9], [2, 4, 5, 6, 8]:

• Then reduce the increment gap = 2 / 1 = 1, that is, the array is divided into 1 groups, as shown in the figure: [0, 2, 1, 4, 3, 5, 7, 6, 9, 8]:

• Finally, you only need to insert and sort this group of data to complete the sorting of the whole array:

Dynamic process:

In the figure, d represents incremental gap.

Incremental selection:

• The initial spacing suggested by hill in the original is N / 2. For example, for an array with N = 100, the increment sequence is: 50, 25, 12, 6, 3, 1. It can be found that if it cannot be divided, it can be rounded down.
• **Hibbard incremental sequence: the incremental sequence algorithm is: 2^k - 1, i.e. 1, 3, 5, 7; The worst complexity of this case is O (N3/2) * *, and the average complexity is * * O (N5/4) * *, but it has not been proved;
• Sedgewcik incremental sequence:

The following code implementation uses the increment recommended in the Hill sort original, i.e. N / 2.

Code implementation:

      //Shell Sort 
      ArrayList.prototype.shellSort = function(){
        //1. Get the length of the array
        let length = this.array.length

        //2. Initialization increment
        let gap = Math.floor(length / 2)

        //3. The first layer of loop: while loop (to continuously reduce gap)
        while(gap >= 1 ){
          //4. Layer 2 loop: group with gap as increment, and insert and sort the groups
          //The key points are: take index = gap as the first selected data
          for(let i = gap; i < length; i++){
            let temp = this.array[i]
            let j = i
            //5. Third layer circulation: find the correct insertion position
            while(this.array[j - gap] > temp && j > gap - 1){
              this.array[j] = this.array[j - gap]
              j -= gap
            }
          //6. Set the element at position j to temp
          this.array[j] = temp
          }

          gap = Math.floor(gap / 2)
        }
      }

Here we explain the three-layer loop in the above code:

• **Layer 1 cycle: * * while cycle, which controls gap to decrease to 1;
• **Layer 2 cycle: * * take out the gap group data divided according to the g-increment gap respectively: take the data of index = gap as the first data selected, as shown in the figure below. If gap=5, the data of index = gap is 3, the data of index = gap - 1 is 8, and the two data are a group. Then, gap continues to add 1 and move to the right until gap < length. At this time, the array is divided into 5 groups.

• **Layer 3 cycle: * * insert and sort each group of data;

Test code:

   //Test class
    let list = new ArrayList()

    //Insert element
    list.insert(66)
    list.insert(88)
    list.insert(12)
    list.insert(87)
    list.insert(100)
    list.insert(5)
    list.insert(566)
    list.insert(23)
    // console.log(list);

    //Verify Hill sort
    list.shellSort()
    console.log(list);

Test results:

Efficiency of hill sorting:

• The efficiency of Hill sort is directly related to the increment. Even if the increment efficiency in the original is higher than that in simple sort.

5. Quick sort

Introduction to quick sort:

• Quick sorting can be said to be the fastest sorting algorithm among all sorting algorithms at present. Of course, no algorithm is optimal in any case. However, in most cases, quick sorting is a better choice.
• Quick sort is actually an upgraded version of bubble sort;

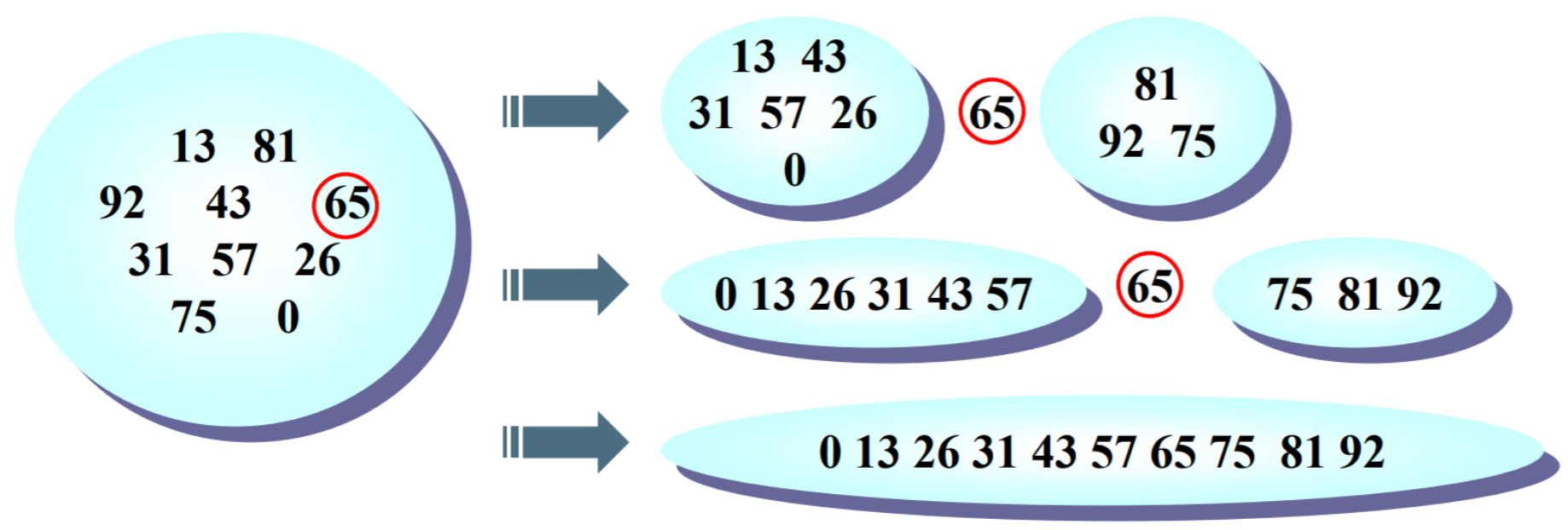
The core idea of quick sort is divide and conquer. First select a data (such as 65), put the smaller data on its left and the larger data on its right. This data is called a hub

Different from bubble sorting:

• The 65 we selected can be placed in the most correct position at one time, and then there is no need to move;
• For bubble sorting, even if the maximum value has been found, you need to continue to move the maximum value until it is moved to the far right;

Quick sort hub:

• **The first scheme: * * directly select the first element as the hub. However, when the first element is the minimum value, the efficiency is not high;
• **The second scheme: * * use random numbers. Random number itself is very performance consuming and is not recommended;
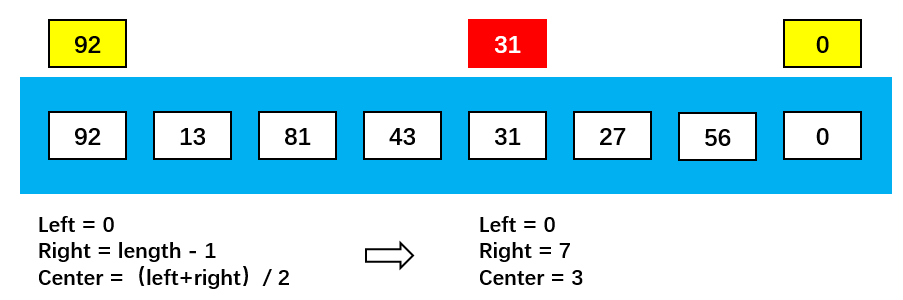
• Excellent solution: take index as the median after sorting the three data of header, median and bit; As shown in the figure below, the three data taken out according to the subscript value are: 92, 31, 0. After sorting, they become: 0, 31, 92. Take the median 31 as the hub (when (length-1) / 2 is not divided, it can be rounded down or up):

Realize hub selection:

//Exchange data between two locations
let swap = function(arr, m, n){
    let temp  = arr[m]
    arr[m] = arr[n]
    arr[n] = temp
}

//Quick sort
//1. Select hub
let median = function(arr){
  //1. Take out the middle position
  let center = Math.floor(arr.length / 2)
  let right = arr.length - 1 
  let left = 0

  //2. Determine the size and exchange
  if (arr[left] > arr[center]) {
    swap(arr, left, center)
  }
  if (arr[center] > arr[right]){
    swap(arr, center, right)
  }
  if (arr[left] > arr[right]) {
    swap(arr, left, right)
  }
  //3. Return to the hub
  return center
}

After obtaining the pivot function of the array, the data positions corresponding to the selected three subscript values become:

Dynamic process:

Quick sort code implementation:

//2. Quick sort
let QuickSort = function(arr){
  if (arr.length == 0) {
    return []
  }
  let center = median(arr)
  let c = arr.splice(center, 1)
  let l = []
  let r = []

  for (let i = 0; i < arr.length; i++) {
      if (arr[i] < c) {
        l.push(arr[i])
      }else{
        r.push(arr[i])
      }        
  }
  return QuickSort(l).concat(c, QuickSort(r))
}

The subtlety of the algorithm is through:

QuickSort(l).concat(c, QuickSort(r))

The QuickSort function is called recursively to sort the data l on the left and the data r on the right of the hub Center;

Test code:

let arr = [0, 13, 81, 43, 31, 27, 56, 92]
console.log(QuickSort(arr));

test result

Quicksort efficiency:

• Worst case efficiency of quick sort: each selected hub is the leftmost or rightmost data. At this time, the efficiency is equivalent to bubble sort, and the time complexity is O (n2). This situation can be avoided according to different hub options;
  (arr[i])
  }else{
  r.push(arr[i])
  }
  }
  return QuickSort(l).concat(c, QuickSort®)
  }

The subtlety of the algorithm is through:

QuickSort(l).concat(c, QuickSort®)

Recursive call`QuickSort`Function implements the hub`Center`Left data`l`And right data`r`Sorting of;

**Test code:**

let arr = [0, 13, 81, 43, 31, 27, 56, 92]
console.log(QuickSort(arr));

**test result**

[[External chain picture transfer...(img-WtBBEz39-1638750821889)]](https://gitee.com/ahuntsun/BlogImgs/raw/master / data structure and algorithm / sorting algorithm / 28.png)

**Quicksort efficiency:**

- Worst case efficiency of quick sorting: each selected hub is the leftmost or rightmost data. At this time, the efficiency is equivalent to bubble sorting, and the time complexity is**O(n2)**. This situation can be avoided according to different hub options;
- Average efficiency of quick sort:**O(N\*logN)**，Although the efficiency of other algorithms can also be achieved O(N*logN)，But quick sort is**first-class**.