1. Problem Description:
A magic square of k x k refers to a square matrix filled with integers, and the sum of each row, column and two diagonals are all equal. Integers in magic squares do not need to be different from each other. Obviously, every square of , 1 x 1 , is a magic square.
Give you an integer matrix of ^ m x n ^ grid. Please return the size of the largest magic square in the matrix (i.e. side length k).
Example 1:
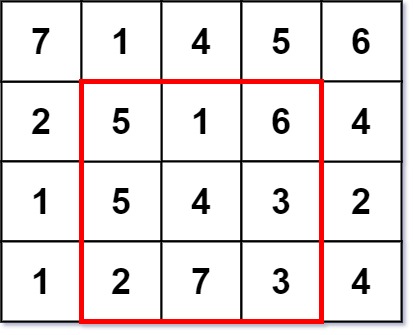
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: the maximum magic square size is 3.
The sum of each row, column and two diagonals is equal to 12.
-Sum of each line: 5 + 1 + 6 = 5 + 4 + 3 = 2 + 7 + 3 = 12
-Sum of each column: 5 + 5 + 2 = 1 + 4 + 7 = 6 + 3 + 3 = 12
-Sum of diagonal lines: 5 + 4 + 3 = 6 + 4 + 2 = 12
Example 2:
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: the maximum magic square size is 3.
The sum of each row, column and two diagonals is equal to 12.
-Sum of each line: 5 + 1 + 6 = 5 + 4 + 3 = 2 + 7 + 3 = 12
-Sum of each column: 5 + 5 + 2 = 1 + 4 + 7 = 6 + 3 + 3 = 12
-Sum of diagonal lines: 5 + 4 + 3 = 6 + 4 + 2 = 12
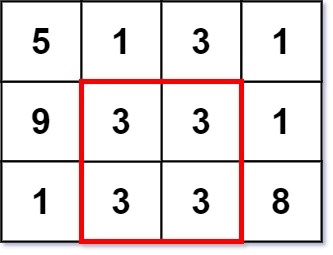
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2
Tips:
m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10 ^ 6
Source: LeetCode
Link: https://leetcode-cn.com/problems/largest-magic-square
2. Train of thought analysis:
By analyzing the topic, we can know that violent enumeration is the easiest to think of. Combined with the data range of the topic m, n = 50, the approximate total data scale is: 50 * (50 ^ 2) * (50 ^ 2) = 31250000, and it is not enumerated 50 times every time, so it should be acceptable. We can enumerate the length of l, l - 1, l - 2 When enumerating all square matrices of 1, we can enumerate the length from large to small, so that when we find a satisfactory answer, we can directly return the length of the square matrix. The outermost loop represents the length of the current square array, the second loop represents the starting row of the square array with the current length of l, and the third loop represents the starting column of the square array with the current length of l. in enumerating each square array with the length of l, calculate the sum of each row, the sum of each column, the sum of the main diagonal and the sub diagonal, s1, s2 calculate the sum of each row and column in the square array, It is necessary to set whether the sum of rows and columns of the current square array meets the criteria r_flag, c_flag is used to determine whether the sum of rows and columns is equal. Mainly pay attention to the details.
3. The code is as follows:
from typing import List
class Solution:
def largestMagicSquare(self, grid: List[List[int]]):
r, c = len(grid), len(grid[0])
max_l = min(r, c)
# Traversal in reverse order means enumerating from large to small
for l in range(max_l, 0, -1):
start_r, start_c = 0, 0
while start_r + l <= r:
start_c = 0
while start_c + l <= c:
# Enumerate each magic square and set two flags r_flag, c_flag to judge whether the sum of rows and columns of the current square matrix meets the conditions
r_flag, c_flag = True, True
r_s = -1
for j in range(start_r, start_r + l):
s1 = 0
for k in range(start_c, start_c + l):
s1 += grid[j][k]
if r_s == -1:
r_s = s1
elif r_s != s1:
r_flag = False
break
# The sum of columns is checked only if the sum of rows meets the conditions
if r_flag:
c_s = -1
for k in range(start_c, start_c + l):
s2 = 0
for j in range(start_r, start_r + l):
s2 += grid[j][k]
if c_s == -1:
c_s = s2
elif c_s != s2:
c_flag = False
break
if s1 == s2 and c_flag:
t1, t2 = 0, 0
# Start column position
t_c = start_c
for j in range(start_r, start_r + l):
t1 += grid[j][t_c]
t_c += 1
# Start line position
t_r = start_r
for j in range(start_c + l - 1, start_c - 1, -1):
t2 += grid[t_r][j]
t_r += 1
# The condition is satisfied only when the sum of the three is equal
if s1 == t1 and t1 == t2:
return l
start_c += 1
start_r += 1
return 1