The so-called 2-SAT problem is that there are two SAT problems (errors)

SAT is the abbreviation of well posedness problem. The general form is k - well posedness problem, which is abbreviated as k-SAT. And when k > 2 k>2 k> At 2, the problem is NP complete. So we only study k = 1 k > 2 k>2 k> 2.

1, 2-definition of SAT problem:

2-SAT, in short, gives n n n sets, each set has two elements, and several are known < a , b > <a,b> < A, b >, indicates a a a and b b b contradiction (among them) a a a and b b b belongs to different sets). Then select an element from each set to judge whether it can be selected together n n n non contradictory elements. Obviously, there may be many options. In general, you only need to find one.

Simply put: give n n n sets, each set has 2 2 2 elements,
give m m m formulas represent the relationship between the elements of different sets, which requires from n n In n sets, select an element in each set to form a new set, which meets the above requirements m m The situation expressed by m equations.

(it can even be simply understood as having) n n n elements, each element has two values, given m m m restrictions, find legal n n Set of values of n

Of course, there are three situations for a given problem: multiple solutions, unique solutions and no solutions.

2, 2-SAT problem solving:

First, an example is given: a classical 2-SAT problem

have n n n elements, each element can take 0 0 0 or 1 1 1. Give m m m constraints to judge whether there is a solution. If there is a solution, request the solution of any combination method.

(1) How to build a model:

<1> Establishment of points

Obviously, this problem is similar to the difference constraint, and the essence of graph theory is to express the relationship between two points. Therefore, it is easy to think of treating the two values of each element as one point and m m m constraints are regarded as establishing the relationship of edges between different points and establishing a directed graph (generally, there are rings).

Specifically, in the modeling of 2-SAT, the second i i Split i elements into points i i i and points i + n i+n i+n, point i i i stands for the second i i i elements 1 1 one o'clock i + n i+n i+n indicates the second i i i elements 0 0 0.
(there are no special requirements for this, just according to personal habits)

<2> Edge establishment

Every directed edge, from point a a Point a b b b. Indicates that when the element represented by point a selects the value represented by point a, the element represented by point B must select the value represented by point B.
(my expressive ability is limited. I may say something strange.)

Another example would be better understood.

There is one restriction:
For element a and element b, at least one value is 1

Then discuss it by category:
<1> When a = 0 a=0 When a=0, there must be b = 1 b=1 b=1, so the edge is built < a + n , b > <a+n,b> < A + N, b >, i.e a a a take 0 0 At 0, b b b must take 1 1 1.
<2> When a = 1 a=1 When a=1, b b b take 0 0 0 or 1 1 1.
Note: since the edge construction emphasizes the conditions for the establishment of certain conditions, the edge cannot be built for uncertain values, that is, uncertain a = 1 a=1 When a=1 b b b what value is taken, then no edge is built
<3> When b = 0 b=0 When b=0, there must be a = 1 a=1 a=1, so the edge is built < b + n , a > <b+n,a> <b+n,a>
<4> When b = 1 b=1 When b=1, a a The value of a is arbitrary, so no edge is built.

After understanding all the above statements and examples, I believe you have the most basic understanding of the problem scenarios and modeling methods handled by 2-SAT~~

(2) Algorithm for solving 2-SAT problem: Tarjan

Let's review what problems we need to solve:

The problems to be solved are divided into two categories: one is to judge whether there is a solution, and the other is to find any set of solutions (sometimes there are special requirements for the solution, which can be adjusted according to the meaning of the problem).

Then it is obviously solved by using tarjan + shrinkage point.
The correctness is obvious.
Considering the meaning of edges and points, a strong connected component means taking a point in the strong connected component, and all points must be taken.

Therefore, the method of how to judge whether there is a solution is obtained:
For each element i, judge whether point i and point i+n are in the same strongly connected component. If they are, there is no solution. If they are not, there is a solution.

Then think about how to get a feasible solution.
According to Wu Yu - solving 2-sat problem from symmetry, we can get:
If you want to output a feasible solution of the 2-SAT problem, you only need to select and delete it from bottom to top on the DAG obtained after tarjan shrinking point.
That is, it is solved according to the inverse topological order.

Method 1:
The reverse topological order can be obtained from the topology dp on the DAG, and processed in the order of the reverse topological order.

Method 2:
Build DAG's inverse graph, run side topology dp, and the effect is the same as method 1.

Method 3: This is the simplest and most commonly used method.
According to the property that the smaller the number of the connected block, the closer the node is to the leaf node after tarjan shrinks, the node with the smaller number of the connected block is preferred to be selected.

Specific implementation selection method 3, that is, for an element i i i. If point i i If the number of the strongly connected component where i is located is small, then i i i take 1 1 1, otherwise element i i i take 0 0 0.

3, Solve some specific problems: (ybtoj example and Luogu problem)

There are only the following key points to solve the practical problems of 2-SAT:
<1> Consider the practical significance of the value of a variable 0 / 1
<2> Special requirements for solving problems: for example, it is required to maximize the sum of n variables

T1: Logu P4782 [template] 2-SAT problem

A template can be implemented according to the implementation idea above.
I have made mistakes: when building an edge, I built a wrong edge, so I must fix it in advance i i i and points i + n i+n The practical significance of i+n,
After the error, check whether the edge construction is wrong in the first step.

The Code is as follows:

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+60;
int n,m;
int dfn[maxn],low[maxn],tot,col[maxn],ans[maxn];
int s[maxn],top,tim;
int head[maxn],ecnt=-1;
struct mint
{
	int nxt,v;	
}e[maxn<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}	
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,y,a,b;
		scanf("%d%d%d%d",&x,&a,&y,&b);
		if(a==1&&b==1)//b=0 -> a=1 , a=0 ->b=1 
		{
			addline(x+n,y);
			addline(y+n,x);
		}
		if(a==1&&b==0)// a=0 -> b=0 , b=1 -> a=1
		{
			addline(y,x);
			addline(x+n,y+n);	
		}
		if(a==0&&b==1)// a=1 -> b=1 , b=0 -> a=0
		{
			addline(x,y);
			addline(y+n,x+n);		
		}
		if(a==0&&b==0)//a=1 -> b=0 , b=1 -> a=0
		{
			addline(x,y+n);
			addline(y,x+n);
		}
	}
	for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
	for(int i=1;i<=n;++i)
	{
		if(col[i]==col[i+n])
		{
			printf("IMPOSSIBLE\n");
			return 0;	
		}
		ans[i]=col[i]<col[i+n];	
	}
	printf("POSSIBLE\n"); 
	for(int i=1;i<=n;++i) printf("%d ",ans[i]);
	return 0;	
}

T2:HDU 3062 Party & YBTOJ |2-SAT| A. [example 1] Party

I don't have the link QWQ of Hangdian OJ
The questions are as follows

Obviously, this is a 2-SAT template problem. It is required to determine whether there is a solution.
The key is how to build the model.
Note that in this case, although the expression is n elements, each element corresponds to two people, it is essentially n elements rather than 2n elements, that is, two people cannot be regarded as one element respectively, but the common state of two people should be regarded as the meaning of the element.
It can be found that a couple can't appear at the same time, so it's direct 1 1 1 indicates that the husband is present, 0 0 0 means the wife is present.
The final determination of whether there is a feasible solution is to determine whether the two points divided by an element are in the same strongly connected component.

Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+60;
int n,m;
int head[maxn],ecnt=-1;
int dfn[maxn],low[maxn],col[maxn],tot;
int s[maxn],top,tim;
struct mint
{
	int nxt,v;	
}e[maxn<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		scanf("%d",&m);
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col)); 
		ecnt=-1;
		tot=tim=0;
		memset(head,-1,sizeof(head));
		for(int i=1;i<=m;++i)
		{
			int a1,a2,c1,c2;
			scanf("%d%d%d%d",&a1,&a2,&c1,&c2);
			a1=(a1<<1)+c1;
			a2=(a2<<1)+c2;
			addline(a1,a2^1);
			addline(a2,a1^1);
		}
		for(int i=0;i<(n<<1);++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=0;i<n;++i)
		{
			if(col[i<<1]==col[(i<<1)^1])
			{
				flag=1;	
				break;	
			}
		}
		if(flag) printf("NO\n");
		else printf("YES\n");	
	}
	return 0;
}

Here comes another key point: the representation of disassembly point number

It must be remembered that in general, there must be and only two points on the graph corresponding to an element.
The selection of disassembly method must meet the requirements: it is convenient to quickly find its inverse state from a state

There are three common methods of removing points:
<1> Will element i i i disassembly point i i i and points i + n i+n i+n.
<2> Will element i i i split into elements i < < 1 i<<1 I < < 1 and element ( i < < 1 ) + 1 (i<<1)+1 (I < < 1) + 1 (or element) ( i < < 1 ) − 1 (i<<1)-1 (i<<1)−1)
<3> Will element i i i split into elements i < < 1 i<<1 I < < 1 and element ( i < < 1 ) 1 (i<<1)^1 (i<<1)1
Sometimes it can be directly from i i i find its inverse state, but if it is not sure that the input given in the question is i i i or i + n i+n When i+n, we can find its inverse state with the help of a small function.

int get_id(int x)
{
	return x<n ? x+n : x-n;
}

In short, just be flexible.

T3: UVA11294 Wedding & YBTOJ-B. [example 2] wedding

The complete UVA problem of this problem is an extremely chaotic emotional drama
A reminder: there will be a period of maintenance time for UVA every day. If you bind the UVA account but wait for a long time, you might as well pay it another time

How to consider modeling:
For an element i i i. That is, a couple, make 0 0 0 means that the husband sits on the same side as the groom, 1 1 1 means that the wife sits on the same side as the groom.
Run through the 2-SAT template. According to the property of the number order of strongly connected components, that is, the inverse topological order, you can directly go from small to large.

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+30,maxm=1e5+50;
int n,m;
int head[maxn<<2],ecnt=-1;
int dfn[maxn<<2],low[maxn<<2],col[maxn<<2],tot;
int s[maxn<<2],tim,top;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);	
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int get_id(int x)
{
	if(x<=n) return x+n;
	return x-n;
}
int main()
{
	while(1)
	{
		scanf("%d%d",&n,&m);
		if(n==0&&m==0) return 0;
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col));
		tot=tim=0; 
		for(int i=1;i<=m;++i)
		{
			int x,y,c1=0,c2=0;
			char a,b;
			scanf("%d",&x);
			cin>>a;
			scanf("%d",&y);
			cin>>b;//1~n=w , n+1~n*2=h 
			++x;++y;
			if(a=='h') x+=n;
			if(b=='h') y+=n;
			addline(x,get_id(y));
			addline(y,get_id(x)); 
		}
		addline(1,1+n);
		for(int i=1;i<=2*n;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=n;++i)
		{
			if(col[i]==col[i+n])
			{
				flag=1;
				break;
			}
		}
		if(flag)
		{
			printf("bad luck\n");
			continue;
		}
		for(int i=2;i<=n;++i)
		{
			if(col[i]<col[i+n]) printf("%d%c ",i-1,'h');
			else printf("%d%c ",i-1,'w');	
		}
		printf("\n");
	}
	return 0;
}

T4:P5782 [POI2001] Peace Commission & YBTOJ-D. Peace Commission

Let's talk about an interesting little thing. I first went ybtoj on this question, and then went to csdn to search for double experience. I couldn't find any results in the first sentence of the question, and found it in the next few sentences... What is this? Do you have a boss to interpret it.

Continue to look at the questions.
An element represents a party. A party must have and only have one seat in Parliament.
For elements i i i. Consider 0 0 0 means 2 i − 1 2i-1 Representative 2i − 1 in parliament, 1 1 1 indicates 2 i 2i Representative 2i is in Parliament.
Run through the 2-SAT template, and then select from small to large according to the number of strongly connected components.

#include<bits/stdc++.h>
using namespace std;
const int maxn=8e3+30,maxm=2e4+50;
int n,m;
int head[maxn<<1],ecnt=-1;
int dfn[maxn<<1],low[maxn<<1],col[maxn<<1],tot;
int s[maxn<<1],top,tim;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int get_id(int x)
{
	if(x%2==0) return x-1;
	return ++x;	
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		addline(x,get_id(y));
		addline(y,get_id(x));
	}
	for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
	int flag=0;
	for(int i=1;i<=n;++i)
	{
		if(col[(i<<1)]==col[(i<<1)-1])
		{
			flag=1;
			break;
		}
	}
	if(flag) 
	{
		printf("NIE\n");
		return 0;	
	}
	for(int i=1;i<=n;++i)
	{
		if(col[(i<<1)]<col[(i<<1)-1]) printf("%d\n",i<<1);
		else printf("%d\n",(i<<1)-1); 
	}
	return 0;
}

My 2-SAT template runs fairly fast, basically about 2 ~ 3 pages z before the optimal solution.

T5:P4171 [JSOI2010] man Han banquet & YBTOJ-F. man Han banquet

It's disgusting that this topic description is true. The translation of adult words is:
give n n n elements, each element has 0 / 1 0/1 Two values of 0 / 1 are given m m m constraints to judge whether there is a feasible solution.
Water, it's too water.
Consider modeling,
For elements i i i， 0 0 0 means full method, 1 1 1 means Chinese practice. Run through the template to judge whether there is a solution.
Water, very water.
However, because the problem is too chaotic, it is easy to make mistakes while building..
Pay attention to this.
Finally, I think oi is an algorithm competition, not a reading comprehension competition.....
Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=105,maxm=1005;
int n,m,k;
int head[maxn<<1],ecnt=-1;
int dfn[maxn<<1],low[maxn<<1],col[maxn<<1],tot;
int s[maxn<<1],tim,top;
struct mint
{
	int nxt,v;	
}e[maxm<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	scanf("%d",&k);
	for(int q=1;q<=k;++q)
	{
		scanf("%d%d",&n,&m);	
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(col,0,sizeof(col));
		memset(low,0,sizeof(low));
		tot=tim=0;
		memset(s,0,sizeof(s));
		top=0;
		int cnt=0;
		for(int i=1;i<=m;++i)
		{
			char a,b;
			int x,y;
			cin>>a;
			scanf("%d",&x);
			cin>>b;
			scanf("%d",&y);
			if(a=='m'&&b=='m')//b=1->a=0 , a=1-->b=0
			{
				addline(y,x+n);
				addline(x,y+n);	
			}
			if(a=='m'&&b=='h')//b=0->a=0 , a=1->b=1
			{
				addline(y+n,x+n);
				addline(x,y);
			}
			if(a=='h'&&b=='m')//b=1->a=1 , a=0->b=0
			{
				addline(x+n,y+n);
				addline(y,x);
			}
			if(a=='h'&&b=='h')//b=0->a=1 , a=0->b=1
			{
				addline(y+n,x);
				addline(x+n,y);
			}
		}
		for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=n;++i)
		{
			if(col[i]==col[i+n])
			{
				flag=1;
				break;
			}
		}
		if(flag) printf("BAD\n");
		else printf("GOOD\n"); 
	}
	return 0;	
}

T6:P3209 [HNOI2010] plan determination & E. Plan

This is the most difficult and best of the six questions mentioned so far. Unfortunately, the difficulty is not in 2-SAT....
The plane graph is mentioned in the question, so we must think of the relevant theorems and properties of the plane graph.

A plane graph is one that can be drawn on a two-dimensional plane so that any two edges do not intersect at positions other than vertices.

First, the questions given in the title m < = 100000 m<=100000 M < = 100000 is actually a false data range, because according to the nature of the plan,
A plan must meet m < = 3 ∗ n − 6 m<=3*n-6 M < = 3 * n − 6, so actually m m The maximum value of m is also 600 600 About 600.
I will blog about the floor plan later, but if you want to know now, please go to Plan part of OIWIKI.
Skip here.

Hamiltonian path is a ring.
It is easy to find that an edge that is not on the Hamiltonian path can be drawn inside and outside the Hamiltonian path.
At the same time, if the two paths intersect when they are inside the Hamiltonian path, they must also intersect when they are outside at the same time.

Considering how to model, each edge not on the Hamiltonian path is divided into two points to represent that the edge is drawn inside and outside the ring respectively.
For the edges on any two non Hamiltonian paths, judge whether they intersect when they are in the ring at the same time,
And establish restrictions.

After all the drawings are built, just run through the template.
It should not be a problem to judge whether there is a solution.

#include<bits/stdc++.h>
using namespace std;
const int maxn=250,maxm=1e6+50;
int n,m;
int head[maxm],ecnt=-1;
int dfn[maxm],low[maxm],col[maxm],tot;
int s[maxm],top,tim;
int id[maxm],pla[maxm];
int x[maxm],y[maxm];
bool G[maxn][maxn];
int cnt;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
struct edge
{
	int u,v;
}E[maxm];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);	
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	int t;
	scanf("%d",&t);
	for(int q=1;q<=t;++q)
	{
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col));
		memset(pla,0,sizeof(pla)); 
		memset(G,0,sizeof(G));
		cnt=tim=tot=0;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;++i)
		{
			scanf("%d%d",&x[i],&y[i]);	
		}
		for(int i=1;i<=n;++i)
		{
			scanf("%d",&id[i]);
			pla[id[i]]=i;
			G[id[i]][id[i-1]]=G[id[i-1]][id[i]]=1;	
		}
		G[id[1]][id[n]]=G[id[n]][id[1]]=1;
		if(m>3*n-6) 
		{
			printf("NO\n");
			continue;	
		}
		for(int i=1;i<m;++i)
		{
			int a=x[i],b=y[i];
			if(G[a][b]) continue;
			for(int j=i+1;j<=m;++j)
			{
				int c=x[j],d=y[j];
				if(pla[a]>pla[b]) swap(a,b);
				if(pla[c]>pla[d]) swap(c,d);
				if((pla[a]<pla[c] && pla[c]<pla[b] && pla[b]<pla[d]) || (pla[c]<pla[a] && pla[a]<pla[d] && pla[d]<pla[b]))
				{
					addline(i,j+m);
					addline(j,i+m);
					addline(i+m,j);
					addline(j+m,i);
				}
			}
		}
		for(int i=1;i<=m*2;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=m;++i)
		{
			if(col[i]==col[i+m]) 
			{
				flag=1;
				break;
			}
		}
		if(flag) printf("NO\n");
		else printf("YES\n");
	}
	return 0;
}	

How to judge the intersection of two edges in the ring is a very important small detail:
It is easy to find that when one edge intersects with another, there must be a case where one vertex of each edge is located between two points of the other edge.
Play with your hands and draw more situations. You can find that this conclusion is tenable.

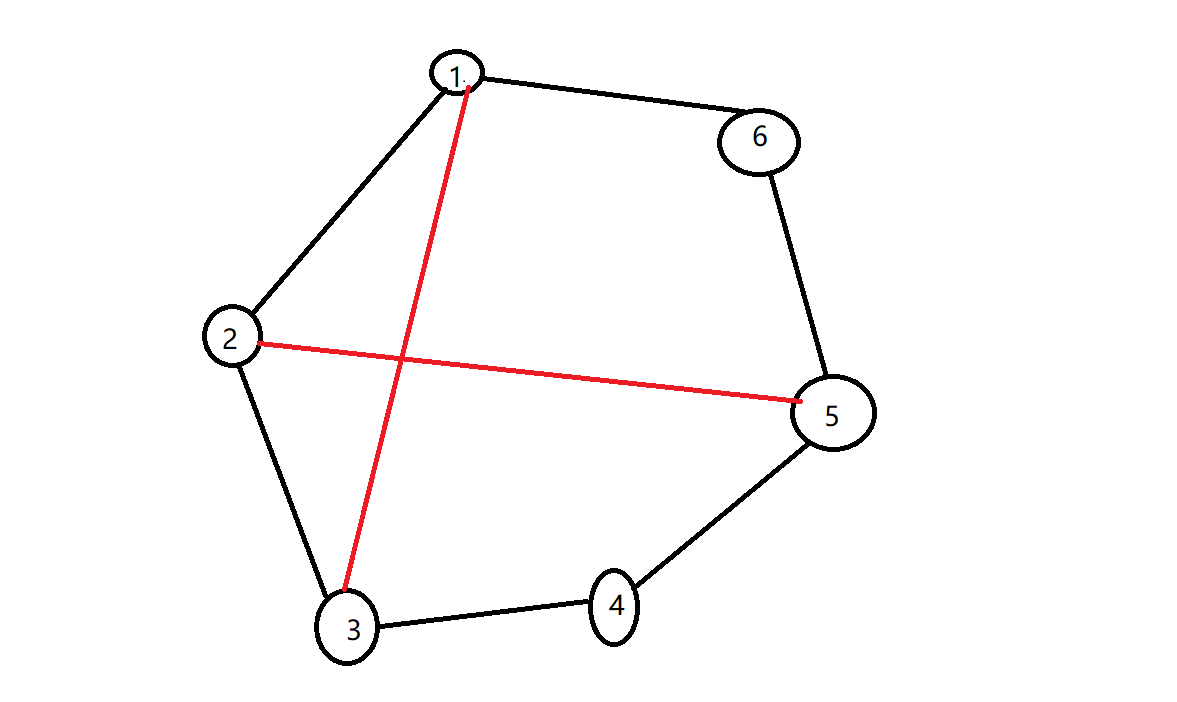
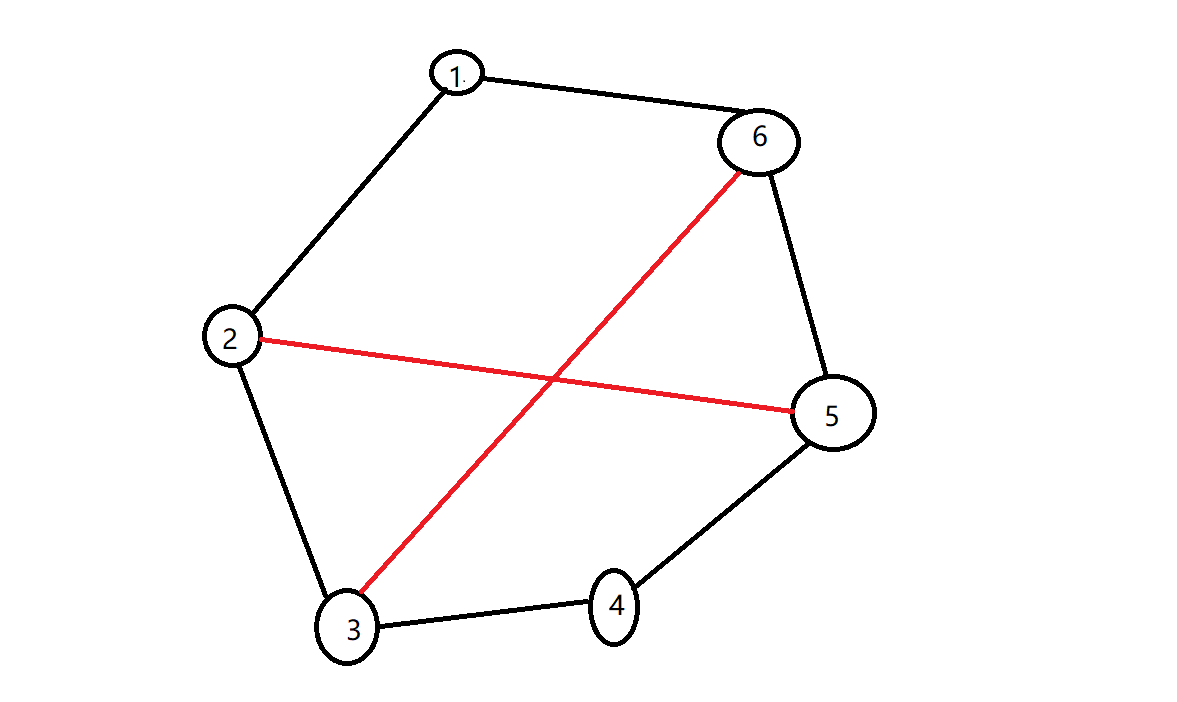
Intuitively, you may think that there will be problems when an edge crosses n to 1, but in fact, any edge can be regarded as not crossing n to 1.
Therefore, this conclusion will not be wrong because of whether it crosses a certain position of the ring

4, Postscript:

The significance of this blog is to facilitate you to find all kinds of double experience and summarize various solutions, errors and some small details of the 2-SAT problem.
In fact, this blog is only part of the solution of 2-SAT. many key contents, such as finding special sets, have not been included.
Therefore, there will be the next article as a supplement! yeah

Some nonsense:
So in fact, the code of 2-SAT is relatively simple and the model is relatively general. It seems that there won't be a lot of questions to be tested..
Otherwise, some questions can't be seen as 2-SAT in the exam, or 2-SAT like BJOI perfect tower defense is just a big simulation of secondary content..