A. Gratitude
Main idea of the title:
Count the occurrence times of different strings, and output them according to the occurrence times of strings from more to less. If the occurrence times are the same, the string at the back of the occurrence position will be output.
Simple string statistics, pay attention to the output when the number of times is the same.
#include<bits/stdc++.h>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
const ll mod=1000000007;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
inline ll lowbit(ll x){return x&(-x);}
struct node{
string s;
int id;
int num;
}p[maxn];
bool cmp(node a,node b){
if(a.num!=b.num) return a.num>b.num;
return a.id>b.id;
}
map<string,int>mp;
int main(){
int n,k;
cin>>n>>k;
int cnt=1;
getchar();//Absorb blank lines
for(int i=0;i<3*n;i++){
string s;
getline(cin,s);
if(mp[s]==0) mp[s]=cnt++;
int id=mp[s];
p[id].num++;
p[id].id=i;//Error prone point
p[id].s=s;
}
sort(p+1,p+cnt+1,cmp);
for(int i=1;i<=min(k,cnt-1);i++){//Note the number of output answers
cout<<p[i].s<<endl;
}
}
C. Safe Distance
Main idea of the title:
Find the maximum value of the minimum distance from other n people in an area with length X and width Y from (0,0) to (X,Y).
To solve the maximum value of the minimum value and the minimum value of the maximum value, the dichotomy is generally used to search the answer.
So how does this question judge the "answer"?
Consider that there is a circle with the same radius from (0,0) to (X,Y). If the circle can pass smoothly, that is, there will be no circle boundary connecting the upper and lower boundaries, left and right boundaries, upper and right boundaries, lower and left boundaries of the area, it shows that the "answer" is feasible. Enlarge the range and continue to search for the answer; Otherwise, it means that the "answer" is too large and needs to be narrowed down.
At the same time, the connectivity is maintained with the help of union query set.
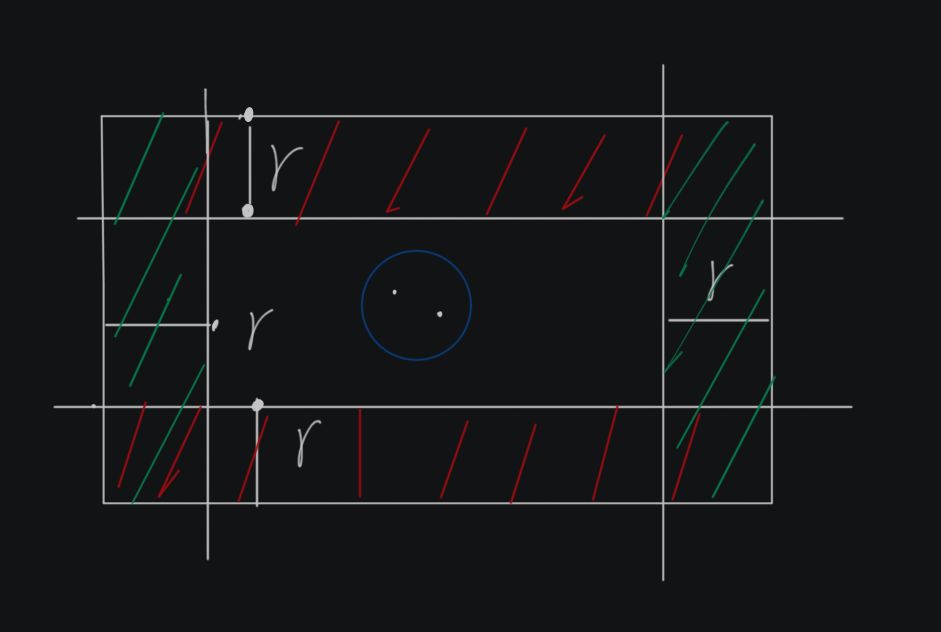
If the distance between two points is less than radius r, they are connected.
Examples of feasible situations:

Examples of infeasibility:

#include<bits/stdc++.h>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=1e4+10;
const ll mod=1000000007;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
inline ll lowbit(ll x){return x&(-x);}
int n,m,k;
int fa[maxn];
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
struct dots{
double x,y;
}a[maxn];
bool check(double r){
for(int i=1;i<=k+4;i++) fa[i]=i;
for(int i=1;i<=k;i++){
if(m-a[i].y<r){//If the distance from the point to the upper boundary is less than the radius, the point is connected to the upper boundary
int u=find(i);
int v=find(k+1);
if(u!=v) fa[u]=v;
}
if(a[i].y<r){//If the distance between the point and the lower boundary is less than the radius, the point is connected to the lower boundary
int u=find(i);
int v=find(k+2);
if(u!=v) fa[u]=v;
}
if(a[i].x<r){//If the distance between the point and the left boundary is less than the radius, the point is connected to the left boundary
int u=find(i);
int v=find(k+3);
if(u!=v) fa[u]=v;
}
if(a[i].x>n-r){//If the distance between the point and the right boundary is less than the radius, the point is connected to the right boundary
int u=find(i);
int v=find(k+4);
if(u!=v) fa[u]=v;
}
for(int j=1;j<i;j++){
double dis=(a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y);
if(dis<4*r*r){//If the distance between two points is less than the diameter, the two points are connected
int u=find(i);
int v=find(j);
if(u!=v) fa[u]=v;
}
}
}
if(find(k+1)==find(k+2)||find(k+3)==find(k+4)||find(k+1)==find(k+4)||find(k+3)==find(k+2)) return 0;
return 1;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;i++){
scanf("%lf%lf",&a[i].x,&a[i].y);
}
double l=0,r=max(n,m);
while(r-l>=1e-6){//Dichotomy search answer
double mid=(l+r)/2.0;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.6lf\n",l);
return 0;
}
D. Jogging
Main idea of the title:
Jog on the street and ask how many different routes you can run at most if you meet the upper and lower limits of running distance.
Each time you run on an edge you haven't run before, you can be regarded as running a different route.
So it depends on the number of sides that can be reached at most,
An edge has two endpoints. If the minimum value of the shortest distance to reach the two endpoints is less than the upper limit of the running distance, it means that the edge can be reached, and the number is increased by one.
#include<bits/stdc++.h>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
const ll mod=1000000007;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
inline ll lowbit(ll x){return x&(-x);}
vector<P>v;//Record the two endpoints of the edge
int cnt,e[maxn],w[maxn],ne[maxn],h[maxn];//Chained forward star map
void add(int x,int y,int z){
e[cnt]=y;
w[cnt]=z;
ne[cnt]=h[x];
h[x]=cnt++;
}
int dis[maxn],vis[maxn];
void dij(){//dij algorithm solves the shortest distance from the starting point 0 to each endpoint
memset(dis,0x3f,sizeof(dis));
priority_queue<P,vector<P>,greater<P> >q;
q.push(make_pair(0,0));
dis[0]=0;
while(!q.empty()){
int p=q.top().second;
q.pop();
if(vis[p]) continue;
vis[p]=1;
for(int i=h[p];i!=-1;i=ne[i]){
int tmp=e[i];
if(dis[tmp]>dis[p]+w[i]){
dis[tmp]=dis[p]+w[i];
q.push(make_pair(dis[tmp],tmp));
}
}
}
}
int main(){
memset(h,-1,sizeof(h));
int n,m,l,r;
scanf("%d%d%d%d",&n,&m,&l,&r);
while(m--){
int x,y,w;
scanf("%d%d%d",&x,&y,&w);
v.push_back(make_pair(x,y));
add(x,y,w);
add(y,x,w);
}
dij();
int ans=0;
for(int i=0;i<v.size();i++){
if(2*min(dis[v[i].fi],dis[v[i].se])<r) ans++;
}
printf("%d\n",ans);
return 0;
}
E. Cakes
Title Link
Water question~
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e4+4;
int main(){
int n;
cin>>n;
int ans=1000000;
int a,b,c;
for(int i=0;i<n;i++){
cin>>a>>b;
c=b/a;
ans=min(ans,c);
}
cout<<ans<<endl;
return 0;
}
K. Unique Activities
Main idea of the title:
Look for the substring whose value appears once and appears at the top.
Binary string length, enumerate the substrings of this length, and count their occurrence times.
However, if the substring is retrieved directly and violently, the memory is out of limit.
The correct solution of this problem requires string hash (new knowledge get √)
#include<bits/stdc++.h>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=3e5+10;
const ll mod=1000000007;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
typedef unsigned long long ull;
inline ll lowbit(ll x){return x&(-x);}
const int seed=13331;
ull p[maxn];
ull ha[maxn];
unordered_map<ull,int>mp;
string s;
void init(){
p[0]=1;
for(int i=1;i<=maxn;i++) p[i]=p[i-1]*seed;
}
bool check(int len){
int num=0;
mp.clear();
for(int i=1;i<s.size();i++){
int y=i+len-1;
if(y>=s.size()) break;
int x=i;
ull tmp=ha[y]-ha[x-1]*p[len];//Gets the hash value of the string
mp[tmp]++;
if(mp[tmp]==1) num++;
if(mp[tmp]==2) num--;
}
return num;
}
int main(){
init();
cin>>s;
s="."+s;
for(int i=1;i<s.size();i++){//String hash
ha[i]=ha[i-1]*seed+s[i]-'A'+1;
}
int l=1,r=s.size()-1;
while(l<r){
int mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid+1;
}
mp.clear();
for(int i=1;i<s.size();i++){
int y=i+l-1;
if(y>=s.size()) break;
int x=i;
ull tmp=ha[y]-ha[x-1]*p[y-x+1];
mp[tmp]++;
}
for(int i=1;i<s.size();i++){
int y=i+l-1;
if(y>=s.size()) break;
int x=i;
ull tmp=ha[y]-ha[x-1]*p[y-x+1];
if(mp[tmp]==1){
cout<<s.substr(x,l)<<endl;
break;
}
}
return 0;
}