#1 function recursion

Function recursion refers to the function calling its own technology. Function recursion is very elegant in the way of thinking, which reflects the idea of transforming large-scale problems into similar problems of lower scale; But in terms of algorithm efficiency, recursion is a low efficiency algorithm.

Recursive algorithm must meet two conditions: 1 There is an exit (the solution to a minimum scale problem); 2. The method of transforming a large-scale problem into a similar problem of a lower scale. The expression of sequence is: 1. Know the initial items (a0,a1,a2, etc.); 2. Know the recurrence formula (an+1=f(an)). This ensures that the recursion will not proceed indefinitely, and also reflects the function structure of the recursive algorithm and the thinking mode of the recursive algorithm (reducing the problem scale & providing the solution to the lowest scale problem).

#2 several simple examples of function recursion

//Print each bit of the given number num from high to low
void print(int num) {
	if (num <= 9 and num >= 0)//So the starting term a0 is the exit of recursion
		printf("%d	",num);
	else {
		print(num / 10);
		printf("%d	", num % 10);//Equivalent to the general term formula an=f(an-1)
	}

	return;
}
//Print 1234
//=Print 123 + Print 4
//=Print 12 + Print 3 + Print 4
//=Print1 + print2 + print3 + print4
//Print 1 is the lowest scale problem (print one digit), and both sides of the equal sign reflect the reduction of the problem scale

//Calculates the length of a given string without using temporary variables
int my_strlen(char* str) {
	if (*str == '\0')
		return 0;        //Initial term, minimum scale problem
	else {
		return my_strlen(str+1)+1;//Recurrence formula
	}
}
//Calculate the length of "China" (pointer refers to C)
//=Calculate the length of C hina (the pointer moves to the right to refer to h) + 1
//=Calculate the length of ina (the pointer moves right to point to i) + 1 + 1
//...
//=Calculate the length of '\ 0' (pointer refers to '\ 0') + 1 + 1 + 1 + 1
//Calculate the length of '\ 0' as the minimum size problem

//Calculate the nth term of Fibonacci sequence 1 1 2 3 5 8 13
int sequence(int n) {

	if (n == 1 or n == 2) return 1;
	else
		return sequence(n - 1) + sequence(n - 2);
}

//The initial term and recurrence formula of the sequence are very obvious

#From the calculation of Fibonacci sequence to see the operation efficiency of recursive algorithm

Calculating a(50) requires calculating a(49) and a(48), while calculating a(49) requires calculating a(48) and a(47). a(48) was repeated. Similarly, when calculating a(48), a(47) is repeatedly calculated. As shown in the figure:

a(50)
a(49)+a(48)
a(48)+a(47)+a(47)+a(46)
a(47)+a(46)+a(46)+a(45)+a(46)+a(45)+a(45)+a(44)
...
It seems that the first few items will be calculated many times.
We might as well calculate the following calculation a(40)Time a(3)The number of times to be calculated, which is due to calculation a(50)It often takes 10 years min About, while calculating a(40)Maybe only 10 s about. We can also see the difference of time complexity of recursive algorithm. Not to mention its space complexity (a common problem in recursive algorithms is stack overflow).

int count3_40 = 0;//The number of times sequence(3) is calculated when sequence(40) is calculated using the recursive algorithm of Fibonacci sequence
int count30_40 = 0;//The number of times sequence(30) is calculated when sequence(40) is calculated using the recursive algorithm of Fibonacci sequence
int sequence(int n) {
	if (n == 3) ++ count3_40;
	if (n == 30) ++count30_40;
	if (n == 1 or n == 2) return 1;
	else
		return sequence(n - 1) + sequence(n - 2);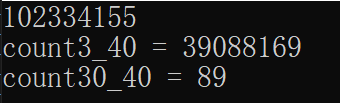

It can be found that a(3) has been repeatedly calculated more than 30 million times. It can be seen that the recursive algorithm has high redundancy.

#4 iteration and recursion

The recursive algorithm for calculating Fibonacci sequence is changed to iteration, that is, loop.

int sequence_loop(int n) {
	int a = 1;    //i
	int b = 1;	  //i+1
	int c = 0;	  //i+2
	if (n <= 2) return 1;
	for (int i = 3; i <= n;++i) {
		c = a + b;
		a = b;
		b = c;
		

	}
	return c;
	
}
//First consider the actual application scenario, and then consider how to implement it. Called TDD, test driven development.
//Recursion contains a large number of repeated operations, and the operation efficiency is very low. It should be replaced by iteration (loop).

Recursive algorithm is elegant in thinking mode, but it is not satisfactory in efficiency. If you want the simplicity of recursive algorithm and the efficiency of iterative algorithm, you should find a general method to change recursive algorithm into iterative algorithm. I have encountered this method when learning data structures.