As the first simulation competition after the beginning of high school, its significance is naturally unique.

There are three questions, which are all simple in person. (but time is too short. Can you give more examples by way of Tucao? Make complaints about hand disability.)

T1: given a polynomial (ax + by)k, request the coefficients of xn ym term after polynomial expansion.

Obviously, it has something to do with Yang Hui's triangle, but I think the latter two questions are recursive, and the formula is very easy to deduce. I just did the last question, and then forgot to take the mold (SAD)

First, we need to build Yanghui triangle

for(int i=1 ; i<=k+1 ; i++){
	f[i][1] = 1;
	f[i][i] = 1;  //Preprocess the 1 of the first column and the rightmost column first
}
for(int i=3 ; i<=k+1 ; i++){ //2 has been pretreated, starting from 3
	for(int j=2 ; j<i ; j++){ //Note to start with 2
		f[i][j] = (f[i-1][j-1]+f[i-1][j])%mod; //Pay attention to mold taking
	}
}

However, we find that there are not only x and y, but also coefficients... Which can only pass 50% of the test points.

The coefficient needs to be pushed with paper. You can expand each item, take ax and by as a whole, and you will find that the final answer needs to be multiplied by n times a and m times b.

Just multiply it at the end. Don't forget to take the mold!

Final code:

#include<bits/stdc++.h>
using namespace std;
const int mod = 10007;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48 ; ch=getchar();}
	return x*f;
}
int a,b,k,n,m;
int f[1100][1100];
int ans;
int main(){
	freopen("factor.in","r",stdin);
	freopen("factor.out","w",stdout);
	a=read();b=read();k=read();n=read();m=read();
	if(k==0){
		printf("1\n");
		return 0;
	}
	for(int i=1 ; i<=k+1 ; i++){
		f[i][1] = 1;
		f[i][i] = 1;
	}
	for(int i=3 ; i<=k+1 ; i++){
		for(int j=2 ; j<i ; j++){
			f[i][j] = (f[i-1][j-1]+f[i-1][j])%mod;
		}
	}
	ans = f[k+1][k-n+1];
	for(int i=1 ; i<=n ; i++) ans = (ans%mod) * (a%mod) % mod;
	for(int i=1 ; i<=m ; i++) ans = (ans%mod) * (b%mod) % mod;
	printf("%d",ans%mod);
	return 0;
}

T2: the tower of Hanoi is composed of disks of different sizes numbered from 1 to N and three columns a, B and c. at the beginning, these n disks are sleeved on column a from large to small, as shown in the figure. It is required to move the N disks on column a to column c according to the following rules:

For a classic recursive problem, considering an N, it is easy to find that it can be derived from n-1. Moreover, due to the addition of a disc, the number of times to move needs to be multiplied by two. Finally, don't forget to add 1, which is the last step to move to the column.

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48 ; ch=getchar();}
	return x*f;
}
long long f[100];
int main(){
	freopen("hanoi.in","r",stdin);
	freopen("hanoi.out","w",stdout);
	int n;
	n=read();
	f[1] = 1;
	f[2] = 3;
	for(int i=3 ; i<=30 ; i++) f[i] = 2*f[i-1] + 1; //Be careful not to be crippled. Write i as n in the exam and hang up / (ㄒ o ㄒ)/~~
	printf("%lld\n",f[n]);
	return 0;
}

 T3: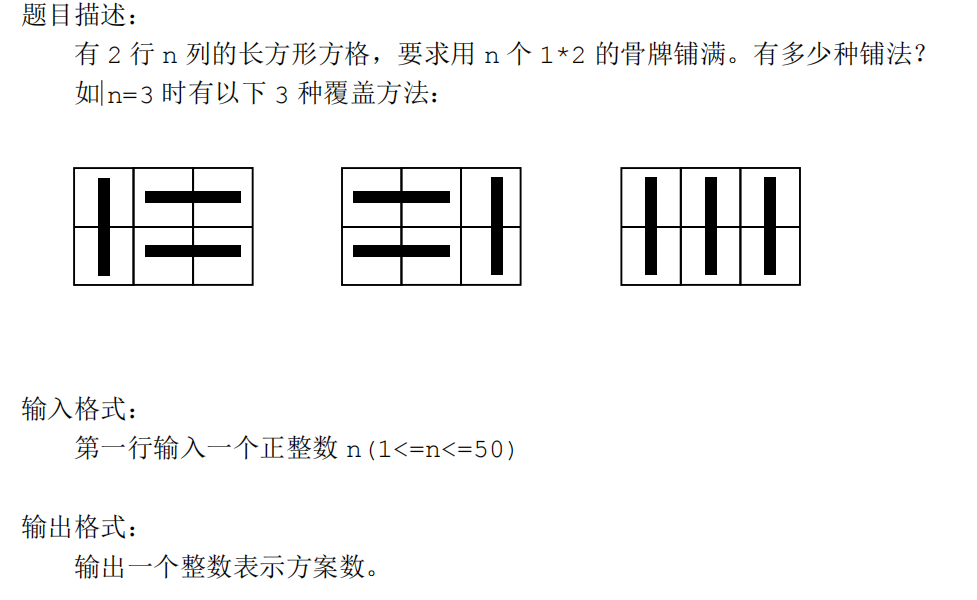

It's also a recursive question. This position can be deduced from the first two positions (it's easy to think of it).

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48 ; ch=getchar();}
	return x*f;
}
long long f[100];
int main(){
	freopen("domino.in","r",stdin);
	freopen("domino.out","w",stdout);
	int n;
	n=read();
	f[1] = 1;
	f[2] = 2;
	for(int i=3 ; i<=50 ; i++) f[i] = f[i-1]+f[i-2];
	printf("%lld\n",f[n]);
	return 0;
}

This simulation competition should be regarded as an accumulation of experience. In the future, we should pay more attention to details and don't be disabled!!!