Note:
Title:
Give you a linked list with a length of n. each node contains an additional random pointer random, which can point to any node or empty node in the linked list.
Construct a deep copy of this linked list. The deep copy should consist of exactly n new nodes, in which the value of each new node is set to the value of its corresponding original node. The next pointer and random pointer of the new node should also point to the new node in the replication linked list, and these pointers in the original linked list and the replication linked list can represent the same linked list state. The pointer in the copy linked list should not point to the node in the original linked list.
For example, if there are two nodes X and Y in the original linked list, where x.random -- > y. Then, the corresponding two nodes X and Y in the copy linked list also have x.random -- > y.
Returns the header node of the copy linked list.
A linked list composed of n nodes is used to represent the linked list in input / output. Each node is represented by a [val, random_index]:
Val: one represents node Integer of val.
random_index: the node index pointed to by the random pointer (ranging from 0 to n-1); null if it does not point to any node.
Your code only accepts the head node of the original linked list as the incoming parameter.
Example 1:
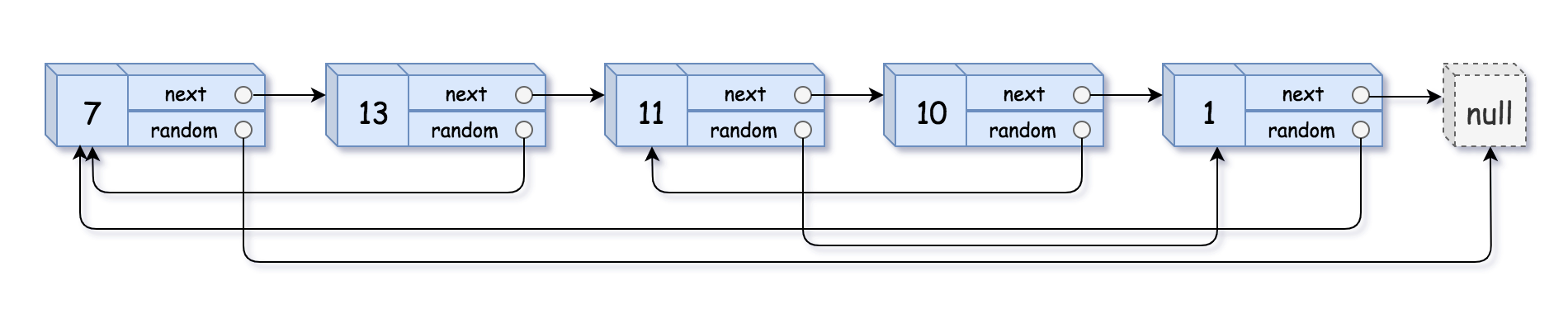
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]
Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1], [2,1]]
Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]
Tips:
0 <= n <= 1000
-10000 <= Node.val <= 10000
Node.random is empty (null) or points to a node in the linked list.
Solution:
Method 1 hash table
Using the query characteristics of the hash table, consider building the key value pair mapping relationship between the original node and the new node, and then traverse the next and random reference points of each node of the new linked list.
initialization
Initialize the new node saved in the hash table nodes. Note that the title requires that the new linked list cannot point to the node of the original linked list, so it is necessary to construct a new node with new.
Copy linked list
Make the node point to the head of the original node;
Adjust the next and random pointers of the new node map[node] corresponding to the node;
Node traverses to the next node of node;
Return value
The head node map[head] of the new linked list;
Complexity analysis
Time complexity O(N): traverse the linked list in two rounds, using O(N) time.
Spatial complexity O(N): the hash table dic uses additional space of linear size.
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
Node* copyRandomList(Node* head) {
map<Node*,Node*> nodes;
Node* node=head;
//Construct a map of [original node, new node]
//Note that the problem requires that the new linked list cannot point to the node of the original linked list, so you need to use new to construct a new node
while(node!=NULL){
nodes[node]=new Node(node->val);
node=node->next;
}
node=head;
//Adjust the next and random pointers of the new node
while(node!=NULL){
nodes[node]->next=nodes[node->next];
nodes[node]->random=nodes[node->random];
node=node->next;
}
return nodes[head];
}
};
Method 2: splicing + splitting
Consider building a spliced linked list of original node 1 - > new node 1 - > original node 2 - > new node 2 - >... So that you can find the new random pointing node corresponding to the new node while accessing the random pointing node of the original node.
Algorithm flow:
-
Construct a new node and adjust the next pointer of the new node: set the original linked list as node1 → node2 →... And the constructed splicing linked list is as follows:
node1→node1new →node2→node2new→⋯ -
The random direction of each node in the new linked list: when accessing the original node, the random point to the node Random corresponds to the new node node The random pointing node of next is node random. next .
-
Split the original / new linked list: set node / node2 to point to the original / new chain header node respectively, and traverse the node next = node. next. Next and node2 next = node2. next. Next separate the two linked lists.
-
Return the header node head2 of the new linked list.
Complexity analysis
Time complexity O(N): three rounds of traversal of the linked list, using O(N) time.
Space complexity O(1): node reference variables use additional space of constant size.
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
Node* copyRandomList(Node* head) {
Node* node=head;
if(head==NULL){
return NULL;
}
//Construct a new node and adjust the next pointer of the new node
while(node!=NULL){
Node* temp=new Node(node->val);
temp->next=node->next;
node->next=temp;
node=temp->next;
}
//Adjust the rondom pointer of the new node
node=head;
while(node!=NULL){
if(node->random!=NULL){
node->next->random=node->random->next;
}
else{
node->next->random=NULL;
}
node=node->next->next;
}
node=head;
Node* head2=head->next;
Node* node2=head2;
//Split linked list
while(node2->next!=NULL){
node->next=node2->next;
node=node->next;
node2->next=node->next;
node2=node2->next;
}
//Add null at the end of the original linked list
node->next=NULL;
return head2;
}
};