A,Alice and Bob
General idea of the topic
There are two piles of stones. The number of stones is n n n and m m m. Order of magnitude in 5 ∗ 1 0 3 5*10^3 5 * 103, now everyone takes turns to choose and must choose a pile to take away k > 0 k>0 k> 0 stones and take them from another pile s ∗ k s*k s * k stones s ≥ 0 s\ge0 s ≥ 0, that is, the second selection can be taken away 0 0 0 stones. A l i c e Alice Alice took the lead, B o b Bob Bob's backhand, the first person who can't operate, loses. Ask who won the game.
Solution
Test site: Game
First, let's consider using f [ i ] [ j ] f[i][j] f[i][j] stands for the first pile of i i i , stones, the second pile has j j The first hand of a stone will win ( t r u e ) (true) (true) or must fail ( f a l s e ) (false) (false).
initialization f [ 0 ] [ 0 ] = f a l s e , f [ 1... n ] [ 0 ] = f [ 0 ] [ 1... n ] = t r u e f[0][0] = false,f[1...n][0]=f[0][1...n]=true f[0][0]=false,f[1...n][0]=f[0][1...n]=true.
Next, violently enumerate the first pile of stones and the second pile of stones. If a certain point is in the state of failure now, it means that adding several qualified left and right stones must be in the state of victory.
But at this point of view, the complexity is different O ( n 3 log n ) O(n^3\log n) O(n3logn), let's take a closer look and assume that for two situations ( i , p ) , ( i , q ) (i,p),(i,q) (i,p),(i,q) are inevitable States, and it is assumed that p > q p>q p> Q, then we can ( i , p ) (i,p) (i,p) when the situation ( 0 , p − q ) (0,p-q) (0,p − q) stones to turn the situation into ( i , q ) (i,q) (i,q) at this time, it becomes a winning state again, which is contradictory, indicating that there is a conflict for the first pile i i i stone, the second pile of stones only one case is bound to fail. So we have the complexity O ( n 2 log n ) O(n^2\log n) O(n2logn).
However, this problem is still very metaphysical. The approximate complexity of the official explanation is O ( n ) O(n) O(n) b i t s e t bitset bitset substitution b o o l bool bool array time can come 300 m s 300ms About 300ms.
#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define all(__vv__) (__vv__).begin(), (__vv__).end()
#define endl "\n"
#define pai pair<int, int>
#define ms(__x__,__val__) memset(__x__, __val__, sizeof(__x__))
#define rep(i, sta, en) for(int i=sta; i<=en; ++i)
#define repp(i, sta, en) for(int i=sta; i>=en; --i)
#define debug(x) cout << #x << ":" << x << '\n'
typedef tuple<int, int> tup;
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll read() { ll s = 0, w = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1; for (; isdigit(ch); ch = getchar()) s = (s << 1) + (s << 3) + (ch ^ 48); return s * w; }
inline void print(ll x, int op = 10) { if (!x) { putchar('0'); if (op) putchar(op); return; } char F[40]; ll tmp = x > 0 ? x : -x; if (x < 0)putchar('-'); int cnt = 0; while (tmp > 0) { F[cnt++] = tmp % 10 + '0'; tmp /= 10; } while (cnt > 0)putchar(F[--cnt]); if (op) putchar(op); }
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1) ans *= a; b >>= 1; a *= a; } return ans; } ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
const int dir[][2] = { {0,1},{1,0},{0,-1},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1} };
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF64 = 0x3f3f3f3f3f3f3f3f;
const int N = 5e3 + 1;
struct Node {
ll val;
int id;
bool operator < (const Node& opt) const {
return val < opt.val;
}
};
ll n, m;
bitset<N> f[N];
void init() {
f[0][0] = 0;
rep(i, 1, N - 1)
f[i][0] = f[0][i] = 1;
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
if (!f[i][j]) {
for (int a = 1; i + a < N; ++a) {
for (int b = 0; b + j < N; b += a) {
f[i + a][j + b] = 1;
}
}
for (int a = 1; j + a < N; ++a) {
for (int b = 0; b + i < N; b += a) {
f[i + b][j + a] = 1;
}
}
break;
}
}
}
}
int solve() {
n = read(), m = read();
return f[n][m];
}
int main() {
init();
int T = read(); rep(_, 1, T)
{
//solve();
cout << (solve() ? "Alice" : "Bob") << endl;
}
return 0;
}
B,Ball Dropping
General idea of the topic
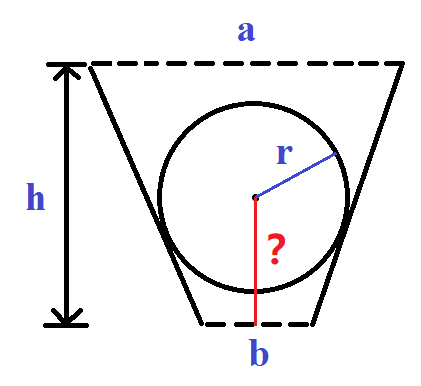
The following image shows a , b , h , r a,b,h,r a. B, h, R, you should judge whether the ball will pass through the funnel. If not, the height from the center of the output circle to the bottom of the loophole.
Solution
Test site: computational geometry
- First consider when it will pass through the funnel if and only if 2 ∗ r ≥ b 2*r\ge b 2 * when r ≥ b.
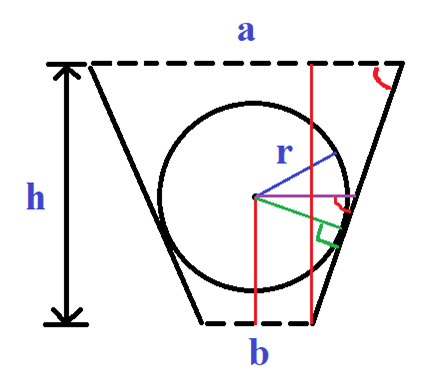
- At other times, calculate the angle of the upper right corner of the funnel θ \theta θ, Borrowing radius r r r and b 2 \displaystyle\frac{b}{2} 2b , you can calculate the bottom of the small triangle, and then tan \tan tan is OK. Borrow the picture of the official caption.
int solve() {
double r, a, b, h;
cin >> r >> a >> b >> h;
if (r * 2 <= b) {
cout << "Drop" << endl;
}
else {
double sita = atan(h / ((a - b) / 2));
double L = r / sin(sita) - b / 2;
double res = L * tan(sita);
cout << "Stuck" << endl;
printf("%.6f\n", res);
}
return 1;
}
C,Determine the Photo Position
General idea of the topic
Give a n ∗ n n*n N * n 01 01 01 matrix, you want to use 1 ∗ m 1*m Matrix filling of 1 * m 0 0 0, ask how many filling schemes you have.
1 ≤ n , m ≤ 2000 1\le n,m\le 2000 1≤n,m≤2000
Solution
Check in question, continuous simulation 0 0 0.
char s[N], t[N];
int solve() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
vector<string> a(n);
for (int i = 0; i < n; ++i)
cin >> a[i];
string b;
cin >> b;
int res = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
int cnt = 0;
int k = j;
while (k < n && a[i][k] == '0') ++k;
res += max(0ll, k - j - m + 1);
j = k;
}
}
print(res);
return 1;
}
F,Find 3-friendly Integers
General idea of the topic
Define a number as 3 − f r i e n d l y 3-friendly 3 − friendly, if and only if a substring of this number x m o d 3 ≡ 0 x\mod 3\equiv 0 xmod3≡0. seek [ l , r ] [l,r] Yes in [l,r] 3 − f r i e n d l y 3-friendly 3 − number of friendly.
Solution
Test site: Digital dp thinking
First, we know that a number is 3 3 A multiple of 3, which can add and sum several items m o d 3 \mod 3 mod3, and then we know ( a + b + c ) m o d 3 ≡ a m o d 3 + b m o d 3 + c m o d 3 (a+b+c)\mod 3\equiv a\mod 3+b\mod 3+c\mod 3 (a+b+c)mod3≡amod3+bmod3+cmod3.
Then we think greater than or equal to 100 100 The number of 100, they must exist 3 3 3 bits m o d 3 \mod 3 Not after mod3 0 0 0 But after discovering this 111 , 112 , 121...222 111,112,121...222 111,112,121... 222 there must be some substring summation after a series of combinations m o d 3 ≡ 0 \mod 3\equiv0 mod3 ≡ 0, then we will be arbitrary, directly before violent treatment 100 100 Just 100.
bool check(int x) {
int p[3];
p[0] = x % 10;
if (p[0] % 3 == 0) return 1;
x /= 10;
if (!x) return 0;
p[1] = x % 10;
if (p[1] % 3 == 0) return 1;
if ((p[0] + p[1]) % 3 == 0) return 1;
x /= 10;
if (!x) return 0;
p[2] = x;
if (p[2] % 3 == 0) return 1;
if ((p[0] + p[2]) % 3 == 0 || (p[1] + p[2]) % 3 == 0 || (p[0] + p[1] + p[2]) % 3 == 0)
return 1;
return 0;
}
int solve() {
ll l = read(), r = read();
if (r <= 100) {
int x = 0;
for (int i = l; i <= r; ++i) {
x += check(i);
}
print(x);
}
else {
ll res = r - l + 1;
for (ll i = l; i <= 100; ++i) {
res -= !check(i);
}
print(res);
}
return 1;
}
G,Game of Swapping Numbers
General idea of the topic
Given equal length sequence A , B A,B A. B, you have to exchange k ( 0 ≤ k ≤ 1 0 8 ) k(0\le k\le 10^8) k(0 ≤ k ≤ 108) times A A Two different numbers in A sequence, output the final ∑ i = 1 n ∣ A i − B i ∣ \sum\limits_{i=1}^n|A_i-B_i| i=1 Σ n ∣ Ai − Bi ∣ what is the maximum.
2 ≤ n ≤ 5 ∗ 1 0 5 , − 1 0 8 ≤ A i , B i ≤ 1 0 8 2\le n\le 5*10^5, -10^8\le A_i,B_i\le 10^8 2≤n≤5∗105,−108≤Ai,Bi≤108
Solution
Test site: greed
We assume that the sequence A = { 0 , 2 , 5 } , B = { 1 , 3 , 4 } A=\{0,2,5\},B=\{1,3,4\} A={0,2,5},B={1,3,4}, then we sum the absolute values to A , B A,B A. Set B assigns signs and ensures that the number of signs is equal when the final two sets are calculated together, and the number of signs in a single set can be different.
So for the above, our optimal allocation strategy is A = { − 0 , − 2 , + 5 } , B = { − 1 , + 3 , + 4 } A=\{-0,-2,+5\},B=\{-1,+3,+4\} A = {− 0, − 2,+5},B = {− 1, + 3, + 4}. It can be seen that the optimal solution is the front n n n large positive sign, front n n n small minus sign.
We can also find that for n > 2 n>2 n> At 2, k > k> k> Minimum number of times and sum of optimal solutions k = k= k = the minimum number of times of the optimal solution is consistent, because at this time A A There must be A minimum in A 2 2 2) the same symbols. We only need to exchange the same grinding times of these two symbols, n = 2 n=2 Judge when n=2 k k The parity of k is sufficient.
Next, let's look at how to build the best possible solution. First, we can get the initial positive sign set and negative sign set, and we exchange each time A A Two numbers in A , can be adjusted 2 2 2. For the symbols of numbers, turn a positive sign into a negative sign and a negative sign into a positive sign. It is obvious that to optimize the answer, we must first exchange the symbols of the largest negative sign and the smallest positive sign until all numbers or numbers are processed k k k exhausted.
int a[N], b[N];
int maxi[N], mini[N];
int solve() {
n = read(), k = read();
rep(i, 1, n) a[i] = read();
rep(i, 1, n) b[i] = read();
if (n == 2) {
if (k & 1) print(abs(a[1] - b[2]) + abs(a[2] - b[1]));
else print(abs(a[1] - b[1]) + abs(a[2] - b[2]));
}
else {
ll sum = 0;
for (int i = 1; i <= n; ++i) {
maxi[i] = max(a[i], b[i]);
mini[i] = min(a[i], b[i]);
sum += abs(a[i] - b[i]);
}
sort(maxi + 1, maxi + 1 + n); // The small positive sign set starts to pick
sort(mini + 1, mini + 1 + n, greater<int>()); // Negative sign set big start pick
for (int i = 1; i <= n && i <= k; ++i) {
if (mini[i] > maxi[i]) {
sum += 2 * (mini[i] - maxi[i]);
}
else break;
}
print(sum);
}
return 1;
}
H,Hash Function
General idea of the topic
Give a length of n ( 1 ≤ n ≤ 5 e 5 ) n(1\le n\le 5e5) If n(1 ≤ n ≤ 5e5) sequences are different from each other, you should select one S e e d Seed Seed let n n n numbers in modulus S e e d Seed Under the premise of Seed, they are different from each other to find the minimum S e e d Seed Seed.
Solution
Test points: polynomial multiplication, convolution F F T FFT FFT
Firstly, a simplification problem is considered and a sequence is given a 1 , a 2 . . . a n a_1,a_2...a_n a1,a2... an, a sequence b 1 , b 2 . . . b n b_1,b_2...b_n b1,b2... bn# if you can choose any two numbers a i + b j a_i+b_j ai + bj , I want you to judge whether this number exists and how you can deal with it. First of all, don't consider opening the bucket O ( n ) O(n) O(n) practice, we require O ( n log n ) O(n\log n) O(nlogn) processing, it is obvious that we write the generating function of this sequence.
P 1 = x a 1 + x a 2 . . . + x a n P_1=x^{a_1}+x^{a_2}...+x^{a_n} P1=xa1+xa2...+xan
P 2 = x b 1 + x b 2 . . . + x b n P_2=x^{b_1}+x^{b_2}...+x^{b_n} P2=xb1+xb2...+xbn
Obviously we're facing a , b a,b a. After B convolution, we can get all the results x a i + b j x^{a_i+b_j} The coefficient in front of xai + bj , can judge whether this number exists.
So back to this question, I want to choose one S e e d Seed Seed allows all numbers to have no hash conflict, that is, there are no following formulas.
a i m o d S e e d = a j m o d S e e d a_i\mod Seed= a_j\mod Seed aimodSeed=ajmodSeed
a i m o d S e e d − a j m o d S e e d = 0 a_i\mod Seed- a_j\mod Seed=0 aimodSeed−ajmodSeed=0
( a i − a j ) m o d S e e d = 0 (a_i- a_j)\mod Seed=0 (ai−aj)modSeed=0
Then the problem becomes that I want to find one S e e d Seed Seed made him not any one a i − a j a_i-a_j Divisor of ai − aj.
Above, we know how to solve it quickly a i + b j a_i+b_j The coefficient of ai + bj , is the same as subtraction here, using an offset P P P just turn a negative number into a positive number.
Next, face a i a_i ai} and P − a i P-a_i P − ai once F F T FFT FFT, and then enumerate the smallest factor.
#include <bits/stdc++.h>
using namespace std;
#define all(__vv__) (__vv__).begin(), (__vv__).end()
#define endl "\n"
#define pai pair<int, int>
#define ms(__x__,__val__) memset(__x__, __val__, sizeof(__x__))
#define debug(x) cout << #x << ":" << x << '\n'
typedef tuple<int, int> tup;
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll read() { ll s = 0, w = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1; for (; isdigit(ch); ch = getchar()) s = (s << 1) + (s << 3) + (ch ^ 48); return s * w; }
inline void print(ll x, int op = 10) { if (!x) { putchar('0'); if (op) putchar(op); return; } char F[40]; ll tmp = x > 0 ? x : -x; if (x < 0)putchar('-'); int cnt = 0; while (tmp > 0) { F[cnt++] = tmp % 10 + '0'; tmp /= 10; } while (cnt > 0)putchar(F[--cnt]); if (op) putchar(op); }
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1) ans *= a; b >>= 1; a *= a; } return ans; } ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
const int dir[][2] = { {0,1},{1,0},{0,-1},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1} };
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF64 = 0x3f3f3f3f3f3f3f3f;
const int N = (2097152) + 7; // 2^21
ll n, m;
const double PI = acos(-1);
struct cp {
double r, i; cp(double _r = 0, double _i = 0) { r = _r, i = _i; }
cp operator+(const cp& x)const { return cp(r + x.r, i + x.i); }
cp operator-(const cp& x)const { return cp(r - x.r, i - x.i); }
cp operator*(const cp& x)const { return cp(r * x.r - i * x.i, r * x.i + i * x.r); }
cp conj() { return cp(r, -i); }
}a[N], b[N];
int c[N], rev[N], limit;
double p1[N], p2[N];
const int P = 500001;
void FFT(cp* a, int inv) {
for (int i = 0; i < limit; ++i) {
if (i < rev[i])swap(a[i], a[rev[i]]);
}
for (int mid = 1; mid < limit; mid <<= 1) {
cp w1(cos(PI / mid), inv * sin(PI / mid));
for (int i = 0; i < limit; i += mid * 2) {
cp wk(1, 0);
for (int j = 0; j < mid; ++j, wk = wk * w1) {
cp x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
if (inv == -1) {
for (int i = 0; i < limit; ++i)
c[i] = a[i].r / limit + 0.5;
}
}
bool vis[N];
bool check(int x) {
for (int i = x; i <= P; i += x) {
if (vis[i]) return 0;
}
return 1;
}
int solve() {
n = read();
for (int i = 1; i <= n; ++i) {
int x = read();
a[x].r = 1;
b[P - x].r = 1;
}
int bit = 0;
while (1 << bit < P * 2) ++bit;
limit = 1 << bit;
for (int i = 0; i < limit; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
FFT(a, 1); FFT(b, 1);
for (int i = 0; i < limit; ++i) a[i] = a[i] * b[i];
FFT(a, -1);
for (int i = 0; i < limit; ++i) {
if (c[i] > 0) vis[abs(i - P)] = 1;
}
for (int i = n; i < P + 1; ++i) {
if (check(i)) return print(i), 1;
}
return 1;
}
int main() {
//int T = read(); rep(_, 1, T)
{
solve();
//cout << (solve() ? "YES" : "NO") << endl;
}
return 0;
}
I,Increasing Subsequence
General idea of the topic
Give a length of n ( 1 ≤ n ≤ 5000 ) n(1\le n\le 5000) Arrangement of n(1 ≤ n ≤ 5000) p i p_i pi, two players choose the number in turn. If a player chooses the number p i p_i pi , then the backhand can only select one j j j. And meet j > i , p j > p i j>i,p_j>p_i j>i,pj>pi. Ask the expected number of games in this game.
Solution
Test site: expectation d p dp dp
We define f [ i ] [ j ] f[i][j] f[i][j] was the last choice i i i this number, choose it next time j j j is the expectation of this number.
Then the state transition equation is: f [ i ] [ j ] = ∑ k = j + 1 n ( f [ j ] [ k ] + 1 ) c n t \displaystyle f[i][j]=\frac{\sum\limits_{k=j+1}^{n} (f[j][k]+1)}{cnt} f[i][j]=cntk=j+1 Σ n (f[j][k]+1), where the legal transfer superposition, c n t cnt cnt # is the number of legal transfers, + 1 +1 +1 ¢ represents a multi-step operation.
So, after we get the state transition equation, we enumerate the last selection in reverse order i i i this number, and then traverse from back to front p j p_j pj.
If p j > i p_j>i pj > I ﹐ description f [ i ] [ p j ] f[i][p_j] f[i][pj] is a reasonable transfer cumulative sum;
If p j < i p_j<i pj < I description f [ p j ] [ i ] f[p_j][i] f[pj] [i] should be calculated once.
In the end, our answer is ∑ i = 1 n f [ 0 ] [ i ] n \displaystyle \frac{\sum\limits_{i=1}^n f[0][i]}{n} ni=1 Σ n f[0][i], the division involved is calculated by inverse element, which can be preprocessed by linear inverse element.
const int MOD = 998244353;
const int N = 5e3 + 7;
ll n, m;
ll p[N], inv[N];
ll f[N][N]; // f[i][j] expectation of selecting I last time and j next time
int solve() {
n = read();
inv[0] = inv[1] = 1;
for (int i = 2; i <= n; ++i)
inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
for (int i = 1; i <= n; ++i) p[i] = read();
for (int i = n; i >= 1; --i) { // i was chosen last time
ll sum = 0, cnt = 0; // The sum of all expectations that can be selected after sum and the number of times that can be selected after cnt
for (int j = n; j >= 0; --j) {
if (p[j] > i) {
++cnt;
sum += f[i][p[j]];
sum %= MOD;
}
else if (p[j] < i) {
f[p[j]][i] = 1;
f[p[j]][i] += sum * inv[cnt] % MOD;
f[p[j]][i] %= MOD;
}
}
}
ll res = 0;
for (int i = 1; i <= n; ++i)
res = (res + f[0][i]) % MOD;
print(res * inv[n] % MOD);
return 1;
}
J,Journey among Railway Stations
General idea of the topic
You have one n ( 1 ≤ n ≤ 1 0 6 ) n(1\le n\le 10^6) For the train route with n(1 ≤ n ≤ 106) points, the opening time of each railway station is [ u i , v i ] [u_i,v_i] [ui, vi], from page i i i train station to No i + 1 i+1 What is the time of i+1 railway station d i d_i di.
The title is 3 3 3) operations, which can modify the position of a point [ u i , v i ] [u_i,v_i] [ui, vi], or modify d i d_i di, the third operation is to ask you from i i Of point i x x Whether you can pass the last railway station at time x. The standard adopted by the railway station is that you can come and wait in advance, but you are not allowed to be late.
Solution
Test site: data structure (line segment tree)
I think the official solution is very good. I'll post their solution and my own code, but I still don't know why my code is controlled by parameters ( r t , l , r ) (rt,l,r) (rt,l,r) line segment tree number, left boundary of control, right boundary of control, can only pass forever 28 % 28\% About 28%, put ( l , r ) (l,r) (l,r) placed in the segment tree s t r u c t struct You can control it in struct A C . . . AC... AC... Maybe the space for this question is not enough, which leads to the explosion of the stack during backtracking?

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define all(__vv__) (__vv__).begin(), (__vv__).end()
#define endl "\n"
#define pai pair<ll, ll>
#define ms(__x__,__val__) memset(__x__, __val__, sizeof(__x__))
#define rep(i, sta, en) for(int i=sta; i<=en; ++i)
#define repp(i, sta, en) for(int i=sta; i>=en; --i)
#define debug(x) cout << #x << ":" << x << '\n'
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll read() { ll s = 0, w = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1; for (; isdigit(ch); ch = getchar()) s = (s << 1) + (s << 3) + (ch ^ 48); return s * w; }
inline void print(ll x, int op = 10) { if (!x) { putchar('0'); if (op) putchar(op); return; } char F[40]; ll tmp = x > 0 ? x : -x; if (x < 0)putchar('-'); int cnt = 0; while (tmp > 0) { F[cnt++] = tmp % 10 + '0'; tmp /= 10; } while (cnt > 0)putchar(F[--cnt]); if (op) putchar(op); }
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1) ans *= a; b >>= 1; a *= a; } return ans; } ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
const int dir[][2] = { {0,1},{1,0},{0,-1},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1} };
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF64 = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 7;
ll u[N], v[N], d[N], suf[N];
struct node {
int l, r, mid;
ll uma, vmi, lazy;
bool ok;
}tree[N << 2];
#define ls x<<1
#define rs x<<1|1
#define MID (L+R>>1)
void merge(node& x, node lson, node rson) {
x.uma = max(lson.uma, rson.uma);
x.vmi = min(lson.vmi, rson.vmi);
x.ok = (lson.ok && rson.ok && lson.uma <= rson.vmi);
}
void build(int x, int l, int r, int L, int R) {
tree[x] = { l,r,(l + r) >> 1,0,0,0,0 };
if (l == r) {
tree[x].uma = u[l];
tree[x].vmi = v[l];
tree[x].ok = 1;
tree[x].lazy = 0;
return;
}
int mid = tree[x].mid;
assert(l == L);
assert(r == R);
assert(MID == mid);
build(ls, l, mid, L, MID);
build(rs, mid + 1, r, MID + 1, R);
merge(tree[x], tree[ls], tree[rs]);
}
void solve(int x, ll k) {
tree[x].uma += k;
tree[x].vmi += k;
tree[x].lazy += k;
}
void pd(int x) {
if (tree[x].lazy) {
solve(ls, tree[x].lazy);
solve(rs, tree[x].lazy);
tree[x].lazy = 0;
}
}
void modify(int x, int l, int r, ll k, int id) {
if (l <= tree[x].l && tree[x].r <= r) {
if (id == 1) solve(x, k);
else if (id == 2) tree[x].uma += k;
else if (id == 3) tree[x].vmi += k;
return;
}
pd(x);
int mid = tree[x].mid;
if (l <= mid) modify(ls, l, r, k, id);
if (r > mid) modify(rs, l, r, k, id);
merge(tree[x], tree[ls], tree[rs]);
}
node query(int x, int l, int r) {
if (l <= tree[x].l && tree[x].r <= r) {
return tree[x];
}
int mid = tree[x].mid;
pd(x);
node ans = { 0,0,0,0,0,0,0 };
if (r <= mid) ans = query(ls, l, r);
else if (l > mid) ans = query(rs, l, r);
else merge(ans, query(ls, l, mid), query(rs, mid + 1, r));
return ans;
}
void solve() {
int n = read();
rep(i, 1, n) u[i] = read();
rep(i, 1, n) v[i] = read();
rep(i, 1, n - 1) d[i] = read();
suf[n] = 0;
repp(i, n - 1, 1) suf[i] = suf[i + 1] + d[i];
rep(i, 1, n) u[i] += suf[i], v[i] += suf[i];
build(1, 1, n, 1, n);
int Q = read(), op, l, r, pos, w;
while (Q--) {
op = read();
if (op == 0) {
l = read(), r = read();
if (query(1, l, r).ok) {
puts("Yes");
}
else {
puts("No");
}
}
else if (op == 1) {
pos = read(), w = read();
modify(1, 1, pos, w - d[pos], 1); // Differential modification
d[pos] = w;
}
else if (op == 2) {
pos = read(), l = read(), r = read();
modify(1, pos, pos, suf[pos] - u[pos] + l, 2);
modify(1, pos, pos, suf[pos] - v[pos] + r, 3);
u[pos] = suf[pos] + l;
v[pos] = suf[pos] + r;
}
}
}
signed main() {
int T = read(); rep(_, 1, T)
{
solve();
}
return 0;
}
K,Knowledge Test about Match
General idea of the topic
Randomly generate a weight range of $0\to n-1 of order column , you want use The sequence you want to use You want to use 0\to n-1 go and it Horse match , Horse match letter number yes To match it, the matching function is To match it, the matching function is sqrt $. It is required that the average deviation from the standard value shall not exceed 4 % 4\% 4%.
Solution
There is no test site for this question... You can see a few words randomly generated, and the supplementary questions after the game began to mess around.
So the solution to this problem comes from water
const int N = 1e3 + 7;
ll n, m;
int p[N];
double sqr[N];
int solve() {
n = read();
rep(i, 0, n - 1) p[i] = read();
sort(p, p + n);
int t = 5;
while (t--) {
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (sqr[abs(i - p[i])] + sqr[abs(j - p[j])] > sqr[abs(i - p[j])] + sqr[abs(j - p[i])]) {
swap(p[i], p[j]);
}
}
}
}
rep(i, 0, n - 1) print(p[i], " \n"[i + 1 == n]);
return 1;
}
int main() {
rep(i, 1, N - 1) sqr[i] = sqrt(i);
int T = read(); rep(_, 1, T)
{
solve();
//cout << (solve() ? "YES" : "NO") << endl;
}
return 0;
}