1. Title

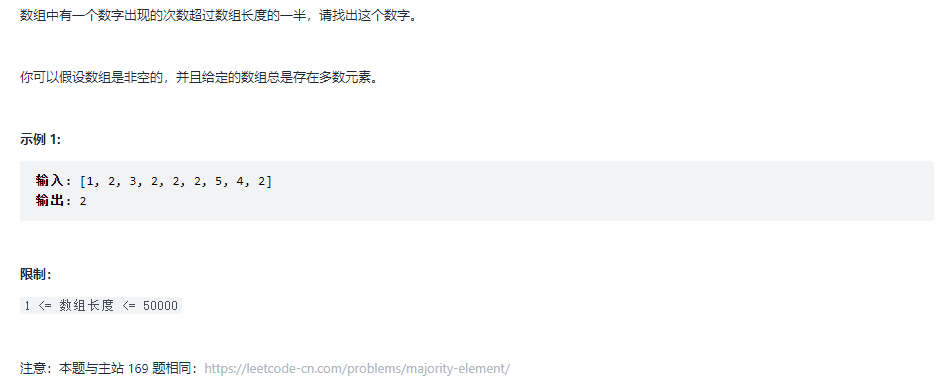
2. Ideas

(1) Quick sort

• When the array is ordered, the number that occurs more than half the length of the array must be the number in the middle of the array.

(2) Hash table (semi statistical)

• Use the hash table to count the number of occurrences of each number.
• You can judge whether the number of occurrences of each number has exceeded half of the length of the array while counting. If it exceeds half, you can return it directly.
• Since the number of occurrences exceeding half of the array length is returned, the number of occurrences of the target number must not exceed half of the array length when counting the first half of the array. Therefore, it is not necessary to judge when counting the first half of the array to improve efficiency.

(3) Hash table (full statistics)

• The idea is basically the same as that in (2). You can also find out the number that occurs more than half the length of the array after counting all the times.
• In extreme cases, (3) is more efficient than (2).

(4) Divide and conquer

• The basic idea is that when a number appears more than half the length of the array, the number is at least the mode of one of the left or right half of the array.
• If the array length is 1, the mode is its unique value and can be returned directly; If the length of the array is greater than 1, the mode is the mode with more occurrences in the left and right parts.

(5) Moore voting method

• If the mode represents the total number of votes + 1 and other numbers represent the total number of votes - 1, the total number of votes must be greater than 0 after counting the whole array.
• Assuming that the mode is the first number, traverse from front to back. If the number encountered is equal to the mode, the total number of votes is + 1, otherwise the total number of votes is - 1.
• If the total number of votes in the previous interval of the array is 0, the total number of votes in the subsequent interval must be greater than 0. Therefore, you can reset the mode to the first number in the subsequent interval and restart statistics.

3. Code

import java.util.*;

public class Test {
    public static void main(String[] args) {
        int[] ints = {3, 2, 3};
        Solution1 solution = new Solution1();
        System.out.println(solution.majorityElement(ints));
    }
}

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

class Solution1 {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        int minCount = nums.length / 2;
        for (int i = 0; i < minCount; i++) {
            if (map.containsKey(nums[i])) {
                map.put(nums[i], map.get(nums[i]) + 1);
            } else {
                map.put(nums[i], 1);
            }
        }
        for (int i = minCount; i < nums.length; i++) {
            if (map.containsKey(nums[i])) {
                map.put(nums[i], map.get(nums[i]) + 1);
            } else {
                map.put(nums[i], 1);
            }
            if (map.get(nums[i]) > minCount) {
                return nums[i];
            }
        }
        return nums[0];
    }
}

class Solution2 {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            if (map.containsKey(num)) {
                map.put(num, map.get(num) + 1);
            } else {
                map.put(num, 1);
            }
        }
        int minCount = nums.length / 2;
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            if (entry.getValue() > minCount) {
                return entry.getKey();
            }
        }
        return nums[0];
    }
}

class Solution3 {
    public int majorityElement(int[] nums) {
        return majorityElementRec(nums, 0, nums.length - 1);
    }

    private int majorityElementRec(int[] nums, int low, int high) {
        if (low == high) {
            return nums[low];
        }
        int midIndex = (high - low) / 2 + low;
        int left = majorityElementRec(nums, low, midIndex);
        int right = majorityElementRec(nums, midIndex + 1, high);
        if (left == right) {
            return left;
        }
        int leftCount = countInRange(nums, left, low, high);
        int rightCount = countInRange(nums, right, low, high);
        return leftCount > rightCount ? left : right;
    }

    private int countInRange(int[] nums, int num, int low, int high) {
        int count = 0;
        for (int i = low; i <= high; i++) {
            if (nums[i] == num) {
                count++;
            }
        }
        return count;
    }
}

class Solution4 {
    public int majorityElement(int[] nums) {
        int result = nums[0];
        int count = 0;
        for (int num : nums) {
            if (count == 0) {
                result = num;
            }
            count += num == result ? 1 : -1;
        }
        return result;
    }
}