catalogue
Parity tree
describe
If a binary tree satisfies the following conditions, it can be called a parity tree:
The subscript of the layer where the root node of the binary tree is located is 0, the subscript of the layer where the child node of the root is located is 1, the subscript of the layer where the grandson node of the root is located is 2, and so on.
The values of all nodes on the even subscript layer are odd integers, increasing strictly from left to right
The values of all nodes on the odd subscript layer are even integers, decreasing strictly from left to right
Give you the root node of the binary tree. If the binary tree is a parity tree, return true; otherwise, return false.
Example 1
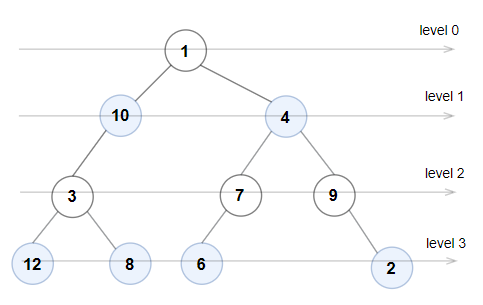
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: the node values of each layer are: 0 Layer:[1] 1 Layer:[10,4] 2 Layer:[3,7,9] 3 Layer:[12,8,6,2] Since the node values on layers 0 and 2 are odd and strictly increasing, while the node values on layers 1 and 3 are even and strictly decreasing, this is a parity tree.
Example 2
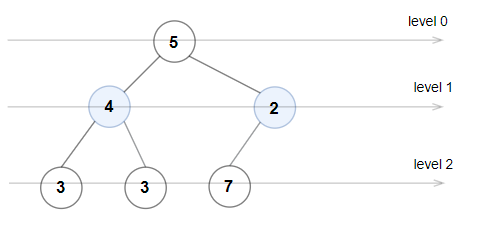
Input: root = [5,4,2,3,3,7] Output: false Explanation: the node values of each layer are: 0 Layer:[5] 1 Layer:[4,2] 2 Layer:[3,3,7] 2 The node value on the layer does not meet the strict increment condition, so this is not a parity tree.
Example 3
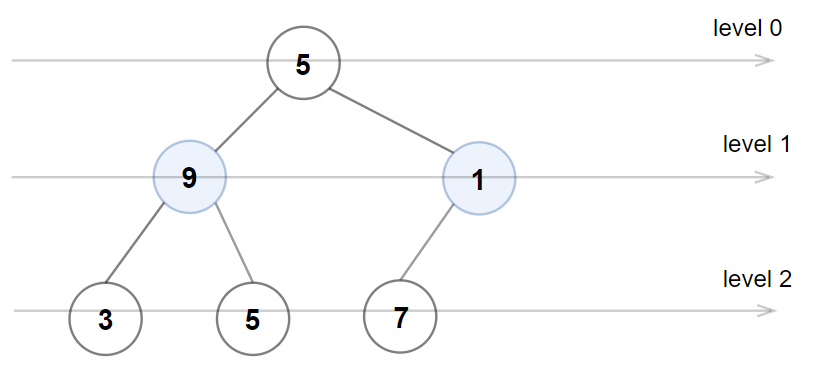
Input: root = [5,9,1,3,5,7] Output: false Explanation: the node value on layer 1 should be even.
Example 4
Input: root = [1] Output: true
Example 5
Input: root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17] Output: true
Tips
- The number of nodes in the tree is in the range [1, 105]
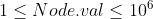
data structure
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}Methods: breadth first search
Since the condition for judging whether a binary tree is a parity tree is for the nodes of the same layer, breadth first search can be used. Each round of search accesses all nodes of the same layer, and only the nodes of this layer will be accessed.
Use queues to store nodes. Initially, the root node is added to the queue. Before each round of search, the nodes in the queue are all nodes in the same layer. Remember that the size of the queue is size. Only size nodes are accessed in this round of search, which can ensure that all nodes in the same layer are accessed in this round of search. In the search process, the non empty child nodes of the nodes of the current layer are successively added to the queue for the search of the next layer.
To judge whether a binary tree is a parity tree, two conditions need to be considered: the parity of node values and the monotonicity of node values. Both conditions are determined by the parity of layer subscripts. Therefore, it is necessary to maintain the searched layer subscript and the previous node value for each layer search.
If the subscript of the current layer is even, the values of all nodes of the current layer are required to be odd, and the node values are strictly increased from left to right. If the node value is even, or the current node value is less than or equal to the previous node value, the binary tree must not be a parity tree.
If the subscript of the current layer is odd, the values of all nodes of the current layer are required to be even, and the node values are strictly decreasing from left to right. If the node value is odd, or the current node value is greater than or equal to the previous node value, the binary tree must not be a parity tree.
If all nodes of a binary tree meet the conditions of a parity tree, the binary tree is a parity tree.
class Solution {
public boolean isEvenOddTree(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
queue.offer(root);
int level = 0;
while (!queue.isEmpty()) {
int size = queue.size();
int prev = level % 2 == 0 ? Integer.MIN_VALUE : Integer.MAX_VALUE;
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
int value = node.val;
if (level % 2 == value % 2) {
return false;
}
if ((level % 2 == 0 && value <= prev) || (level % 2 == 1 && value >= prev)) {
return false;
}
prev = value;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
level++;
}
return true;
}
}