CJB
Cop! Run!!
la guy's problem, la guy's problem these days is not white
Title Description
from Crypto.Util.number import *
from flag import flag
n = 1 << 8
p = getPrime(n)
print(p)
P.<t> = PolynomialRing(Zmod(p))
f = t * t + randrange(p)
print(f)
x = [randrange(p)]
x += [f(x[0])]
print([x_ >> (n - ceil(5 * n / 7)) for x_ in x])
flag = bytes_to_long(flag)
y = f(x[-1])
for i in range(7):
y = f(y)
flag ^^= int(y)
print(flag)
'''
92946459607669937513774102250057295249718593723232674702212854287358873135783
t^2 + 43844336985235863734419631630425915388298791521868754583032904718644333115590
[3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]
193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
'''
hint
Brad Pitt & Angelina Jolie love each other hard in some movie.
Problem solving ideas
Cop appears in the title. I guess it's CopperSmith; It was learned from hint that CopperSmith did not run away from the 2005 film Mr Smith & Mrs Smith
Look at the code first. The code is very short. Obviously, it only requires the first two items of X, and all problems will be solved. In other words, as long as you know x[1], you can find y, and then encrypt or decrypt according to the nature of XOR
What we know is that x shifts 73 bits to the right, which obviously requires low bits. Naturally, you can think of the idea of equation, set several variables, and then solve the equation according to the equation. Because I've been in touch with the application of copper Smith in RSA, smal in sage_ Roots is based on CopperSmith
Here is a brief introduction to copper Smith, which is extracted from the CTF Wiki
CopperSmith Fundamentals ¶
Coppersmith related attacks and Don Coppersmith Closely related, he proposed a polynomial time method for finding all small integer roots of modular polynomials (univariate, bivariate, and even multivariate variables).
Here we mainly introduce single variable, assuming
- The modulus is n, and N has a factor b ≥ N β , 0 < β ≤ 1 b≥N^β,0<β≤1 b≥Nβ,0<β≤1
- The degree of polynomial F is δ δ δ
Then this method can be used in O ( c δ 5 l o g 9 ( N ) ) O(cδ^5log^9(N)) O(c δ Find all roots of the polynomial within the complexity of 5log9(N)) x 0 x_0 x0, here we ask ∣ x 0 ∣ < c N β 2 δ |x_0|<cN^\frac{β^2}{δ} ∣x0∣<cNδβ2.
In this problem, our goal is to find all the roots of polynomials in the sense of module N. this problem is considered to be complex. Coppersmith method is mainly through Lenstra–Lenstra–Lovász lattice basis reduction algorithm (LLL) method found
- Has the same root as the polynomial x 0 x_0 x0
- Smaller coefficient
- The definition field is an integer field
Because it is simple to find the root of the polynomial in the integer field (Berlekamp – Zassenhaus), we get the integer root of the original polynomial in the modular sense.
So the key question is how to convert f to g? Howgrave Graham gives an idea

That is, we need to find a polynomial g with "smaller coefficients", that is, the following conversion method
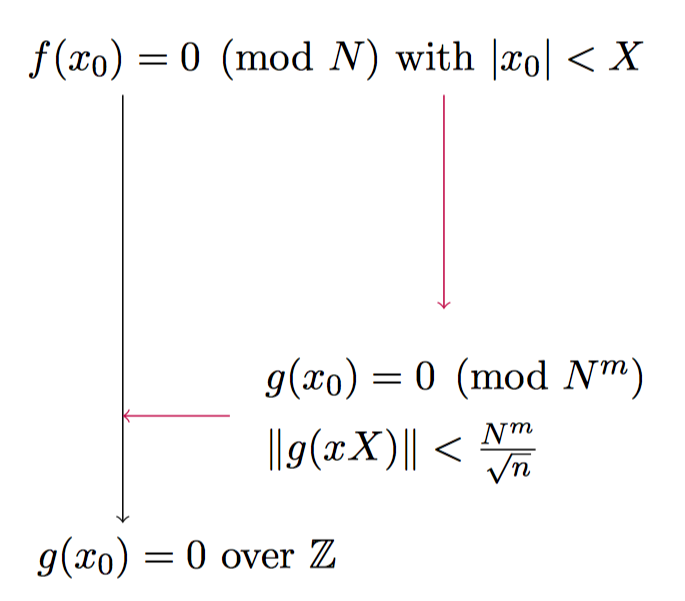
In LLL algorithm, two points are very useful
- Only the integer linear transformation is performed on the original basis vector, which can make us still use the original basis vector when we get g x 0 x_0 x0 is the root.
- The module length of the generated new basis vector is bounded, which allows us to use howgrave Graham theorem.
On this basis, we can construct a polynomial family g.
For more details, please search by yourself. At the same time, this part will be constantly updated.
It should be noted that due to the constraint of Coppersmith root, the application in RSA is often only applicable to e small cases.
In conclusion, CopperSmith can be used for univariate or multivariate polynomials
Back to the topic, I made a preliminary attempt. Under the guidance of master Shang, I wrote the first polynomial, set X_ The lower 73 bit of [0] is k
f
(
x
_
[
0
]
<
<
73
+
k
)
>
>
73
=
x
_
[
1
]
f(x\_[0]<<73+k)>>73=x\_[1]
f(x_[0]<<73+k)>>73=x_[1]
It's a univariate polynomial about k, and then we try to solve it
la guy's blog has scripts to solve monism and pluralism
#Sage
#unit
PR.<x> = PolynomialRing(Zmod(n))
f = (a + x)^e - c
root = f.small_roots(X=2^256, beta=1)[0] # find root < 2^256 with factor = n
#multivariate
load('coppersmith.sage')
P.<x, y> = PolynomialRing(GF(p))
f = 2^170 * a^2 + 2^86 * a * x + x^2 - 2^85 * b + c - y
roots = coron(f, X=2^85, Y=2^85, k=1, debug=True)[0]
x, y = roots
Changed it
p = 92946459607669937513774102250057295249718593723232674702212854287358873135783 Fp = Zmod(p) pi = 43844336985235863734419631630425915388298791521868754583032904718644333115590 x_ = [3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392] P.<t> = PolynomialRing(Fp) f = t * t + pi PR.<k> = PolynomialRing(Fp) s = f(x_[0]*2^73 + k)//2*73-x_[1] root = s.small_roots(X=2^73, beta=1)[0]
emmmmm has several problems. First, it moves to the right like this. It doesn't know whether it is in or not, and then it always reports an error that goes beyond the boundary

After trying and some equivalent alternatives failed, I thought of adding another variable; First, the representation is clearer and eliminates the uncertainty of right displacement. Second, there are scripts for solving multivariate polynomials in la Lao's blog
If you can't solve it, add another layer. This is what I learned from Jiwang
Let the lower 73 bits of x[0] x[1] be k0 and k1, and the written equation is
f
(
x
_
[
0
]
<
<
73
+
k
0
)
=
x
_
[
1
]
<
<
73
+
k
1
f(x\_[0]<<73+k_0)=x\_[1]<<73+k_1
f(x_[0]<<73+k0)=x_[1]<<73+k1
Complete the tampering of the script, this coppersmith Sage from https://github.com/mimoo/RSA-and-LLL-attacks , also from la guy's blog; la guy yyds
load("coppersmith.sage")
p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
pi = 43844336985235863734419631630425915388298791521868754583032904718644333115590
x_ = [3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]
c = 193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
PR.<t> = PolynomialRing(Fp)
f = t * t + pi
PR.<k0, k1> = PolynomialRing(Fp)
s = f(x_[0]*2^73 + k0)-x_[1]*2^73-k1
roots = coron(f, X=2^85, Y=2^85, k=1, debug=True)[0]
emmmmm conron is not defined. After looking at the source code in github, I really can't find this function; Then we are not sure whether the constructed polynomial is solvable, so we can't do it

There is a function in this github, but it feels that it is used for RSA type topics
When I got up in the morning, I studied this topic again with a try attitude; It's endless search. The ability to collect information still needs to learn from master Shang
Then I found the original question

It was the title of zer0pts CTF three months ago. It seems that this is the meaning of brushing more questions. At that time, Shunteng touched melon and found master Joseph's blog. This master is a god man. Many things were found from him before, tqql
Then he changed his script to make it. In addition to some derivation (I thought oh, I see, but later found that I expanded mine), of course, the most important thing is that he provided a github link for coppersmith to find the small root function
import itertools def small_roots(f, bounds, m=1, d=None): if not d: d = f.degree() R = f.base_ring() N = R.cardinality() f /= f.coefficients().pop(0) f = f.change_ring(ZZ) G = Sequence([], f.parent()) for i in range(m+1): base = N^(m-i) * f^i for shifts in itertools.product(range(d), repeat=f.nvariables()): g = base * prod(map(power, f.variables(), shifts)) G.append(g) B, monomials = G.coefficient_matrix() monomials = vector(monomials) factors = [monomial(*bounds) for monomial in monomials] for i, factor in enumerate(factors): B.rescale_col(i, factor) B = B.dense_matrix().LLL() B = B.change_ring(QQ) for i, factor in enumerate(factors): B.rescale_col(i, 1/factor) H = Sequence([], f.parent().change_ring(QQ)) for h in filter(None, B*monomials): H.append(h) I = H.ideal() if I.dimension() == -1: H.pop() elif I.dimension() == 0: roots = [] for root in I.variety(ring=ZZ): root = tuple(R(root[var]) for var in f.variables()) roots.append(root) return roots return []
Just change the script a little and it will come out soon
load('coppersmith.sage')
from Crypto.Util.number import long_to_bytes
p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
b = 43844336985235863734419631630425915388298791521868754583032904718644333115590
c = 193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
w0 = 3248642833056635029095920782095626337949113592116495266
w1 = 4883935221919623989344404485025479346028101682781790392
b,w0,w1 = map(Fp, [b,w0,w1])
PR.<k0, k1> = PolynomialRing(Fp)
f = 2^146 * w0^2 + 2^74 * w0 * k0 + k0^2 - 2^73 * w1 + b - k1
roots = small_roots(f, (2^73, 2^73), m=3)[0]
k0, k1 = roots
v0 = 2^73 * w0 + k0
v1 = 2^73 * w1 + k1
PR.<v> = PolynomialRing(Fp)
f = v^2 + b
y = f(v1)
for i in range(7):
y = f(y)
c ^^= int(y)
print(long_to_bytes(c))
When I sorted out WP, I applied this function to my equation yesterday and found it. I'll post the complete script again
load("coppersmith.sage")
from Crypto.Util.number import long_to_bytes
p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
pi = 43844336985235863734419631630425915388298791521868754583032904718644333115590
x_ = [3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]
c = 193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
PR.<t> = PolynomialRing(Fp)
f = t * t + pi
PR.<k0, k1> = PolynomialRing(Fp)
s = f(x_[0]*2^73 + k0)-x_[1]*2^73-k1
roots = small_roots(s, (2^73, 2^73), m=3)[0]
k0, k1 = roots
v0 = 2^73 * x_[0] + k0
v1 = 2^73 * x_[1] + k1
y = f(v1)
for i in range(7):
y = f(y)
c ^^= int(y)
print(long_to_bytes(c))
So we have done more than half of the derivation on master jo's blog, but we need to implement a function
I learned a lot. Through this question, I realized that in the future, in the Crypto direction, I must immediately follow up new question types and visit github more. I'm lucky enough to understand some principles and try to realize them by myself. Now it is true that tcl, a previously implemented playfair, made mistakes when trying to run today
Drifting bottles floating from the other side of the sea
The topic of master Chunge was worked out by a second master in our group at that time
Title Description
On the other side of the sea, a drifting bottle floated over and stopped on the beach. You pick it up, but you don't know what's written on the paper in the drifting bottle.
ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 1O3 FU3 RU RUP EJ/ XJ4 S06 54 284 Q/6 J0 , 5J3 VU04 T;6 2J4 431 EJ/ XU3 . Y4 1O3 D9 G3 S06 VU/6 , U VM4 RU/ EJI4 RU XJ/6 G4 , VUP 1O3 G4 , W96 1O3 G4 , WL6 M06 G4 , VUP 5J6 VU04 , VUP 5J6 G4 , AUL6 XU4 VU04 , W96 5J/ G4 , 5; CJ84 VU04 , S06 W.6 VU04 , MP6 XUP6 VU04 , RU8 U4 VU04 , RU8 U4 G4 , W96 S06 G4 , EL VM/6 G4 , QU/6 2J/ VU04 . ZJ6 X94 EK6 2U6 SO4 BJ/6 G4 T QJ6 WL6 1J4 WJ3 QJ6 WL6 QU6 1J4 T QJ6 WL6 2L3 WJ3 QJ6 WL6 QU6 2U6 C04 M3 QUP UP G.3 Y4 AJ3 QUP RU, . FU6 5J/ U.6 M6 XJ4 2J04 RU04 GK4 G6 2U6 M/4 2U4 FM3 2K6 JP4 WU6 , Y94 W96 5J/ G4 M3 5; CJ84 VU04 5 RU0 M06 1P3 U/ E9 G4 S06 1O3 Y.3 VU;4 2U6 ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 CP3 XU4 J94 2U4 G4 T/6 VU04 2J/ VU VU;4 2U6 Y.3 VU;4 , Y4 S06 1J4 1O3 G;4 VU0 RU/ 5; CJ84 VU04 ZP M06 VU; , DJ84 J VU 54 W96 5J/ G4 J4 Z/ FM , J B4 FM 5 C.4 , Y94 VU;4 VU VU/6 54 5; CJ84 VU04 1O3 1J4 2U6 5; CJ84 G4 , U06 J VU ( NJ6 T/ 284 2J4 VU ) VU VU/6 54 5; CJ84 VU04 CK6 AO3 5P4 , 5J03 EK4 RU, RUP4 56 RUL3 2U6 284 J0 , DJ84 M,4 284 2J4 VU RUP4 BJ4 W96 5J/ G4 C93 VU04 2U4 FM . 1U,6 J;4 RU4 183 ZJ6 X94 EK6 M/4 VU WU 94 ZJ3 VU.4 2U6 EK6 G4 1L EJI3 FU3 X96 I6 . VU; 2JO4 M6 5J/ G0 EL 2; TJ EJO CJ86 G4 U3 TJ04 XU06 W96 J0 VU 04 5J3 UL4 284 T/6 G4 JO6 AJ4 2U6 , DL3 XU;6 2L4 QU/6 C/6 2U4 FM Z8 503 , WJ3 2U4 FM3 2K6 2U6 T/6 1P3 M3 1U4 AU03 2J G4 ZJ4 RUP4 2J03 WJ6 WJ/ FUP6 TK XU.6 YL4 T/6 YJ3 N9 , ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 2U6 VM03 VU04 RU, DK4 U4 1U4 D9 1J4 ZP BP6 D.3 T.6 AU4 2U6 2J CJO4 FM 1U/4 RU/ EJI4 VM3 2JI M06 1P3 2U 2J4 D9 Z8 2U6 VU; HJP 2U4 294 .
hint1
The domineering slogan on the Guangzhou railway station: unify the motherland and revitalize China
hint2
North! E04!
Problem solving ideas
Obviously, it's similar to a single table replacement. Then I randomly selected a few to search and found them on github https://github.com/chinese-opendesktop/cin-tables/blob/master/bopomofo.cin As for the first hint, I haven't understood its meaning until now. The second hint is a Taiwanese dialect and Taiwanese Internet language. I praise you for your awesome meaning
github is the control Thesaurus of orthographic phonetic input method, which exactly corresponds to E04! The origin of also echoes the topic
Then tear it by hand. It's too delicious to process data in python
Tear it in half
Formosa Expressway starts from the fund highway in the north and ends at Dapeng Bay in the south. The main line is 431km long. It starts from the north and goes south, passing through Keelung City, Taipei County, Taoyuan County, Hsinchu County, Miaoli County, Taichung County, Changhua County, Nantou County, Yunlin County, Jiayi County, Tainan County, Kaohsiung County and Pingdong county. fu lai ge The content is the first letter splicing of Chinese phonetic alphabet of eating grapes without spitting grape skin.
Another master said that there was some information behind, but one master said that it was too long to directly input the Pinyin initial of this doggerel
Just pass
Then look at the official WP ChunGe Master said that you can use the online website to do it; Just switch the input method. It's strong
In addition, for this problem, don't buckle during the competition. It's good to do it. It's a waste of time to complete it for perfectionism. This is important in the game. You can do it after the game. For example, I wanted to do it all at that time, but now I'm too lazy to do it, doge
The group leader said to give a simple question. Let's think of it a little simpler
xsl
N = 24873777989291448485268365702265085243886872900039809831478881276969311714448924581398692832639705916538111455861057354225427758736198452679468399039512440497290615485190994957684665065261280544484301856860844163436499302230085760545686486398949018187416289923500558688885485672960734334858119391323987554701544773420070317895909846297195832399677291338220818181502181317849952785959097285626009703863257450199781708945715701136683994546852422993684382468187651935055302074609980311161155531603473091857526099148935429447319415714778860215376802270686310782735079899235228731429165106477537031235405221734008734614847 e = 12436888994645724242634182851132542621943436450019904915739440638484655857224462290699346416319852958269055727930528677112713879368099226339734199519756220248645307742595497478842332532630640272242150928430422081718249651115042880272843243199474509093708144961750279344442742836480367167429059695661993777350613653317802356713323129593521588320771616955563426747034967432053960828426250168954828986666929922730060781213890566121107119389060806644531516491192343284701151238691996162679338542186167193568672632227858449997036747029810933106336313085633759799229646747282205612102678724267585967720538082620536177904609 c = 7539424334663709603622451394173266049480031393220309445902319310504736287365860451132752036622339554159799611768328686792828750952551268647863160547774237934958072391797341405165512721597085695555356929495861914056799039140107261439671707574841789330531198534325422015873621769489969596614802282764401661006564546159674397356683650318142728009273827997179696988926599672213482848150751054351595386402597000601684644207559735499031666361222038615475154046453649719203304187309556004660926226182353445661702352380654352874617084419834338343925880593023307238768452509962
E is very big. I tried boneh_durfee, but can't get out; Check the conditions. This e is too big
Then I see it in many hint s
When you stare at the ciphertext, the ciphertext is staring at you.
Wonderful, Nietzsche
When you stare at the ciphertext, plaintext is staring at you. Direct c to byte, then hand quickly took a blood
The Dedication of Suspect M(Unsolved)
Numb, the most numb problem in this game. 8. Master Chunge's question came out every 7 minutes and was the only solution in the audience. I didn't have a clue until the end of the game
Title Description
There is a lot of information about the topic. I gave it to you directly
Problem solving ideas
I sorted out the following clues:
-
It is a dynamic environment that provides compressed package download. There is a binary file named M. the file content is different every time it is reopened, and the size ranges from 2K to 5K; So the flag is basically dynamic
-
The content of flag is the hexadecimal of lowercase letters, separated by a short horizontal in the middle
-
The dedication of suspect X is changed to the depth of suspect M
??? There's an internal smell??? It's burning???
At the beginning, there was no clue. For example, this was one of the downloaded files
222222222qq222222222qqq22222222222qq22222222222222222222222222222222222q2222q222222qq222222222qq2qq2222222222222222222222222qq22222222qqqq2222222qqq222222222222222qqqqqq22222222222222222qq2222222qq222222222222222222qq2qq2222222qq2qq2222222qqqqqq222222222222222222222222qq2222222qqqqqqqq2222qq22222222qqq222222222222qqqqqqqq2222qq2222222qqqqqqqq2222qq22222222qq22222222qq22222222222222222q222222qq2qq2222222qq22222222222qqq22222q222222qq222222222222An2nqq2222A9qqqn222222222An2n22222222222222222222222222222222A92n2A92n2222An2n2222222An2nn2n2222222222222222222222A9q2rn22222A9qqqn2222A9qqqrn222222222222An22qqqn22222222222222A9q2rn2222An2n2222222222222222An2nn2n22222An2nn2n22222An22qqqn222222222222222222222A9q2rn2222Anqqqqq22n2A9q2rn2222A9qqqn2222222222Anqqqqq22n2A9q2rn2222Anqqqqq22n2A9qqrn2222A9qqrn2222A9q2rn2222222222222A92n2222An2nn2n22222An2n22222222A9qqqn22A92n2222An2rn2222qqq222n2n2>qn22An2nqqA222qqqq22n2n2nqqq222222qqq2222qq22qq22qq2222n2>A9Anq>2n222n2n2nqqqq22n2n2nn2n2222222qq222222qq222An2n^n2n222An2nqqA222Anqn2An2n22222222222n2n2nqqA222222qq22222An2n^n2n222n2n2nqqqq22222222222n2n2nn2n2222n2n2nn2n2222n2n2nqqA22222qqq222222222222An2n^n2n222nAqqqAA9A9An2n^n2n22An2nqqA2222222222nAqqqAA9A9An2n^n2n222nAqqqAA9A9An2nAn2n22An2nAn2n22An2n^n2n222222qq222Anq>2n222n2n2nn2n2222n2n2nqqqq22An2nqqA2Anq>2n222nrn22n22A9qqqn22n2n2nA22n2n2>qqn2A9>qqn22n2n22q2rn222A2qqrn2An2nAn2nAn2n22N92n22nAqAn2n222n2n29qqrn22n2n2nn2nq222A9qqrn22A9qqrn2n2nqqq>2n22n2n22qrrn2nAqAAA2Aqq22qqqqqqq22n2nqqqrrn22A9qqrn222n2nqqq>2n222n2n29qqrn22qqqqqqq22n2n2nn2nq222n2n2nn2nq222n2nqqqrrn22A9qqqn22qqqqqqq2n2nqqq>2n222222A92A92nAqP2q2Nq2n2n2>qqn2qqqqqqq22222A92A92n2nqqq>2n222222A92A92n2n2n2n2n2n2n2n2n2n2n2nqqq>2n222A9qqrn2nAqAn2n222n2n2nn2nq222n2n29qqrn2n2n2>qqnnAqAn2n222n2n2rPAn2nqqA222n2n2nq22n2n2nqAAnqq>2rn22n2n2n2n2n2An2n^n2nn2n2nqA2nqA2nN2n2rn2222n2n2n222n2n2n^n2n22n2nqq2>qqnAn22qqA2An22qqA22nAqq>An2n22n2n2n^n2n222AA2Aqn2nAnqqqqqqn22nAn2n^n2nAn2n^n@nq22nAqq>An2n222n2n2n^n2nAnqqqqqqn22n2nqq2>qqn22n2nqq2>qqn22nAn2n^n2nAn2nqqA2Anqqqqqqn2nAqq>An2n222A92A922222An2n^n2n2n2n2nqAAnqqqqqqn22A92A92222nAqq>An2n222A92A92222n2n2nqn2n2n2n2nqn2n2nAqq>An2n2An22qqA2222n2n2n222n2nqq2>qqn22n2n2n^n2n2n2n2nqA222n2n2n22AA92n2n2nqqqqn222n2nqqn22n2nqn2nAnqqqqA222n2nqn2nqnn2nqqqqA2n2nqqq qqqA92nrnqqn2222n2nqn222n2nq>qqA222nAqAnqnqAn2nqqqqnn2nqqqqn222222n2nqn22n2nqqqqA22AnqqqqqqAnAqqqqqqA222n2nqqqqAn2nqqA@nqn222222n2nqn222n2nq>qqAnAqqqqqqA222nAqAnqnqA222nAqAnqnqA222n2nqqqqAn2nqqqqnnAqqqqqqA222222n2nqn2AnqA2222222n2nqqqqA22n2nqn2nAqqqqqqA2AnqA22222222222n2nqn2AnqA2222222n2nqqqqA22n2nqqqqA222222n2nqnn2nqqqqn2222n2nqn222nAqAnqnqA222n2nq>qqA22n2nqn22222n2nqnAnqqA922nAqqqqA2222nAqqA222nAqA22nAqqqA22222nAqAnAqA2nAqqqA222nAqqAAqqA2222nAqqA22222nAqA2222nAqqqA2222222nAqA222nAqqqqA2nAqqqqA2222222nAqA222nAqqqA222nAqqqqqA22222222222222nAqqqA22nAqqAnAqA2222222nAqA2222nAqqqA2222222222222222nAqA22222222nAqA222222nAqqqA22nAqqqqA2222222222222222nAqA2nAA222222222nAqqqA2222nAqA22222222222nAA2222222222222nAqA2nAA222222222nAqqqA2222nAqqqA22222222nAqA2nAqqqqA22222nAqA222222nAqA222222nAqqqA2222nAqA222222nAqAnAqA2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222
According to the existing clues: each dynamic flag is different, 0-9 a-f, all I can think of is

But I tried it with the master in the group. It's not very good whether it's for file md5 or compressed package md5; md4 doesn't work either; In addition, I don't know how to cut the dividing line. I handle it according to the example, and I don't know whether it is right or not. TNL, do you want to fart

At the end of the game, I took away some water problems and stuck the record
36D cup
justShow
hlcgoyfsjqknyifnpd:bcdefghijklmnopqrstuvwxyza
The prompt behind the colon is Caesar's displacement. Move it back to get it
gkbfnxeripjmxhemoc:abcdefghijklmnopqrstuvwxyz
Then I didn't expect playfair, followed by key; Take it to the online website and decrypt it
There is a bit of a dog here, because playfair has only 25 alphabets, usually i instead of j; But it's not here. It hasn't been stated clearly, so it can't come out by default. Because the key is a-z, the alphabet is a-z. there is no need to replace any letters. Just change the parameters
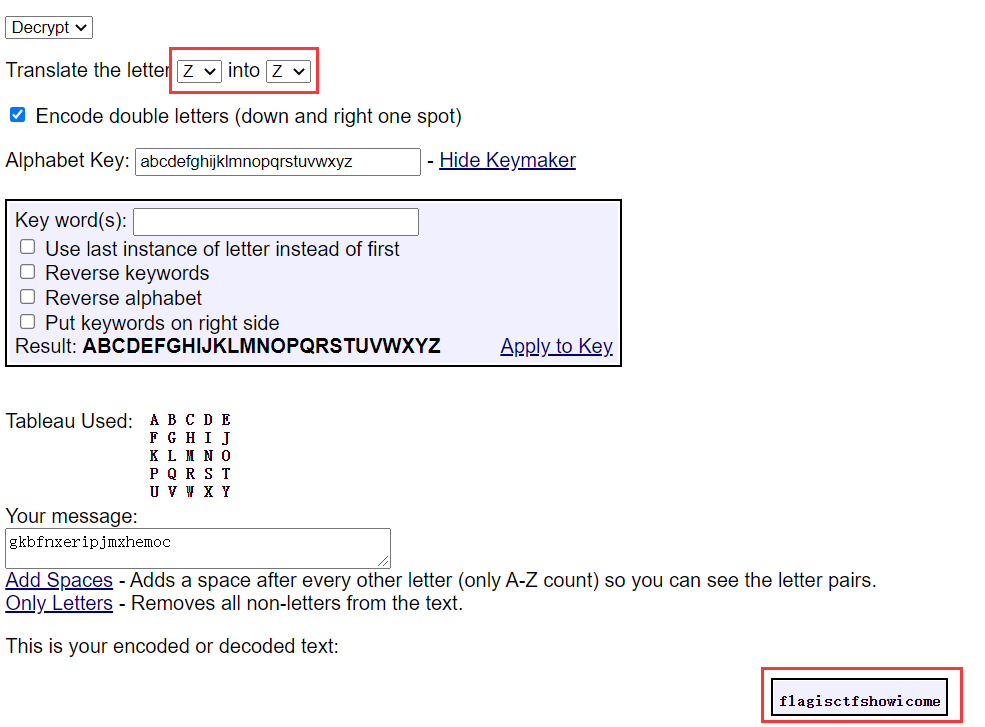
Get flag
flagctfshow{ctfshowicome}
Flying Pigeon biography
Provide attachment download, pub key
TVdJd09HRm1NamMyWkdKak56VTVNekkzTVdZMFpXVTJNVFl5T0Rrek1qUWxNRUZsTW1GbE0yRXlNelV3TnpRell6VXhObU5rWVRReE1qUTVPV0poTTJKbE9TVXdRV0prWlRVeVkySXpNV1JsTXpObE5EWXlORFZsTURWbVltUmlaRFptWWpJMEpUQkJaVEl6WlRBd1ltVXpPV1F6Tm1Zek5EWXlaVFUzTm1FMk4yRTNaamt4T1RrbE1FRXhPR00zT1RJNE5XSTFNVFJqTmpObVl6a3dNelZsTTJZNU1qQmhaVFEzTnlVd1FXUmhORFJrWkRFNU1tUmxabVF4WW1VM09XWTJNMk16TlRCa01qa3lNR05tSlRCQk5ESTFNV00wWXpZME9XTTNaREptT0RZek1qZGxabVJsTWpNNU9USm1ZVGNsTUVGaFlXVTNZakprTkRneU16Z3lZV0ZoWkRjMVptUmxOalJrWmpobVpqZzJaaVV3UVRJNU5tWTNabVpqTW1VME5UUTFaR00zTnpreU1EVXdZMlZpTkdFNE56RXhKVEJCTmpFd04yRmpNV0UxTldZeFpUQm1aV05pTjJSa1lqWXdabUl6WW1ZeE1Ea2xNRUZoWldNeU16TXpNekl4WkRjek1EQXdNVFl4TmpneVpETmpOR1ZpWXpBd09TVXdRVFV3TURWaU0ySm1NREF3TlRCaVpqUm1OMlUwTTJGak16TmhNRFExTkdJNEpUQkI=
It is not a very formal PEM format public key file. Try to tear it by hand, Base64 twice and URL once to get it
1b08af276dbc7593271f4ee616289324 e2ae3a2350743c516cda412499ba3be9 bde52cb31de33e46245e05fbdbd6fb24 e23e00be39d36f3462e576a67a7f9199 18c79285b514c63fc9035e3f920ae477 da44dd192defd1be79f63c350d2920cf 4251c4c649c7d2f86327efde23992fa7 aae7b2d482382aaad75fde64df8ff86f 296f7ffc2e4545dc7792050ceb4a8711 6107ac1a55f1e0fecb7ddb60fb3bf109 aec2333321d73000161682d3c4ebc009 5005b3bf00050bf4f7e43ac33a0454b8
It looks a bit like MTP. Run the script used by meituan and come up with such a thing. It doesn't have any practical meaning. It's numb
kGKû ¦¤B k 'áÞÿ9èYâZhd+Ј¦ ͪÈot[õìS»i¼Hk 'qäbPO ‡TW æÈ"Ö hˆvY܈£Œÿ `W8 ODju¿C"€ 2 [·KU•¹ž'óœè Ú¨ë¤Oáíˆ$måK Y › GÙ oA SLY 4^ HHÆ<m MýÏ IQBF Þ×ïHKU³ ¤Ô"vsF JWci™nGÁVlƒˆnç÷
Then I saw that wp is a hash function type, and then I found websites with reverse hash. Some websites have to log in and charge; Several successful discoveries are md4, and the results have numbers and letters, so write a blow up
I remember that there seems to be no md4 in the hashlib library, so I casually found a source code from github
def _pad(msg):
n = len(msg)
bit_len = n * 8
index = n & 0x3f
pad_len = 120 - index
if index < 56:
pad_len = 56 - index
padding = b'\x80' + b'\x00' * 63
suffix = bit_len.to_bytes(8, 'little', signed=False)
padded_msg = msg + padding[:pad_len] + suffix
return padded_msg
def _left_rotate(n, b):
return ((n << b) | ((n & 0xffffffff) >> (32 - b))) & 0xffffffff
def _if(x, y, z):
return x & y | ~x & z
def _maj(x, y, z):
return x & y | x & z | y & z
def _xor3(x, y, z):
return x ^ y ^ z
def _f1(a, b, c, d, k, s, X):
return _left_rotate(a + _if(b, c, d) + X[k], s)
def _f2(a, b, c, d, k, s, X):
return _left_rotate(a + _maj(b, c, d) + X[k] + 0x5a827999, s)
def _f3(a, b, c, d, k, s, X):
return _left_rotate(a + _xor3(b, c, d) + X[k] + 0x6ed9eba1, s)
class MD4:
def __init__(self):
self.A = 0x67452301
self.B = 0xefcdab89
self.C = 0x98badcfe
self.D = 0x10325476
def update(self, message_string):
msg_bytes = _pad(message_string)
for i in range(0, len(msg_bytes), 64):
self._compress(msg_bytes[i:i + 64])
def _compress(self, block):
a, b, c, d = self.A, self.B, self.C, self.D
x = []
for i in range(0, 64, 4):
x.append(int.from_bytes(block[i:i + 4], 'little', signed=False))
a = _f1(a, b, c, d, 0, 3, x)
d = _f1(d, a, b, c, 1, 7, x)
c = _f1(c, d, a, b, 2, 11, x)
b = _f1(b, c, d, a, 3, 19, x)
a = _f1(a, b, c, d, 4, 3, x)
d = _f1(d, a, b, c, 5, 7, x)
c = _f1(c, d, a, b, 6, 11, x)
b = _f1(b, c, d, a, 7, 19, x)
a = _f1(a, b, c, d, 8, 3, x)
d = _f1(d, a, b, c, 9, 7, x)
c = _f1(c, d, a, b, 10, 11, x)
b = _f1(b, c, d, a, 11, 19, x)
a = _f1(a, b, c, d, 12, 3, x)
d = _f1(d, a, b, c, 13, 7, x)
c = _f1(c, d, a, b, 14, 11, x)
b = _f1(b, c, d, a, 15, 19, x)
a = _f2(a, b, c, d, 0, 3, x)
d = _f2(d, a, b, c, 4, 5, x)
c = _f2(c, d, a, b, 8, 9, x)
b = _f2(b, c, d, a, 12, 13, x)
a = _f2(a, b, c, d, 1, 3, x)
d = _f2(d, a, b, c, 5, 5, x)
c = _f2(c, d, a, b, 9, 9, x)
b = _f2(b, c, d, a, 13, 13, x)
a = _f2(a, b, c, d, 2, 3, x)
d = _f2(d, a, b, c, 6, 5, x)
c = _f2(c, d, a, b, 10, 9, x)
b = _f2(b, c, d, a, 14, 13, x)
a = _f2(a, b, c, d, 3, 3, x)
d = _f2(d, a, b, c, 7, 5, x)
c = _f2(c, d, a, b, 11, 9, x)
b = _f2(b, c, d, a, 15, 13, x)
a = _f3(a, b, c, d, 0, 3, x)
d = _f3(d, a, b, c, 8, 9, x)
c = _f3(c, d, a, b, 4, 11, x)
b = _f3(b, c, d, a, 12, 15, x)
a = _f3(a, b, c, d, 2, 3, x)
d = _f3(d, a, b, c, 10, 9, x)
c = _f3(c, d, a, b, 6, 11, x)
b = _f3(b, c, d, a, 14, 15, x)
a = _f3(a, b, c, d, 1, 3, x)
d = _f3(d, a, b, c, 9, 9, x)
c = _f3(c, d, a, b, 5, 11, x)
b = _f3(b, c, d, a, 13, 15, x)
a = _f3(a, b, c, d, 3, 3, x)
d = _f3(d, a, b, c, 11, 9, x)
c = _f3(c, d, a, b, 7, 11, x)
b = _f3(b, c, d, a, 15, 15, x)
# update state
self.A = (self.A + a) & 0xffffffff
self.B = (self.B + b) & 0xffffffff
self.C = (self.C + c) & 0xffffffff
self.D = (self.D + d) & 0xffffffff
def digest(self):
return binascii.hexlify(
self.A.to_bytes(4, 'little', signed=False) + \
self.B.to_bytes(4, 'little', signed=False) + \
self.C.to_bytes(4, 'little', signed=False) + \
self.D.to_bytes(4, 'little', signed=False)
).decode('ascii')
EXP
from sage import MD4
from string import printable
cipher = '''1b08af276dbc7593271f4ee616289324
e2ae3a2350743c516cda412499ba3be9
bde52cb31de33e46245e05fbdbd6fb24
e23e00be39d36f3462e576a67a7f9199
18c79285b514c63fc9035e3f920ae477
da44dd192defd1be79f63c350d2920cf
4251c4c649c7d2f86327efde23992fa7
aae7b2d482382aaad75fde64df8ff86f
296f7ffc2e4545dc7792050ceb4a8711
6107ac1a55f1e0fecb7ddb60fb3bf109
aec2333321d73000161682d3c4ebc009
5005b3bf00050bf4f7e43ac33a0454b8'''
for i in printable:
m = MD4()
m.update(i.encode('ascii'))
t = m.digest()
if t in cipher:
cipher = cipher.replace(t, i)
for i in cipher.split():
print(i, end='')
Get flag
flag{36D_me}
There is no need to worry about md4 in the future. In addition, md4 is also 32-bit
BJDCTF
Coding and modulation
Title Description
Ciphertext: 2559659965656 A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6
hint
Problem solving ideas
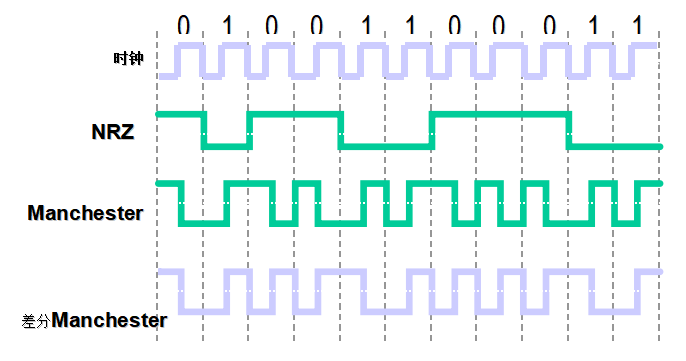
Network knowledge, Manchester and differential Manchester
- Standard Manchester: low to high 0, high to 1
- IEEE Manchester: just the opposite, low to high 1, high to 0
- Difference Manchester: the same before and after is 0, and the difference is 1
- Other types: only 5, 6, 9, a
- Note: there is a problem of byte reverse order: every 8 bytes are in reverse order
I saw in la guy's blog long ago that the script encoded by Manchester is finally used this time. Put it away
Obviously, there are only 569a characters in the ciphertext, which can be found here in other solutions

The first one is omitted here. Other variants are not excluded. Back up the script
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import struct
import math
def long_to_bytes(n):
s = b''
pack = struct.pack
while n > 0:
s = pack('>I', n & 0xffffffff) + s
n = n >> 32
for i in range(len(s)):
if s[i] != b'\000'[0]:
break
else:
s = b'\000'
i = 0
s = s[i:]
return s
# Byte reverse order
def byteinvert(str_bin):
ret = ''
for i in range(len(str_bin) // 8):
ret += str_bin[i * 8:i * 8 + 8][::-1]
return ret
# Standard Manchester
def MCST_stand(str_bin):
ret = ''
for i in range(len(str_bin) // 2):
x = str_bin[i * 2:i * 2 + 2]
if x == '01':
ret += '0'
elif x == '10':
ret += '1'
else:
return 'stand manchester decode wrong!'
return ret
# Manchester in IEEE
def MCST_IEEE(str_bin):
ret = ''
for i in range(math.ceil(len(str_bin) / 8)):
x = str_bin[i * 2:i * 2 + 2]
if x == '01':
ret += '1'
elif x == '10':
ret += '0'
else:
return 'stand manchester decode wrong!'
return ret
# Differential Manchester
def MCST_diff(str_bin):
ret = ''
for i in range(0, len(str_bin) // 2 - 1):
x1 = str_bin[i * 2:i * 2 + 2]
x2 = str_bin[i * 2 + 2:i * 2 + 4]
if x1 == x2:
ret += '0'
else:
ret += '1'
return ret
if __name__ == "__main__":
str_hex = '2559659965656A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6'
# str_bin='0101010101010101'
str_bin = str(bin(int(str_hex, 16)))[2:]
m1 = MCST_IEEE(str_bin)
m2 = MCST_stand(str_bin)
m3 = MCST_diff(str_bin)
print('\nIEEE Manchester:')
print(m1)
print(hex(int(m1, 2)))
print(long_to_bytes(int(m1, 2)))
print('\n Standard Manchester:')
print(m2)
print(hex(int(m2, 2)))
print(long_to_bytes(int(m2, 2)))
print('\n Differential Manchester:')
print(m3)
print(hex(int(m3, 2)))
print(long_to_bytes(int(m3, 2)))
print('\n=============Byte reverse order=============')
m1 = byteinvert(m1)
m2 = byteinvert(m2)
m3 = byteinvert(m3)
print('\nIEEE Manchester:')
print(m1)
print(hex(int(m1, 2)))
print(long_to_bytes(int(m1, 2)))
print('\n Standard Manchester:')
print(m2)
print(hex(int(m2, 2)))
print(long_to_bytes(int(m2, 2)))
print('\n Differential Manchester:')
print(m3)
print(hex(int(m3, 2)))
print(long_to_bytes(int(m3, 2)))
Polybius
Ciphertext: ouauuuoooeeaaiaeauieuooeeiea hint: VGhlIGxlbmd0aCBvZiB0aGlzIHBsYWludGV4dDogMTQ=
hint solution
The length of this plaintext: 14
The ciphertext is all composed of five vowels. The length of the plaintext is half of the ciphertext. The title prompt is the polibios chessboard password, without saying the key
The so-called polibios chessboard password belongs to the same chessboard password as playfair. It uses the coordinates of the character table instead of sitting; Therefore, there are only 1-5. Like playfair, i is used instead of j by default; There are no special instructions here. This is the key
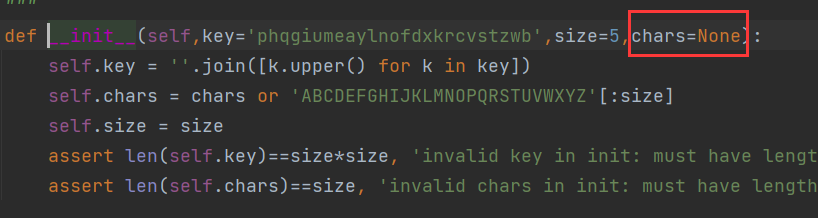
First turn it into a number. Here I was confused for the first time, because it is not necessarily in the order of aeiou, but also needs to be blasted, which means that there are 120 possibilities; An off the shelf python library implementation was found
After reading it, I can understand that there is a pit, which makes me correct it by directly debugging the code in the library. That is, this parameter must be capitalized, otherwise an error will be reported later because it cannot be found
EXP
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from itertools import permutations
from pycipher import PolybiusSquare
from string import ascii_lowercase
square = ascii_lowercase.replace('j', '')
space = 'AEIOU'
cipher = 'ouauuuoooeeaaiaeauieuooeeiea'
for i in permutations(space, 5):
l = ''.join(list(i))
p = PolybiusSquare(key=square, size=5, chars=l)
m = p.decipher(cipher).lower()
if m.startswith('flag'):
print(m)
Good guy, I found the treasure
Cryptography AK competition
addition
vtu[ypslg;sh}lrunpstf[sddeptf\
I'm familiar with it, but I can't tell what encryption is; I was going to give up, then randomly extract a paragraph and search it. I found a CSDN blog that talked about moving the password key to the right one bit in order to make the password safe. The so-called key position is the position on the keyboard
Direct hand tear
cryptoakflag{keyboardpassword}
No, let's stop here first. I glanced at Jiang Shao's ranking. It's so bad. Is the gap so big