I went to the north to support teaching in the past two weeks. When I came back, I went to the Red Hat Cup. Ha ha, I ran half of China and gained a lot. But the Red Hat Cup's zero contribution once again made me know the necessity of learning pwn. Return and start training. You can settle down
The tail game in July has not been completely reproduced. It starts first in one breath, and then there is a game
2021DASCTF actual combat elite summer camp and DASCTF July X CBCTF 4th
Crypto yusa's cryptography sign in -- BlockTrick
from Crypto.Cipher import AES
import os
def pad(a):
size = (16-len(a)%16)%16
a += chr(size)*size
return a
iv = os.urandom(16)
key = os.urandom(16)
enc = AES.new(key,AES.MODE_CBC,iv)
print(iv.encode('hex'))
for _ in range(2):
try:
trick = raw_input("")
trick = pad(trick.decode('hex'))
cipher = enc.encrypt(trick)
if trick == cipher and trick != "":
with open("flag.txt") as f:
print(f.read())
exit()
else:
print(cipher.encode('hex'))
print("Try again")
except:
exit()
The idea given by master Shang, two rounds of AES_CBC, use known IV to XOR. The specific process is still to look at the CBC process. It's difficult to think about it, but it's difficult to think through it
# !/usr/bin/env python
# -*- coding:utf-8 -*-
from pwn import *
context.log_level = 'debug'
sh = remote('node4.buuoj.cn', 25321)
iv = sh.recv()
# first time
sh.send(iv)
cipher = sh.recvline()
sh.recv()
# second time
sh.send(cipher)
sh.recv()
Crypto yusa's cryptography class - SEDSED (recycling)
import os
from My_box import *
def gen_key(key):
key_64 = ""
for i in range(16):
key_64 += '{0:04b}'.format(int(key[i], 16))
key_56 = gen_56bit(key_64)
left_key, right_key = key_56[:28], key_56[28:]
round_keys = list()
for index in range(2):
L = circular_shift(left_key, round_shifts[index])
R = circular_shift(right_key, round_shifts[index])
round_key = gen_48bit(L + R)
round_keys.append(round_key)
left_key = L
right_key = R
return round_keys
def circular_shift(key, n):
temp = ""
temp = key[n:] + key[:n]
return temp
def gen_56bit(key):
key_56 = ""
for x in KEY_P1:
key_56 += key[x - 1]
return key_56
def gen_48bit(key):
key_48 = ""
for x in KEY_P2:
key_48 += key[x - 1]
return key_48
def encrypt(plain_text, sub_keys):
plain_textb = ""
for i in range(16):
plain_textb += '{0:04b}'.format(int(plain_text[i], 16))
plain_textp = permutation(plain_textb)
left, right = plain_textp[:32], plain_textp[32:]
out = func(right, sub_keys[0])
temp = int(out, 2) ^ int(left, 2)
left, right = right, '{0:032b}'.format(temp)
out = func(right, sub_keys[1])
temp = int(out, 2) ^ int(left, 2)
left = '{0:032b}'.format(temp)
final = inv_permutation(left + right)
cipher = hex(int(final, 2))[2:]
return cipher
def permutation(plain_text):
p = ""
for x in IP:
p += plain_text[x - 1]
return p
def func(text, key):
exp = expand(text)
s_input = '{0:048b}'.format(int(exp, 2) ^ int(key, 2))
s_out = sbox(s_input)
f_final = per_func(s_out)
return f_final
def expand(text):
temp = ""
for x in E:
temp += text[x - 1]
return temp
def inv_permutation(text):
final = ""
for x in Inv_IP:
final += text[x - 1]
return final
def per_func(s_output):
s_final = ""
for x in P:
s_final += s_output[x - 1]
return s_final
def sbox(s_input, index=None):
s_out = ""
if index != None:
i = index
row = int(s_input[0] + s_input[5], 2)
column = int(s_input[1:5], 2)
s_out += '{0:04b}'.format(S[i][row][column])
return s_out
else:
for i in range(8):
row = int(s_input[6 * i] + s_input[6 * i + 5], 2)
column = int(s_input[6 * i + 1:6 * i + 5], 2)
s_out += '{0:04b}'.format(S[i][row][column])
return s_out
def enc(plain_text):
sub_keys = gen_key(key_64)
cipher_text = encrypt(plain_text, sub_keys)
return cipher_text
def pad(plain_text):
size = (16 - (len(plain_text) % 16)) % 16
plain_text += size * '0'
return plain_text
def myenc(plain_text):
plain_text = pad(plain_text)
cipher_text = ""
for i in range(0, len(plain_text), 16):
block = plain_text[i:i + 16]
block_enc = enc(block).rjust(16, '0')
cipher_text += block_enc
return cipher_text
def enc2(plain_text, key):
sub_keys = gen_key(key)
cipher_text = encrypt(plain_text, sub_keys)
return cipher_text
key_64 = os.urandom(8).hex()
teststring = "testtest"
print(enc2(teststring.encode().hex(), key_64))
with open("flag.txt") as f:
flag = f.read()
print("flag: ", myenc(flag.encode().hex()))
# 77a35598c47aeea6
# flag: 86721c7c1ebe2d0af8aa8e073073931b4a5ae6dcf03c784e3c70b5f8ce71cf9eb87f9b836eea0118
My_box
# 64->56
KEY_P1 = [57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18, 10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22, 14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4]
round_shifts = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
# 56->48
KEY_P2 = [14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10, 23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2, 41, 52, 31, 37, 47,
55, 30, 40, 51, 45, 33, 48, 44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32]
IP = [58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4, 62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32,
24, 16, 8, 57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3, 61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47,
39, 31, 23, 15, 7]
E = [32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17, 16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1]
S = [
# Box-1
[
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
],
# Box-2
[
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
],
# Box-3
[
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]
],
# Box-4
[
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]
],
# Box-5
[
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
],
# Box-6
[
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]
],
# Box-7
[
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
],
# Box-8
[
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
]
]
P = [16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10, 2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4,
25]
Inv_P = [9, 17, 23, 31, 13, 28, 2, 18, 24, 16, 30, 6, 26, 20, 10, 1, 8, 14, 25, 3, 4, 29, 11, 19, 32, 12, 22, 7, 5, 27,
15, 21]
Inv_IP = [40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31, 38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13,
53, 21, 61, 29, 36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27, 34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
def inverse_table(table):
new = list()
for x in range(len(table)):
if (x + 1) in table:
num = table.index(x + 1) + 1
new.append(num)
else:
new.append(x)
return new
After listening to the V God, I still didn't understand it, but I saw that master Shang had made it, ignited it and reappeared his fighting spirit
I was ashamed to shrink up. Although I studied feistel and DES a little after the game, I was still ignored_ 64 += '{0:04b}'. The sentence format (int (key [i], 16)) discouraged me because I couldn't understand {0:04b} and felt it was so complicated; It's still very inappropriate. I really don't understand. Look at your output during the game
After checking, it is expressed in 4-bit binary, and 4-bit binary is enough for 1-bit hexadecimal
So learn from the bitter experience. Since I don't understand it, I try to reproduce the whole des process. Red indicates the known and directly pushable parts, and green indicates the places that need to be blasted. Now it's clear
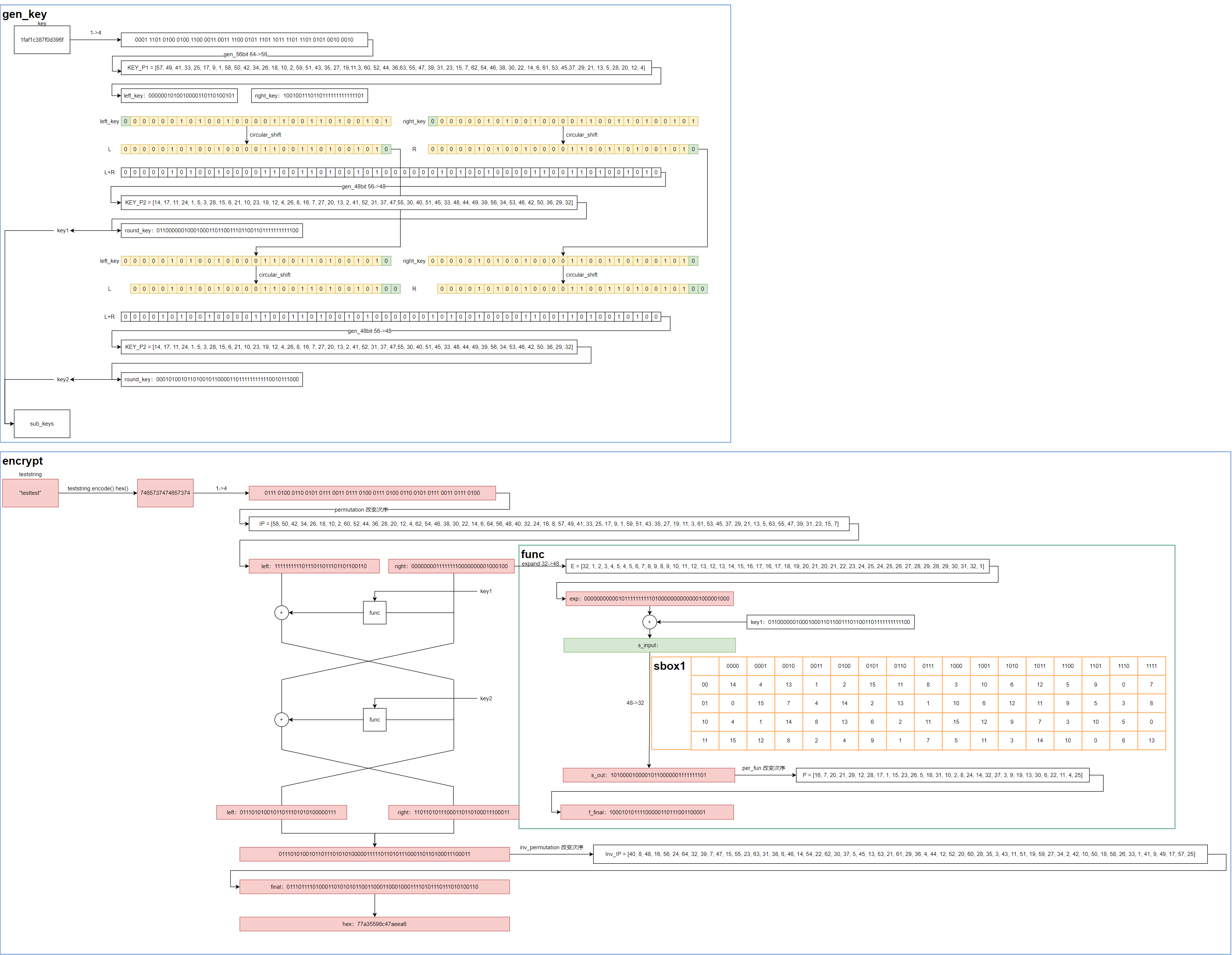
svg diagram is not supported, paste one link , masters who are interested in guidance can open the link in the browser and download it. (finally, I found that it is not necessary to draw in such detail. It is almost enough to know a func; but after all, I didn't understand it before. Detour is the shortest shortcut for me.)
The idea of the whole problem is to encrypt the known testtest with a group of random keys to get the result 77a35598c47aeea6, and encrypt our flag with the same key; Then the idea of solving the problem is also very clear. Try to get the key through the known ciphertext, then write the decryption function, and finally return to
Start with key1 (I wrote key1 casually in the figure), and just focus on the feistel structure above
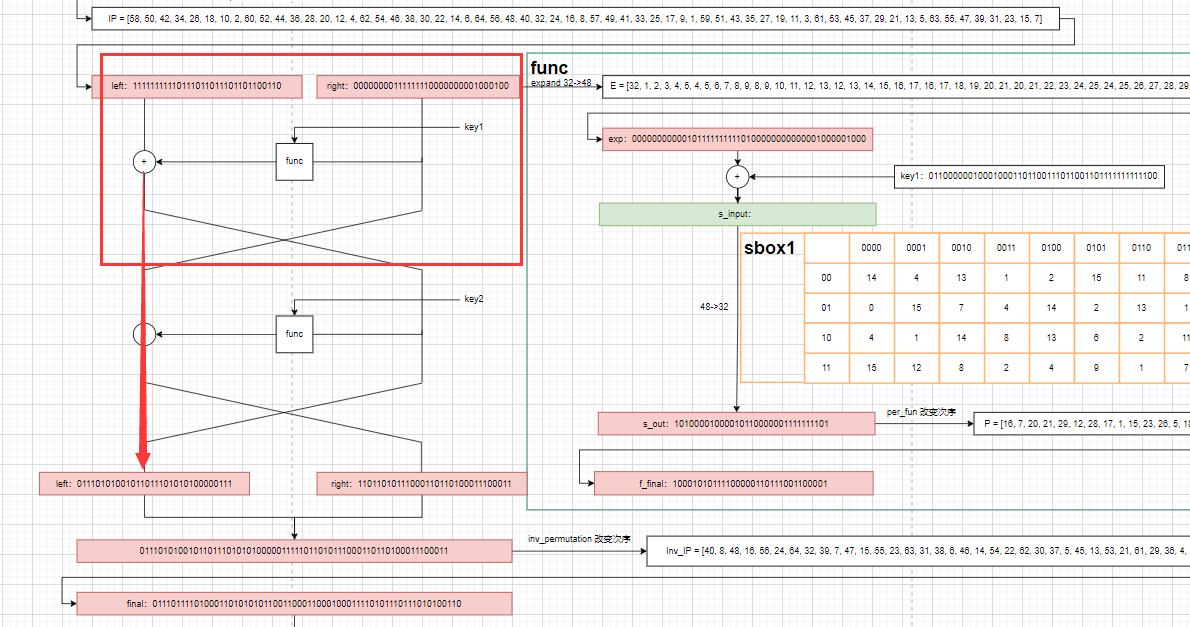
Some parts can be directly reversed, such as inv_permutation and per_func these two functions can be reversed in this way. It's a little smelly
def inv_permutation(text):
final = ""
for x in Inv_IP:
final += text[x - 1]
return final
def per_func(s_output):
s_final = ""
for x in P:
s_final += s_output[x - 1]
return s_final
null = ['' for _ in range(64)]
def permutation(plain_text):
assert len(plain_text) == len(Inv_IP)
final = null
for x in range(len(Inv_IP)):
final[Inv_IP[x]-1] = plain_text[x]
return ''.join(final)
Then the key to this topic is to explode this sbox; The working principle of sbox is simply to convert 48 bits to 32 bits, and the middle is to convert 8 bits every 6 bits. For example, in the wiki encyclopedia, taking sbox 5 as an example, the beginning and end of 011011 is 01, and the middle is 1101, that is, the corresponding coordinates 1,13, The corresponding sandbox (which can be checked in the table) is 1001. After this operation, the original 48 bit sandbox is divided into 8 groups, and each group of 6 bits becomes 4 bits, so the final total length is 32. Obviously, this process is irreversible

Carefully observe the sandbox and find that the 16 numbers 0 ~ 15 in a row are out of order, so a sandbox needs to be exploded in four cases
I wrote the script, but I felt that my code ability was really poor. Variable naming became a problem. Finally, I couldn't check out any errors. I'll make up later
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from My_box import *
import sys
from Crypto.Util.number import long_to_bytes
teststring = "testtest"
cipher = 0x77a35598c47aeea6
final = bin(cipher)[2:].rjust(64, '0')
c = '86721c7c1ebe2d0af8aa8e073073931b4a5ae6dcf03c784e3c70b5f8ce71cf9eb87f9b836eea0118'
null64 = ['' for _ in range(64)]
null32 = ['' for _ in range(32)]
def my_permutation(plain_text):
assert len(plain_text) == len(Inv_IP)
per_final = null64
for x in range(len(Inv_IP)):
per_final[Inv_IP[x]-1] = plain_text[x]
return ''.join(per_final)
def expand(text):
temp = ""
for x in E:
temp += text[x - 1]
return temp
def inv_per_func(s_final):
assert len(s_final) == len(P)
s_output = null32
for x in range(len(P)):
s_output[P[x] - 1] = s_final[x]
return ''.join(s_output)
def func(text):
exp = expand(text)
return exp
def find_column(num, index, row):
for find_j in range(16):
if S[index][row][find_j] == num:
return find_j
def permutation(plain_text):
p = ""
for x in IP:
p += plain_text[x - 1]
return p
def encrypt(plain_text):
plain_textb = ""
for en_i in range(16):
plain_textb += '{0:04b}'.format(int(plain_text[en_i], 16))
plain_textp = permutation(plain_textb)
en_left, en_right = plain_textp[:32], plain_textp[32:]
out = func(en_right)
return en_left, en_right, out
def sbox(s_input):
s_out = ''
for sbox_i in range(8):
s_row = int(s_input[6 * sbox_i] + s_input[6 * sbox_i + 5], 2)
s_column = int(s_input[6 * sbox_i + 1:6 * sbox_i + 5], 2)
s_out += '{0:04b}'.format(S[sbox_i][s_row][s_column])
return s_out
def per_func(s_output):
s_final = ""
for x in P:
s_final += s_output[x - 1]
return s_final
def inv_permutation(cipher_text):
assert len(cipher_text) == len(IP)
p = null64
for x in range(len(IP)):
p[IP[x] - 1] = cipher_text[x]
return ''.join(p)
def decrypt(cipher_text, d_sub_keys):
d_final = bin(int(cipher_text, 16))[2:].rjust(64, '0')
d_final = my_permutation(d_final)
d_left, d_right = d_final[:32], d_final[32:]
# RIGHT
d_EXP = func(d_left)
# inv_func
d_s_input = '{0:048b}'.format(int(d_EXP, 2) ^ int(d_sub_keys[1], 2))
d_s_out = sbox(d_s_input)
out = per_func(d_s_out)
d_RIGHT = bin(int(out, 2) ^ int(d_right, 2))[2:].rjust(32, '0')
# LEFT
d_EXP = func(d_RIGHT)
d_s_input = '{0:048b}'.format(int(d_EXP, 2) ^ int(d_sub_keys[0], 2))
d_s_out = sbox(d_s_input)
out = per_func(d_s_out)
d_LEFT = bin(int(out, 2) ^ int(d_left, 2))[2:].rjust(32, '0')
plaintext = d_LEFT + d_RIGHT
plaintext = inv_permutation(plaintext)
plaintext = ''.join(hex(int(plaintext[_:_+4], 2))[2:] for _ in range(0, len(plaintext), 4))
return plaintext
def inv_rjust(cipher_text):
for rjust_i in range(len(cipher_text)):
if cipher_text[rjust_i] != '0':
return cipher_text[rjust_i:]
def inv_pad(cipher_text):
for pad_i in range(len(cipher_text)-1, -1, -1):
if cipher_text[pad_i] != '0':
return cipher_text[:pad_i]
def mydec(ciphertext, d_sub_keys):
plaintext = ''
for de_i in range(0, len(ciphertext), 16):
block_enc = inv_rjust(ciphertext[de_i:de_i + 16])
block = decrypt(block_enc, d_sub_keys)
plaintext += block
plaintext = inv_pad(plaintext)
return plaintext
LEFT, RIGHT, EXP1 = encrypt(teststring.encode().hex())
final = my_permutation(final)
left, right = final[:32], final[32:]
EXP2 = func(left)
# key1
f_final1 = bin(int(left, 2) ^ int(LEFT, 2))[2:].rjust(32, '0')
# inv_func
s_out1 = inv_per_func(f_final1)
# inv_sbox
for i in range(65536):
bin_i = bin(i)[2:].rjust(16, '0')
a1 = [int(bin_i[_]+bin_i[_+1], 2) for _ in range(0, len(bin_i), 2)]
# j's sbox
j1 = 0
# i's row
s_input1 = ''
for i1 in a1:
t1 = int(s_out1[i1 * 4:i1 * 4 + 4], 2)
column1 = find_column(t1, j1, i1)
j1 += 1
s_input1 += bin(i1)[2:].rjust(2, '0')[0] + bin(column1)[2:].rjust(4, '0') + bin(i1)[2:].rjust(2, '0')[-1]
key1 = bin(int(s_input1, 2) ^ int(EXP1, 2))[2:].rjust(48, '0')
# key2
f_final2 = bin(int(right, 2) ^ int(RIGHT, 2))[2:].rjust(32, '0')
s_out2 = inv_per_func(f_final2)
for j in range(65536):
bin_j = bin(j)[2:].rjust(16, '0')
a2 = [int(bin_j[_] + bin_j[_ + 1], 2) for _ in range(0, len(bin_j), 2)]
j2 = 0
s_input2 = ''
for i2 in a2:
t2 = int(s_out2[j2 * 4:j2 * 4 + 4], 2)
column2 = find_column(t2, j2, i2)
j2 += 1
s_input2 += bin(i2)[2:].rjust(2, '0')[0] + bin(column2)[2:].rjust(4, '0') + bin(i2)[2:].rjust(2, '0')[-1]
key2 = bin(int(s_input2, 2) ^ int(EXP2, 2))[2:].rjust(48, '0')
sub_keys = [key1, key2]
flag = long_to_bytes(int(mydec(c, sub_keys), 16))
print(i, i*j)
if b'flag' in flag:
print(flag)
sys.exit(0)
Misc-red_vs_blue
Classic red blue duel, Misc's sign in question, but to be honest, I'm a little numb
Given an nc, you can know that there are two situations for you to guess. You can get the flag 66 times in a row. Each time you win or lose an nc, the results are different
This was my script at that time. I thought there was no problem, but the interaction made me hemoptysis several times and all kinds of IO confusion
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from pwn import *
def rest():
# not so fast
time.sleep(.05)
context.log_level = 'debug'
res = []
r = b'r'
b = b'b'
sh = remote('node4.buuoj.cn', 28719)
# begin info
sh.recv()
while 1:
# classical try red one
rest()
bug = sh.sendline(r)
feedback = sh.recv()
if b'Sorry' in feedback:
res.append(b)
sh.sendline(b'y')
else:
res.append(r)
continue
sh.recv()
for i in res:
rest()
sh.sendline(i)
flag = sh.recv()
if b'flag' in flag:
print(flag)
sh.close()
break
print(len(res))
Then I asked pwn how to achieve good interaction effect; Finally, President Peng gave a script, learned it, wrote it well and neatly, and set a good example for our generation. Post it and learn again in the future
Mainly some format conversion, and then receive it sentence by sentence
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from pwn import *
# connection
p = remote('node4.buuoj.cn', 28719)
# receive intro text
p.recvline() # Here are 66 AWD Games will begin!
p.recvline() # The winner is between Red Team and Blue Team
p.recvline() # To get the flag if you predict the results of all games successfully!
p.recvline() # Game 1
p.recvline() # choose one [r] Red Team,[b] Blue Team:
# record the results
s = ''
while 1:
p.sendline(bytes("r", encoding="utf-8"))
print("r")
print(p.recvline().decode(), end="") # Your choice xxx Team
print(p.recvline().decode(), end="") # The result xxx Team
# win: The number of successful predictions xx
# lose: Sorry!You are wrong!
result = p.recvline().decode()
print(result)
# print(result.find("successful"))
if result.find("successful") != -1:
# print("continue..")
s += "r"
print(p.recvline().decode(), end="") # Game x
p.recvline() # choose one [r] Red Team,[b] Blue Team:
elif result.find("wrong") != -1:
# print("retry..")
s += "b"
p.sendline(bytes("y", encoding="utf-8"))
print(p.recvline().decode(), end="") # Play again? (y/n):Game 1
print("y")
# repeat
for i in range(len(s)):
# print(p.recvline().decode(),end="")# Game x
p.recvline()
# print(p.recvline().decode(),end="")# choose one [r] Red Team,[b] Blue Team:
p.sendline(bytes(s[i], encoding="utf-8"))
print(s[i])
p.recvline() # Your choice xxx Team
p.recvline() # The result xxx Team
p.recvline() # win: The number of successful predictions xx
print(p.recvline().decode(), end="") # Game x
print(p.recvline().decode(), end="") # choose one [r] Red Team,[b] Blue Team:
Geek peak
Crypto-crtrsa
from secret import flagn,p,q #p and q are two primes generated by getPrime import random def key_gen(): while True: dp = random.randint(1,1<<20) dq = random.randint(1,q-1) if gcd(dp, p - 1) == 1 and gcd(dq, q - 1) == 1: d = crt([dp,dq],[p-1,q-1]) phi = (p-1)*(q-1) R = Integers(phi) e = R(d)^-1 return p*q,e n,e = key_gen() print(e) print(n) print(pow(flagn,int(e),n))
e = 2953544268002866703872076551930953722572317122777861299293407053391808199220655289235983088986372630141821049118015752017412642148934113723174855236142887 N = 6006128121276172470274143101473619963750725942458450119252491144009018469845917986523007748831362674341219814935241703026024431390531323127620970750816983 flag = 4082777468662493175049853412968913980472986215497247773911290709560282223053863513029985115855416847643274608394467813391117463817805000754191093158289399
E is big, but obviously d is also big, so neither of those guys can; From the known point of view, it looks like dp leakage, but e is too large to enumerate; Finally see A Master Blog RSA - Small CRT Private Exponents are recorded on the. Unfortunately, the master didn't give exp; Then I also found relevant papers, which were all over the street, but I couldn't understand them; Then I found the implementation on github, which is a tool small from the RsaCtfTool of password dog hand_ crt_ Exp, post the link https://github.com/Ganapati/RsaCtfTool , but I didn't quite understand how to use the command line. I took the source code directly and pieced it together. The complete exp is
# sage
from sage.libs.ntl.ntl_ZZ_pX import ntl_ZZ_pContext, ntl_ZZ_pX
from functools import reduce
import binascii
import math
import logging
import random
logger = logging.getLogger("global_logger")
try:
import gmpy2 as gmpy
gmpy_version = 2
mpz = gmpy.mpz
logger.info("[+] Using gmpy version 2 for math.")
except ImportError:
try:
import gmpy
gmpy_version = 1
mpz = gmpy.mpz
logger.info("[+] Using gmpy version 1 for math.")
except ImportError:
gmpy_version = 0
mpz = int
gmpy = None
logger.info("[+] Using python native functions for math.")
def getpubkeysz(n):
size = int(math.log2(n))
if size & 1 != 0:
size += 1
return size
def _gcdext(a, b):
if a == 0:
return [b, 0, 1]
else:
d = b // a
r = b - (d * a)
g, y, x = _gcdext(r, a)
return [g, x - d * y, y]
def _isqrt(n):
if n == 0:
return 0
x, y = n, (n + 1) >> 1
while y < x:
x, y = y, (y + n // y) >> 1
return x
def _gcd(a, b):
while b:
a, b = b, a % b
return abs(a)
def _introot(n, r=2):
if n < 0:
return None if r & 1 == 0 else -_introot(-n, r)
if n < 2:
return n
if r == 2:
return _isqrt(n)
lower, upper = 0, n
while lower != upper - 1:
mid = (lower + upper) >> 1
m = pow(mid, r)
if m == n:
return mid
elif m < n:
lower = mid
elif m > n:
upper = mid
return lower
def _introot_gmpy(n, r=2):
if n < 0:
return None if r & 1 == 0 else -_introot_gmpy(-n, r)
return gmpy.root(n, r)[0]
def _introot_gmpy2(n, r=2):
if n < 0:
return None if r & 1 == 0 else -_introot_gmpy2(-n, r)
return gmpy.iroot(n, r)[0]
def _invmod(a, m):
a, x, u = a % m, 0, 1
while a:
x, u, m, a = u, x - (m // a) * u, a, m % a
return x
def _is_square(n):
i = _isqrt(n)
return i ** 2 == n
def miller_rabin(n, k=40):
# Taken from https://gist.github.com/Ayrx/5884790
# Implementation uses the Miller-Rabin Primality Test
# The optimal number of rounds for this test is 40
# See http://stackoverflow.com/questions/6325576/how-many-iterations-of-rabin-miller-should-i-use-for-cryptographic-safe-primes
# for justification
# If number is even, it's a composite number
if n == 2:
return True
if n & 1 == 0:
return False
r, s = 0, n - 1
while s & 1 == 0:
r += 1
s >>= 1
i = 0
for i in range(0, k):
a = random.randrange(2, n - 1)
x = pow(a, s, n)
if x == 1 or x == n - 1:
continue
j = 0
while j <= r - 1:
x = pow(x, 2, n)
if x == n - 1:
break
j += 1
else:
return False
return True
def _fermat_prime_criterion(n, b=2):
"""Fermat's prime criterion
Returns False if n is definitely composite, True if posible prime."""
return pow(b, n - 1, n) == 1
def _is_prime(n):
"""
If fermats prime criterion is false by short circuit we dont need to keep testing bases, so we return false for a guaranteed composite.
Otherwise we keep trying with primes 3 and 5 as base. The sweet spot is primes 2,3,5, it doesn't improvee the runing time adding more primes to test as base.
If all the previus tests pass then we try with rabin miller.
All the tests are probabilistic.
"""
if (
_fermat_prime_criterion(n)
and _fermat_prime_criterion(n, b=3)
and _fermat_prime_criterion(n, b=5)
):
return miller_rabin(n)
else:
return False
def _next_prime(n):
while True:
if _is_prime(n):
return n
n += 1
def erathostenes_sieve(n):
""" Returns a list of primes < n """
sieve = [True] * n
for i in range(3, isqrt(n) + 1, 2):
if sieve[i]:
sieve[pow(i, 2) :: (i << 1)] = [False] * (
(n - pow(i, 2) - 1) // (i << 1) + 1
)
return [2] + [i for i in range(3, n, 2) if sieve[i]]
_primes = erathostenes_sieve
def _primes_yield(n):
p = i = 1
while i <= n:
p = next_prime(p)
yield p
i += 1
def _primes_yield_gmpy(n):
p = i = 1
while i <= n:
p = gmpy.next_prime(p)
yield p
i += 1
def _primes_gmpy(n):
return list(_primes_yield_gmpy(n))
def _fib(n):
a, b = 0, 1
i = 0
while i <= n:
a, b = b, a + b
i += 1
return a
def _invert(a, b):
return pow(a, b - 2, b)
def _lcm(x, y):
return (x * y) // _gcd(x, y)
def _ilog2_gmpy(n):
return int(gmpy.log2(n))
def _ilog_gmpy(n):
return int(gmpy.log(n))
def _ilog2_math(n):
return int(math.log2(n))
def _ilog_math(n):
return int(math.log(n))
def _ilog10_math(n):
return int(math.log10(n))
def _ilog10_gmpy(n):
return int(gmpy.log10(n))
def _mod(a, b):
return a % b
if gmpy_version > 0:
gcd = gmpy.gcd
invmod = gmpy.invert
gcdext = gmpy.gcdext
is_square = gmpy.is_square
next_prime = gmpy.next_prime
is_prime = gmpy.is_prime
fib = gmpy.fib
primes = _primes_gmpy
lcm = gmpy.lcm
invert = gmpy.invert
powmod = gmpy.powmod
ilog = _ilog_gmpy
ilog2 = _ilog2_gmpy
mod = gmpy.f_mod
log = gmpy.log
log2 = gmpy.log2
log10 = gmpy.log10
ilog10 = _ilog10_gmpy
if gmpy_version == 2:
isqrt = gmpy.isqrt
introot = _introot_gmpy2
else:
isqrt = gmpy.sqrt
introot = _introot_gmpy
else:
gcd = _gcd
isqrt = _isqrt
introot = _introot
invmod = _invmod
gcdext = _gcdext
is_square = _is_square
next_prime = _next_prime
fib = _fib
primes = erathostenes_sieve
is_prime = _is_prime
fib = _fib
primes = _primes
lcm = _lcm
invert = _invmod
powmod = pow
ilog = _ilog_math
ilog2 = _ilog2_math
mod = _mod
log = math.log
log2 = math.log2
log10 = math.log10
ilog10 = _ilog10_math
def trivial_factorization_with_n_phi(N, phi):
m = N - phi + 1
i = isqrt(pow(m, 2) - (N << 2)) # same as isqrt((m**2) - (4*n))
roots = int((m - i) >> 1), int((m + i) >> 1)
if roots[0] * roots[1] == N:
return roots
__all__ = [
getpubkeysz,
gcd,
isqrt,
introot,
invmod,
gcdext,
is_square,
next_prime,
is_prime,
fib,
primes,
lcm,
invert,
powmod,
ilog2,
ilog,
ilog10,
mod,
log,
log2,
log10,
trivial_factorization_with_n_phi,
]
def poly_fast_ntl(ctx, f, xs):
# Fast multipoint evaulation from Modern Computer Algebra 3rd edition 10.1
n = len(xs)
rems = [0] * (4 * n) # segment tree max size
def build_tree(i, l, r):
if l + 1 == r:
x = xs[l] if l < len(xs) else 0
rems[i] = ntl_ZZ_pX([-x, 1], ctx)
return
mid = (l + r) >> 1
build_tree(i * 2, l, mid)
build_tree(i * 2 + 1, mid, r)
rems[i] = rems[i * 2] * rems[i * 2 + 1]
build_tree(1, 0, n)
def compute(f, i, l, r):
if l + 1 == r:
yield f % rems[i]
return
mid = (l + r) >> 1
yield from compute(f % rems[2 * i], 2 * i, l, mid)
yield from compute(f % rems[2 * i + 1], 2 * i + 1, mid, r)
return map(lambda r: Integer(r.list()[0]), compute(f, 1, 0, n))
def factor(n, e, bound):
# https://mathoverflow.net/questions/120160/attack-on-crt-rsa
D = ceil(sqrt(bound))
ctx = ntl_ZZ_pContext(n) # NTL's polynomial multiplication is much faster
x = randint(1, n - 1)
xe = int(powmod(x, e, n))
poly_factors = []
for a in range(0, D):
poly_factors.append(ntl_ZZ_pX([-x, power_mod(xe, a, n)], ctx))
poly = product(poly_factors)
xed = int(powmod(xe, D, n))
ys = [int(powmod(xed, b, n)) for b in range(0, D)]
for t in poly_fast_ntl(ctx, poly, ys):
p = gcd(t, n)
if p > 1 and p < n:
return p, n // p
if __name__ == "__main__":
n = 6006128121276172470274143101473619963750725942458450119252491144009018469845917986523007748831362674341219814935241703026024431390531323127620970750816983
e = 2953544268002866703872076551930953722572317122777861299293407053391808199220655289235983088986372630141821049118015752017412642148934113723174855236142887
bound = 2**20 # upper bound of min(d_p, d_q)
for _ in range(3): # Retrying
r = factor(n, e, bound)
if r is not None:
p, q = r
print(p)
exit()
print(0) # Prints 0 if failed
This can be used to decompose p, which will not be repeated later; The routine of doing password problems is to know and find the source code
The cipher master from the destiny team directly deduced it. Starting from dp, which can be exploded, he obtained p, strong. Stick down Destiny team link
Crypto-MedicalImage(recuring)
from PIL import Image
from decimal import *
import numpy as np
import random
getcontext().prec = 20
def f1(x):
# It is based on logistic map in chaotic systems
# The parameter r takes the largest legal value
assert(x>=0)
assert(x<=1)
...
def f2(x):
# same as f1
...
def f3(x):
# same as f1
...
def encryptImage(path):
im = Image.open(path)
size = im.size
pic = np.array(im)
im.close()
r1 = Decimal('0.478706063089473894123')
r2 = Decimal('0.613494245341234672318')
r3 = Decimal('0.946365754637812381837')
w,h = size
for i in range(200):
r1 = f1(r1)
r2 = f2(r2)
r3 = f3(r3)
const = 10**14
for x in range(w):
for y in range(h):
x1 = int(round(const*r1))%w
y1 = int(round(const*r2))%h
r1 = f1(r1)
r2 = f2(r2)
tmp = pic[y,x]
pic[y,x] = pic[y1,x1]
pic[y1,x1] = tmp
p0 = random.randint(100,104)
c0 = random.randint(200,204)
config = (p0,c0)
for x in range(w):
for y in range(h):
k = int(round(const*r3))%256
k = bin(k)[2:].ljust(8,'0')
k = int(k[p0%8:]+k[:p0%8],2)
r3 = f3(r3)
p0 = pic[y,x]
c0 = k^((k+p0)%256)^c0
pic[y,x] = c0
return pic,size,config
def outputImage(path,pic,size):
im = Image.new('P', size,'white')
pixels = im.load()
for i in range(im.size[0]):
for j in range(im.size[1]):
pixels[i,j] = (int(pic[j][i]))
im.save(path)
def decryptImage(pic,size,config):
.....
enc_img = 'flag.bmp'
out_im = 'flag_enc.bmp'
pic,size,_ = encryptImage(enc_img)
outputImage(out_im,pic,size)
I don't know why it didn't come out. I found the confusion function, and then encryption and decryption are very similar. Finally, I ran 6400 pictures and didn't solve it. Wait for WP; Scripts used
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from PIL import Image
from decimal import *
import numpy as np
getcontext().prec = 20
enc_img = 'flag.bmp'
out_im = 'flag_enc.bmp'
def f1(x):
# It is based on logistic map in chaotic systems
# The parameter r takes the largest legal value
x = 4 * x * (1-x)
assert(x >= 0)
assert(x <= 1)
return x
def outputImage(path, pic, size):
im = Image.new('P', size, 'white')
pixels = im.load()
for i in range(im.size[0]):
for j in range(im.size[1]):
pixels[i, j] = (int(pic[j][i]))
im.save(path)
def decryptImage(p1, config, p0x):
im = Image.open(out_im)
size = im.size
pic = np.array(im)
im.close()
r1 = Decimal('0.478706063089473894123')
r2 = Decimal('0.613494245341234672318')
r3 = Decimal('0.946365754637812381837')
w, h = size
rx1 = []
rx2 = []
rx3 = []
for i in range(200):
r1 = f1(r1)
r2 = f1(r2)
r3 = f1(r3)
rx1.append(r1)
rx2.append(r2)
rx3.append(r3)
for x in range(w-1, -1, -1):
for y in range(h-1, -1, -1):
r1 = f1(r1)
r2 = f1(r2)
r3 = f1(r3)
rx1.append(r1)
rx2.append(r2)
rx3.append(r3)
const = 10 ** 14
p0, c0 = config
for x in range(w-1, -1, -1):
for y in range(h-1, -1, -1):
k = int(round(const * r3)) % 256
k = bin(k)[2:].ljust(8, '0')
k = int(k[p0 % 8:] + k[:p0 % 8], 2)
rx3.pop()
r3 = rx3[-1]
p0 = p0x
c0 = k^((k+p0)%256)^c0
pic[y, x] = c0
for x in range(w-1, -1, -1):
for y in range(h-1, -1, -1):
x1 = int(round(const * r1)) % w
y1 = int(round(const * r2)) % h
rx1.pop()
rx2.pop()
r1 = rx1[-1]
r2 = rx2[-1]
tmp = pic[y, x]
pic[y, x] = pic[y1, x1]
pic[y1, x1] = tmp
outputImage(p1, pic, size)
i = 1
for p0 in range(100, 105):
for c0 in range(200, 205):
for p0xx in range(0, 256):
decryptImage(str(i)+'.bmp', (p0, c0), p0xx)
i += 1
After looking at the WP from the destiny team, it's still the problem of inverse algorithm. It's too simple to think that encryption is decryption. Just change it a little
Put forward the attitude of re, first cp write down the source code and write it down again
from PIL import Image
from decimal import *
import numpy as np
import random
getcontext().prec = 20
def f1(x):
assert (x >= 0)
assert (x <= 1)
return 4 * x * (1 - x)
def f2(x):
assert (x >= 0)
assert (x <= 1)
return 4 * x * (1 - x)
def f3(x):
assert (x >= 0)
assert (x <= 1)
return 4 * x * (1 - x)
im = Image.open('flag_enc.bmp')
size = im.size
pic = np.array(im)
im.close()
r1 = Decimal('0.478706063089473894123')
r2 = Decimal('0.613494245341234672318')
r3 = Decimal('0.946365754637812381837')
w, h = size
for i in range(200):
r1 = f1(r1)
r2 = f2(r2)
r3 = f3(r3)
const = 10 ** 14
p = [100, 101, 102, 103]
c = [200, 201, 202, 203]
R1, R2, R3 = r1, r2, r3
l1 = []
l2 = []
for i in range(w * h):
l1.append(r1)
l2.append(r2)
r1 = f1(r1)
r2 = f2(r2)
def decrypt(p0, c0, r1=R1, r2=R2, r3=R3):
for x in range(w):
for y in range(h):
k = int(round(const * r3)) % 256
k = bin(k)[2:].ljust(8, '0')
k = int(k[p0 % 8:] + k[:p0 % 8], 2)
r3 = f3(r3)
pic[y, x] = ((pic[y, x] ^ c0 ^ k) - k) % 256
p0 = pic[y, x]
c0 = k ^ ((k + p0) % 256) ^ c0
t = w * h - 1
for x in range(w - 1, -1, -1):
for y in range(h - 1, -1, -1):
x1 = int(round(const * l1[t])) % w
y1 = int(round(const * l2[t])) % h
tmp = pic[y, x]
pic[y, x] = pic[y1, x1]
pic[y1, x1] = tmp
t -= 1
return pic, size
enc_img = 'flag.bmp'
count = 0
for p0 in p:
for c0 in c:
pic, size = decrypt(p0, c0)
im = Image.new('P', size, 'white')
pixels = im.load()
for i in range(im.size[0]):
for j in range(im.size[1]):
pixels[i, j] = (int(pic[j][i]))
count += 1
im.save(str(count) + enc_img)
All right, I'm starting to reappear. It was really hasty in the game. Many points were not found
Well, I'm a waste. I feel like I'm finished, but I just can't get out; Just take a look at the master's, just one look. emmmmm, horizontal trough! I never thought I'd die here

Operation priority. XOR is not bracketed, which annoys you. It is recommended to copy the priority table a hundred times. The priority of bit operation is lower than addition and subtraction
Incidentally, I found that the master only exploded 16 cases
Then lie down to Wanquan kerosene Baode Baguio, because I came out with 25 flag s

#!/usr/bin/env python
# -*- coding: utf-8 -*-
from PIL import Image
from decimal import *
import numpy as np
getcontext().prec = 20
def f1(x):
# It is based on logistic map in chaotic systems
# The parameter r takes the largest legal value
assert (x >= 0)
assert (x <= 1)
x = 4 * x * (1 - x)
return x
def f2(x):
# same as f1
return f1(x)
def f3(x):
# same as f1
return f1(x)
def outputImage(path, pic, size):
im = Image.new('P', size,'white')
pixels = im.load()
for i in range(im.size[0]):
for j in range(im.size[1]):
pixels[i, j] = (int(pic[j][i]))
im.save(path)
def decryptImage(path, p0c0):
im = Image.open(in_img)
size = im.size
pic = np.array(im)
im.close()
r1 = Decimal('0.478706063089473894123')
r2 = Decimal('0.613494245341234672318')
r3 = Decimal('0.946365754637812381837')
w, h = size
const = 10 ** 14
for _ in range(200):
r1 = f1(r1)
r2 = f2(r2)
r3 = f3(r3)
r1_list, r2_list = [], []
for _ in range(w * h):
r1_list.append(r1)
r2_list.append(r2)
r1 = f1(r1)
r2 = f2(r2)
p0 = p0c0[0]
c0 = p0c0[1]
for x in range(w):
for y in range(h):
k = int(round(const * r3)) % 256
k = bin(k)[2:].ljust(8, '0')
k = int(k[p0 % 8:] + k[:p0 % 8], 2)
r3 = f3(r3)
pic[y, x] = ((pic[y, x] ^ c0 ^ k) - k) % 256
c0 = k ^ ((k + pic[y, x]) % 256) ^ c0
p0 = pic[y, x]
for x in range(w-1, -1, -1):
for y in range(h-1, -1, -1):
x1 = int(round(const*r1_list.pop())) % w
y1 = int(round(const*r2_list.pop())) % h
pic[y, x], pic[y1, x1] = pic[y1, x1], pic[y, x]
outputImage(path, pic, size)
in_img = 'flag_enc.bmp'
i = 1
for p in range(100, 105):
for c in range(200, 205):
decryptImage(str(i)+'.bmp', (p, c))
i += 1
UIUCTF 2021
Re-hvhpgs{synt}
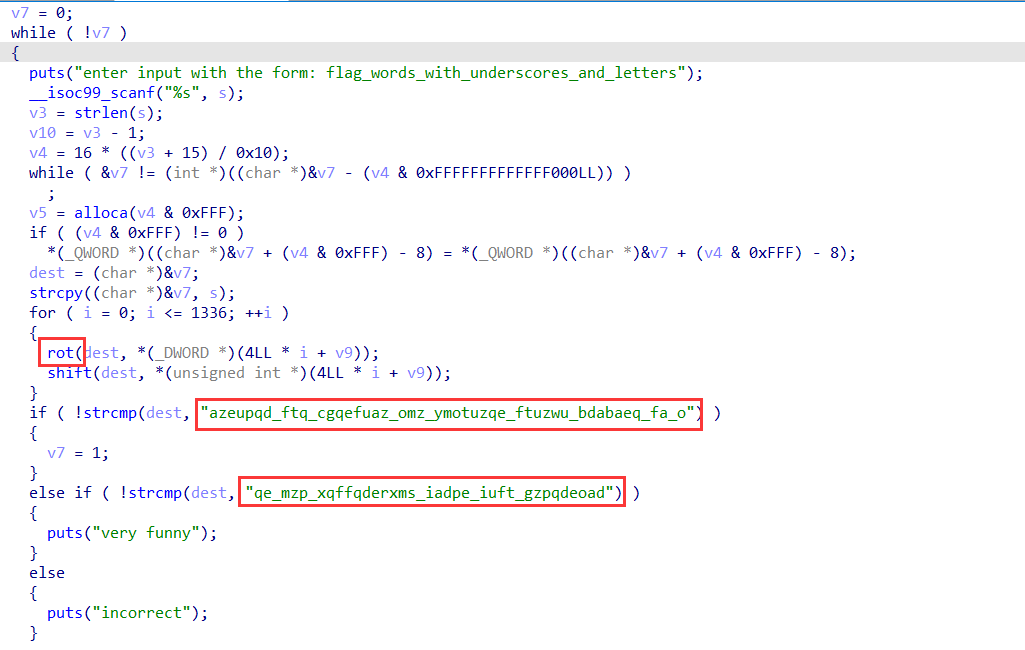
First, you can see the two most conspicuous strings of characters. After the word frequency, you can find meaningful characters. Then you can find that it is rot and displacement. Tear it directly by hand and enter i_propose_to_consider_the_question_can_machines_think to get the flag
Crypto-dhke_intro
Topic tips
Small numbers are bad in cryptography. This is why.
import random
from Crypto.Cipher import AES
# generate key
gpList = [ [13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29] ]
g, p = random.choice(gpList)
a = random.randint(1, p)
b = random.randint(1, p)
k = pow(g, a * b, p)
k = str(k)
# print("Diffie-Hellman key exchange outputs")
# print("Public key: ", g, p)
# print("Jotaro sends: ", aNum)
# print("Dio sends: ", bNum)
# print()
# pad key to 16 bytes (128bit)
key = ""
i = 0
padding = "uiuctf2021uiuctf2021"
while (16 - len(key) != len(k)):
key = key + padding[i]
i += 1
key = key + k
key = bytes(key, encoding='ascii')
with open('flag.txt', 'rb') as f:
flag = f.read()
iv = bytes("kono DIO daaaaaa", encoding = 'ascii')
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)
print(ciphertext.hex())
The hint is to exchange Diffie Hellman keys, but they can be exploded. Pay attention to the hex code. Catch a jo Chef
# !/usr/bin/env python
# -*- coding:utf-8 -*-
from Crypto.Cipher import AES
from binascii import unhexlify
ciphertext = 'b31699d587f7daf8f6b23b30cfee0edca5d6a3594cd53e1646b9e72de6fc44fe7ad40f0ea6'
gpList = [[13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29]]
iv = bytes("kono DIO daaaaaa", encoding='ascii')
for g, p in gpList:
for a in range(1, p+1):
for b in range(1, p+1):
k = str(pow(g, a * b, p))
key = ''
i = 0
padding = 'uiuctf2021uiuctf2021'
while 16 - len(key) != len(k):
key = key + padding[i]
i += 1
key = key + k
key = bytes(key, encoding='ascii')
cipher = AES.new(key, AES.MODE_CFB, iv)
flag = cipher.decrypt(unhexlify(ciphertext))
if flag.startswith(b'uiuctf'):
print(flag)
Crypto-back_to_basics
from Crypto.Util.number import long_to_bytes, bytes_to_long
from gmpy2 import mpz, to_binary
#from secret import flag, key
ALPHABET = bytearray(b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ#")
def base_n_encode(bytes_in, base):
return mpz(bytes_to_long(bytes_in)).digits(base).upper().encode()
def base_n_decode(bytes_in, base):
bytes_out = to_binary(mpz(bytes_in, base=base))[:1:-1]
return bytes_out
def encrypt(bytes_in, key):
out = bytes_in
for i in key:
print(i)
out = base_n_encode(out, ALPHABET.index(i))
return out
def decrypt(bytes_in, key):
out = bytes_in
for i in key:
out = base_n_decode(out, ALPHABET.index(i))
return out
"""
flag_enc = encrypt(flag, key)
f = open("flag_enc", "wb")
f.write(flag_enc)
f.close()
"""
Of course, there is a flag_ The ENC file and word are too big. You should bear it~
Very interesting topic. Master Shang woke me up, that is, the conversion of 2 ~ 36 base systems and the key functions
def base_n_decode(bytes_in, base): bytes_out = long_to_bytes(int(bytes_in, base=base)) return bytes_out
I have to say that python's int is quite perfect
Then I didn't write a one-time script and tore it by hand, because for example, the last digit of the key is W-ary, but U and V don't appear in the ciphertext. Isn't the script perfect
Crypto-dhke_adventure
It's also the problem of chef jo. It's obvious that the cipher problem of discrete logarithm system. Because hint has smoother, it can be thought of as the smooth number problem of dissociating discrete logarithm
from random import randint
from Crypto.Util.number import isPrime
from Crypto.Cipher import AES
from hashlib import sha256
print("I'm too lazy to find parameters for my DHKE, choose for me.")
print("Enter prime at least 1024 at most 2048 bits: ")
# get user's choice of p
p = input()
p = int(p)
# check prime valid
if p.bit_length() < 1024 or p.bit_length() > 2048 or not isPrime(p):
exit("Invalid input.")
# prepare for key exchange
g = 2
a = randint(2,p-1)
b = randint(2,p-1)
# generate key
dio = pow(g,a,p)
jotaro = pow(g,b,p)
key = pow(dio,b,p)
key = sha256(str(key).encode()).digest()
with open('flag.txt', 'rb') as f:
flag = f.read()
iv = b'uiuctf2021uiuctf'
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)
print("Dio sends: ", dio)
print("Jotaro sends: ", jotaro)
print("Ciphertext: ", ciphertext.hex())
Known
d i o = g a m o d p dio=g^a\ mod\ p dio=ga mod p
j o t a r o = g b m o d p jotaro=g^b\ mod\ p jotaro=gb mod p
k e y = d i o b m o d p key=dio^b\ mod\ p key=diob mod p
The key to solving the problem is that p can be provided by the attacker. It's good to directly provide a smooth number + 1. In this way, the problem of solving DLP discrete logarithm becomes computable. For specific derivation, refer to pohlig Hellman attack principle, which can be reproduced
Some small points are directly scripted here. First, a smooth number is generated
from Crypto.Util.number import *
from gmpy2 import *
item = 2
p = 1
while 1:
p *= item
item = next_prime(item)
if 1024 < p.bit_length() < 2048 and isPrime(p + 1):
print(p+1)
break
Lazy dog, directly receive manually, and then find a and b in sgae; you raise me up of WANGDING cup Qinglong group has been demonstrated before. The final script is as follows
#!/usr/bin/env python # -*- coding: utf-8 -*- from Crypto.Cipher import AES from binascii import unhexlify from hashlib import sha256 p = 20404068993016374194542464172774607695659797117423121913227131032339026169175929902244453757410468728842929862271605567818821685490676661985389839958622802465986881376139404138376153096103140834665563646740160279755212317501356863003638612390661668406235422311783742390510526587257026500302696834793248526734305801634165948702506367176701233298064616663553716975429048751575597150417381063934255689124486029492908966644747931 a = 1706514538409217609380184471483970486111601581179909732547081795755601848099714892783660477820125268651686071436129197042742970850298506167342840465201954449860957095450958345421698689291401652404764413822088773220645950460091121901749681603487210460064157239812734204314334694247020508700704643391774792654182943517813353983667531492481271292815208332729128642069655591289999915464139472699283049217926350224615448461688066 b = 14466632275269913037069509287532932279884213206515600538938395240468925268146374104530207395909468350257778074856758057525057561502009116834555962090895520108072724285442706303410135968614985268443945781896987070215220814783356743958044861941110284092061774699164461968593879814604175818707171934938878476262296832165434644133455246857171139473183371584687955863862012348287764247314297996868855594079156695942227229848338865 dio = 16167922424137241666246302388507094614219683075656937696624976269971219170930381539629329712953190516880647147637220034502113432117052541565403357952291692484827614380683288824529855182911429985823152492290185107775580207164746921109360997835543504066225649925051809637197356760554700827177215351020335554912004088973554778245562345835228507025035376705826984822212122075068467338353809039042992813485576139824709322511611135 assert dio == pow(g, a, p) assert jotaro == pow(g, b, p) key = pow(dio, b, p) key = sha256(str(key).encode()).digest() jo = 8478318935358501390014596426908185869306605857407596116840606911586830527583698320042764633027826654399751539088096707226001027141331485792640154020208368663060333097725346477808040686885134694513306486060638308544451042554707764114958622916238232491752753035945375341164707378481832386716731243612254449779955395389475168461403985894687650228947467124029857674022920610930987210652487673276585269753595356252512713370074208 ciphertext = 'f21c554f4e520e3122eb9708bd88de356b7d0d8d9728536b39d22b706afcdaecd7bed753666a763f8c0d' iv = b'uiuctf2021uiuctf' cipher = AES.new(key, AES.MODE_CFB, iv) flag = cipher.decrypt(unhexlify(ciphertext)) print(flag)
The newly configured windows terminal is really nice. It won't be disordered. Show it

Crypto CTF
At that time, it was over before I had time to fight, so I posted a flag on everything I made. Thank you. The organizers don't care
Sign in and don't say
Farm
#!/usr/bin/env sage
from sage.all import *
import string, base64, math
from flag import flag
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
def keygen(l):
key = [F[randint(1, 63)] for _ in range(l)]
key = math.prod(key) # Optimization the key length :D
return key
def maptofarm(c):
assert c in ALPHABET
return F[ALPHABET.index(c)]
def encrypt(msg, key):
m64 = base64.b64encode(msg)
enc, pkey = '', key**5 + key**3 + key**2 + 1
for m in m64:
enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
return enc
# KEEP IT SECRET
key = keygen(14) # I think 64**14 > 2**64 is not brute-forcible :P
enc = encrypt(flag, key)
print(f'enc = {enc}')
Originally, I saw that it was abandoned and set several layers. Isn't GF a finite field? How did it come out???
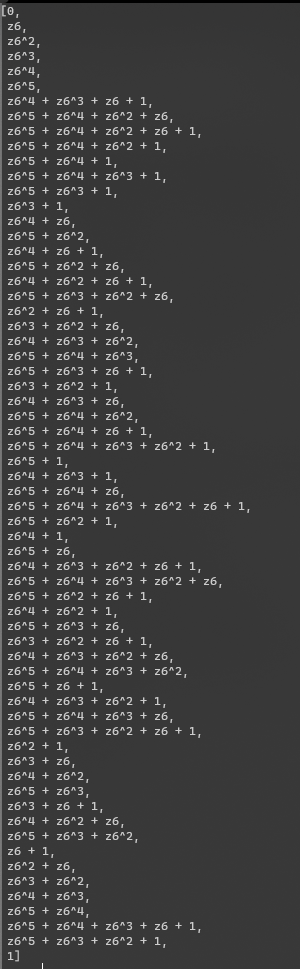
But now I want to reproduce it. I've hardened my head. I didn't expect to come out for the first time. It's similar to the relationship between dictionary key and value. Just blow up the key. Originally, I wanted to draw a flow chart, but that is, the replacement of some positions and values from the alphabet to f and F to the alphabet is not well reflected. Since it is a simple question, I won't draw it. Paste script
import string
import base64
enc = '805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj'
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
for pkey in F:
c = ''
for i in enc:
p1 = ALPHABET.index(i)
p2 = 0
if pkey!= 0:
p2 = F.index(F[p1] / pkey)
c += ALPHABET[p2]
try:
print(base64.b64decode(c))
except:
pass
Then find the flag in the 64 results
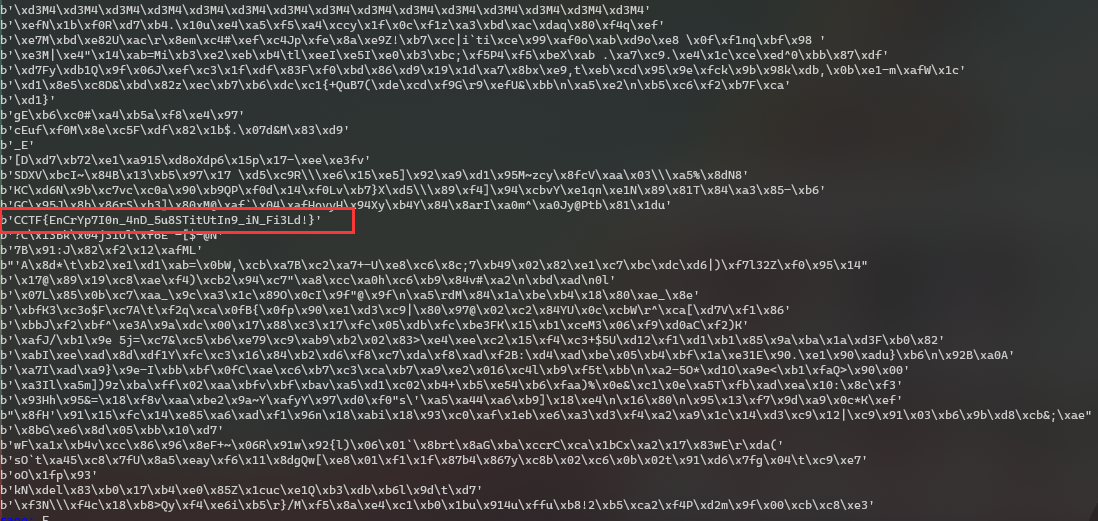
CCTF{EnCrYp7I0n_4nD_5u8STitUtIn9_iN_Fi3Ld!}