Master Shang is very handy with the problem of sophomore work abroad. He still needs to work hard

RARCTF

Note: the problem of not giving data is generally given an nc connection

Crypto-minigen

exec('def f(x):'+'yield((x:=-~x)*x+-~-x)%727;'*100)
g=f(id(f));print(*map(lambda c:ord(c)^next(g),list(open('f').read())))

281 547 54 380 392 98 158 440 724 218 406 672 193 457 694 208 455 745 196 450 724

Tips:

A stream cipher in only 122 bytes!
Note: This has been tested on python versions 3.8 and 3.9

The title is not long, but it is difficult to read such simplified python code. It is difficult to sign it under the guidance of master Shang

To know that exec, yield and id are mainly the three functions and the equivalent expression of taking the inverse sign ~ in python, baidu is recommended

After layers of analysis, finally extract such a stream cipher algorithm, of course, model 727

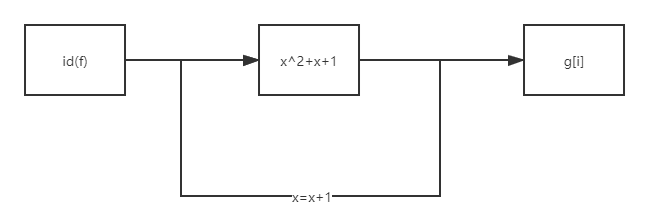
Then I wrote on the draft paper ( x + 1 ) 2 + ( x + 1 ) + 1 − x 2 − x − 1 = 2 x + 2 (x+1)^2+(x+1)+1-x^2-x-1=2x+2 (x+1)2+(x+1)+1 − x2 − x − 1=2x+2, and then I was really confused. I didn't expect it

Master Shang can see at a glance that if the initial state of an id(f), or stream cipher, is fixed in different IDS (f), the difference between the two iterators g is fixed

For example, take a chestnut, for example, id(f)=1, then the difference between each g is 4 6 8 10 12... In turn, and the whole space is under module 727, so the blasting is also within the scope of blasting

However, there is no need to explode. Suppose that the beginning of the flag is' rarctf ', then let's XOR back. The first six values of G are 363 578 68 287 508 respectively. We can see that the difference between them is 215 217 219 221 223 in turn, and then go back. It's not easy to get g, XOR back

#!/usr/bin/env python
# -*- coding: utf-8 -*-
exec('def f(x):'+'yield((x:=-~x)*x+-~-x)%727;'*100)
# print(*map(lambda c:ord(c)^next(g),list(open('f').read())))
# ((x:=-~x)*x+-~-x)%727
c = '281 547 54 380 392 98 158 440 724 218 406 672 193 457 694 208 455 745 196 450 724'
flag = ''
fi = []
for i in c.split(' '):
    fi.append(int(i))
flag = 'r'
s = 363
x = 0
for i in fi[1:]:
    flag += chr((s + 215 + 2 * x) % 727 ^ i)
    s = (s+215+2*x) % 727
    x += 1
print(flag)

Thank Master Shang again for taking me to CTF

Crypto-sRSA

from Crypto.Util.number import *

p = getPrime(256)
q = getPrime(256)
n = p * q
e = 0x69420

flag = bytes_to_long(open("flag.txt", "rb").read())
print("n =",n)
print("e =", e)
print("ct =",(flag * e) % n)

n = 5496273377454199065242669248583423666922734652724977923256519661692097814683426757178129328854814879115976202924927868808744465886633837487140240744798219
e = 431136
ct = 3258949841055516264978851602001574678758659990591377418619956168981354029697501692633419406607677808798749678532871833190946495336912907920485168329153735

Using the similar idea of ElGamal, directly find the inverse element

from flag import flag

print(flag)

Just have a hand

Crypto-unrandompad

from random import getrandbits
from Crypto.Util.number import getPrime, long_to_bytes, bytes_to_long

def keygen(): # normal rsa key generation
  primes = []
  e = 3
  for _ in range(2):
    while True:
      p = getPrime(1024)
      if (p - 1) % 3:
        break
    primes.append(p)
  return e, primes[0] * primes[1]

def pad(m, n): # pkcs#1 v1.5
  ms = long_to_bytes(m)
  ns = long_to_bytes(n)
  if len(ms) >= len(ns) - 11:
    return -1
  padlength = len(ns) - len(ms) - 3
  ps = long_to_bytes(getrandbits(padlength * 8)).rjust(padlength, b"\x00")
  return int.from_bytes(b"\x00\x02" + ps + b"\x00" + ms, "big")

def encrypt(m, e, n): # standard rsa
  res = pad(m, n)
  if res != -1:
    print(f"c: {pow(m, e, n)}")
  else:
    print("error :(", "message too long")

menu = """
[1] enc()
[2] enc(flag)
[3] quit
"""[1:]

e, n = keygen()
print(f"e: {e}")
print(f"n: {n}")
while True:
  try:
    print(menu)
    opt = input("opt: ")
    if opt == "1":
      encrypt(int(input("msg: ")), e, n)
    elif opt == "2":
      encrypt(bytes_to_long(open("/challenge/flag.txt", "rb").read()), e, n)
    elif opt == "3":
      print("bye")
      exit(0)
    else:
      print("idk")
  except Exception as e:
    print("error :(", e)

Yeah I use randomized padding, it increases security!

Note: This is a part 1 challenge of randompad. Take a look at the source for that one and compare the two for a hint on how to solve.

Prompt to audit the code of another topic. If you find something very interesting, you should look carefully

Although this problem has a pad function, it does not work on M and directly encrypts m, so the attack point of the problem can only be on e=3 (because I p − 1 = 3 k + 1 p-1=3k+1 p − 1=3k+1 (no clue obtained)

Then I was also very XOR. I watched a radio attack for a long time. I was really distracted and thought too complicated; There's nothing to say after knowing it's a broadcast

In addition, this type of topic is really better than giving three groups directly ( c i ,   n i ) (c_i,\ n_i) (ci, ni) it's good to be a lot more obscure

from flag import flag

print(flag)

Crypto-babycrypt

from Crypto.Util.number import getPrime, bytes_to_long

flag = bytes_to_long(open("/challenge/flag.txt", "rb").read())

def genkey():
    e = 0x10001
    p, q = getPrime(256), getPrime(256)
    if p <= q:
      p, q = q, p
    n = p * q
    pubkey = (e, n)
    privkey = (p, q)
    return pubkey, privkey

def encrypt(m, pubkey):
    e, n = pubkey
    c = pow(m, e, n)
    return c

pubkey, privkey = genkey()
c = encrypt(flag, pubkey)

hint = pubkey[1] % (privkey[1] - 1)
print('pubkey:', pubkey)
print('hint:', hint)
print('c:', c)

Master wuwushang's belt

The meaning of the topic is very clear. There is only one attack point
h i n t = n % ( q − 1 )   And   p > = q hint=n\%(q-1) \ and \ P > = q hint=n%(q − 1) and P > = q
I don't have any ideas and always want to rely on dp leakage; But this question looks familiar. I remember master Shang said something similar, using congruence and the nature of division

Let's start reproducing

Replace n with another expression, according to the nature of congruence a ≡ b   ( m o d   n ) And c ≡ d   ( m o d   n ) ,   be a + b ≡ c + d   ( m o d   n ) a\equiv b\ (mod\ n) and c\equiv d\ (mod\ n), \ then a+b\equiv c+d\ (mod\ n) A ≡ b (mod n) and c ≡ d (mod n), then a+b ≡ c+d (mod n), which is equivalent to the reverse
n % ( q − 1 ) = ( ( p − 1 ) ( q − 1 ) + ( p + q − 1 ) ) % ( q − 1 ) = ( p + q − 1 ) % ( q − 1 ) = p % ( q − 1 ) n\%(q-1)=((p-1)(q-1)+(p+q-1))\%(q-1)=(p+q-1)\%(q-1)=p\%(q-1) n%(q−1)=((p−1)(q−1)+(p+q−1))%(q−1)=(p+q−1)%(q−1)=p%(q−1)
Then bring in hint
h i n t = p % ( q − 1 ) hint=p\%(q-1) hint=p%(q−1)
Namely
p = k ( q − 1 ) + h i n t p=k(q-1)+hint p=k(q−1)+hint
It is known from the condition that p is larger than q, so let's assume that k is positive and the same number of bits, k will not be large and can explode

Given n, replace p
n / q = k ( q − 1 ) + h i n t n = k ( q 2 − q ) + h i n t × q n/q=k(q-1)+hint\\ n=k(q^2-q)+hint\times q n/q=k(q−1)+hintn=k(q2−q)+hint×q
Obviously, you can solve a quadratic equation of one variable
k q 2 + ( h i n t − k ) q − n = 0 kq^2+(hint-k)q-n=0 kq2+(hint−k)q−n=0
judge Δ = ( h i n t − k ) 2 + 4 k n \Delta =(hint-k)^2+4kn Δ= (hint − k)2+4kn, or directly use sage or python library to solve the equation. It is poorly written during the game, but it seems that k=1 can be solved

Master Shang yyds

In other words, I think nq leakage should also be regarded as a classic rsa attack, but it is rarely seen on the Internet

Crypto-Shamir's Stingy Sharing

import random, sys
from Crypto.Util.number import long_to_bytes

def bxor(ba1,ba2):
	return bytes([_a ^ _b for _a, _b in zip(ba1, ba2)])

BITS = 128
SHARES = 30

poly = [random.getrandbits(BITS) for _ in range(SHARES)]
flag = open("/challenge/flag.txt","rb").read()

random.seed(poly[0])
print(bxor(flag, long_to_bytes(random.getrandbits(len(flag)*8))).hex())

try:
	x = int(input('Take a share... BUT ONLY ONE. '))
except:
	print('Do you know what an integer is?')
	sys.exit(1)
if abs(x) < 1:
	print('No.')
else:
	print(sum(map(lambda i: poly[i] * pow(x, i), range(len(poly)))))

XOR, the encryption function is the decryption function; Need to know random Getrandbits (len (flag) * 8), that is, you need to know the random seed poly[0]

The SHARES given is relatively small, so it should not be the restoration of Mason's rotating random number; Known

sum(map(lambda i: poly[i] * pow(x, i), range(len(poly))))

Namely
∑ i = 0 29 p o l y [ i ] × x i \sum_{i=0}^{29}poly{[i]}\times x^i i=0∑29​poly[i]×xi
X is our input. Obviously, when x=1, the output is the sum of poly
p o l y [ 0 ] + p o l y [ 1 ] + p o l y [ 2 ] + p o l y [ 3 ] + ... + p o l y [ 29 ] poly[0]+poly[1]+poly[2]+poly[3]+...+poly[29] poly[0]+poly[1]+poly[2]+poly[3]+...+poly[29]
If we know
p o l y [ 0 ] + p o l y [ 1 ] × 2 + p o l y [ 2 ] × 2 2 + p o l y [ 3 ] × 2 3 + ... + p o l y [ 29 ] × 2 29 poly[0]+poly[1]\times 2+poly[2]\times 2^2+poly[3]\times 2^3+...+poly[29]\times 2^{29} poly[0]+poly[1]×2+poly[2]×22+poly[3]×23+...+poly[29]×229
Wait for a series of, it is estimated that we can do something; Unfortunately, the same set of poly can only find polynomials about an x

It took a long time to find the attack on Shamir in la Lao's blog. Other attacks are basically some implementation processes

Set poly[0] to s 1 s_1 s1, poly[0]+2 is s 2 s_2 s2​， p o l y [ 1 ] + p o l y [ 2 ] + p o l y [ 3 ] + ... + p o l y [ 29 ] poly[1]+poly[2]+poly[3]+...+poly[29] poly[1]+poly[2]+poly[3] +... + poly[29] is A, p, and we have A 256 bit prime number
s 1 + A − f ( x ) 1 ≡ 0   ( m o d   p ) s 2 + A − f ( x ) 2 ≡ 0   ( m o d   p ) s 1 + 2 − s 2 ≡ 0   ( m o d   p ) s_1+A-f(x)_1\equiv 0\ (mod\ p)\\ s_2+A-f(x)_2\equiv 0\ (mod\ p)\\ s_1+2-s_2\equiv 0\ (mod\ p) s1​+A−f(x)1​≡0 (mod p)s2​+A−f(x)2​≡0 (mod p)s1​+2−s2​≡0 (mod p)

#Sage
a = 1
b = 2


y1 = 4597744014826739716773723494617979066503
y2 = y1 + 2
PR.<s1,s2,A> = PolynomialRing(Zmod(p))
f1 = s1 + A - y1
f2 = s2 + A - y2
f3 = a * s1 + b - s2
Fs = [f1, f2, f3]
I = Ideal(Fs)
B = I.groebner_basis()
print('s1 =', ZZ(-B[0](0, 0, 0)))
print('s2 =', ZZ(-B[1](0, 0, 0)))

emmmmm sure enough, cheating is not the right way. There is only one equation. No matter how it changes, it can not become a system of equations

Finally, master Shang reminded me that master Shang is supernatural

Don't you want to know the first place? We might as well give x 1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Yes, every value of poly is exposed

The title here won't be Shamir's 0day, kidding XD

Write a small script for the rest and set the random number

import random
from Crypto.Util.number import *


def bxor(ba1, ba2):
    return bytes([_a ^ _b for _a, _b in zip(ba1, ba2)])


cipher = '6068879a5da40b08757b59a3924302244a52c2162505e531ccd061739e03d2'

ploy0 =  324624027062034109200467879481074306259
for k in range(10, 1000):
    random.seed(ploy0)
    print(bxor(long_to_bytes(int(cipher, 16)), long_to_bytes(random.getrandbits(k * 8))))

Crypto-rotoRSA(unsolved)

from sympy import poly, symbols
from collections import deque
import Crypto.Random.random as random
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes

def build_poly(coeffs):
    x = symbols('x')
    return poly(sum(coeff * x ** i for i, coeff in enumerate(coeffs)))

def encrypt_msg(msg, poly, e, N):
    return long_to_bytes(pow(poly(msg), e, N)).hex()

p = getPrime(256)
q = getPrime(256)
N = p * q
e = 11

flag = bytes_to_long(open("/challenge/flag.txt", "rb").read())

coeffs = deque([random.randint(0, 128) for _ in range(16)])


welcome_message = f"""
Welcome to RotorSA!
With our state of the art encryption system, you have two options:
1. Encrypt a message
2. Get the encrypted flag
The current public key is
n = {N}
e = {e}
"""

print(welcome_message)

while True:
    padding = build_poly(coeffs)
    choice = int(input('What is your choice? '))
    if choice == 1:
        message = int(input('What is your message? '), 16)
        encrypted = encrypt_msg(message, padding, e, N)
        print(f'The encrypted message is {encrypted}')
    elif choice == 2:
        encrypted_flag = encrypt_msg(flag, padding, e, N)
        print(f'The encrypted flag is {encrypted_flag}')
    coeffs.rotate(1)

ECC was a little hard and didn't go on

Re-verybabyrev

Check the SEC and find that it is a small end sequence, which is very important. Later, I reverse the sequence everywhere in s1

int __cdecl __noreturn main(int argc, const char **argv, const char **envp)
{
  __int64 s1[12]; // [rsp+0h] [rbp-100h] BYREF
  char v4; // [rsp+60h] [rbp-A0h]
  char s[140]; // [rsp+70h] [rbp-90h] BYREF
  int i; // [rsp+FCh] [rbp-4h]

  setvbuf(stdout, 0LL, 2, 0LL);
  memset(s, 0, 0x80uLL);
  s1[0] = 'EH\x1D\x12\x17\x11\x13\x13';
  s1[1] = '\t_B,&\vAE';
  s1[2] = 'T\x1BVV=l_\v';
  s1[3] = 'X\\\v<)EA_';
  s1[4] = '@*lT\t]_\0';
  s1[5] = 'K_BH\'j\x06\x06';
  s1[6] = 'l^]C,-BV';
  s1[7] = 'k1^CG\aA-';
  s1[8] = '^TI\x1Cn;\nZ';
  s1[9] = '((G^\x054+\x1A';
  s1[10] = '\x06\x04P\a;&\x11\x1F';
  s1[11] = '\nwH\x03\x05\v\r\x04';
  v4 = 0;
  printf("Enter your flag: ");
  fgets(s, 128, stdin);
  i = 0;
  if ( s[0] != 114 )
  {
    puts("Nope!");
    exit(0);
  }
  while ( i <= 126 )
  {
    s[i] ^= s[i + 1];
    ++i;
  }
  if ( !memcmp(s1, s, 97uLL) )
  {
    puts("Correct!");
    exit(1);
  }
  puts("Nope!");
  exit(0);
}

Then it's also like a stream password with an initial state. Just XOR back in turn

kw, scr1pt Master said that my code was ugly. I was so angry that I robbed his flag

#!/usr/bin/env python
# -*- coding: utf-8 -*-
s1 = b''
s1 += b'EH\x1D\x12\x17\x11\x13\x13'[::-1]
s1 += b'\t_B,&\vAE'[::-1]
s1 += b'T\x1BVV=l_\v'[::-1]
s1 += b'X\\\v<)EA_'[::-1]
s1 += b'@*lT\t]_\0'[::-1]
s1 += b'K_BH\'j\x06\x06'[::-1]
s1 += b'l^]C,-BV'[::-1]
s1 += b'k1^CG\aA-'[::-1]
s1 += b'^TI\x1Cn;\nZ'[::-1]
s1 += b'((G^\x054+\x1A'[::-1]
s1 += b'\x06\x04P\a;&\x11\x1F'[::-1]
s1 += b'\nwH\x03\x05\v\r\x04'[::-1]
s1 = s1.decode()
flag = 'r'
t = chr(ord(s1[0]) ^ ord('r'))
for i in s1[1:]:
    flag += t
    t = chr(ord(i) ^ ord(t))
print(flag)

But then again, although re is an inverse algorithm, there are still some operations such as shelling, which can't be started soon. After reading the second question, I gave up

Bsides Noida CTF

Crypto-Xoro(unsolved)

#!/usr/bin/env python3
import os

FLAG = open('flag.txt','rb').read()

def xor(a, b):
    return bytes([i^j for i,j in zip(a,b)])

def pad(text, size):
    return text*(size//len(text)) + text[:size%len(text)]

def encrypt(data, key):
    keystream = pad(key, len(data))
    encrypted = xor(keystream, data)
    return encrypted.hex()


if __name__ == "__main__":
    print("\n===== WELCOME TO OUR ENCRYPTION SERVICE =====\n")
    try:
        key = os.urandom(32)
        pt = input('[plaintext (hex)]>  ').strip()
        ct = encrypt(bytes.fromhex(pt) + FLAG, key)
        print("[ciphertext (hex)]>", ct)
        print("See ya ;)")
    except Exception as e:
        print(":( Oops!", e)
        print("Terminating Session!")

No, I got a pad. I read the WP on CTFTIME. It's still too easy to read the code by myself

pad doesn't go deep, but fills the key to the same length as pt+flag, so it's very simple

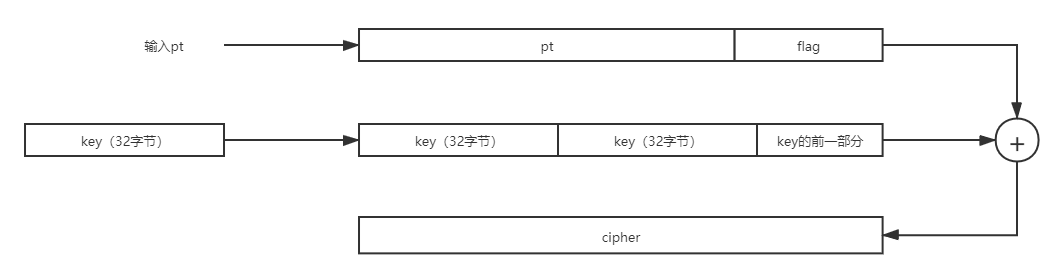
According to cipher and our own pt, we can get the key

Just know that a byte is equivalent to two characters, so know that the length of key and pt is at least 64 characters long

#!/usr/bin/env python
# -*- coding: utf-8 -*-
def xor(a, b):
    return bytes([i ^ j for i, j in zip(a, b)])


def pad(text, size):
    return text*(size//len(text)) + text[:size % len(text)]


def encrypt(data, key):
    keystream = pad(key, len(data))
    encrypted = xor(keystream, data)
    return encrypted

pt = '4'*64
cipher = 'b4547524f42baec143f1d9cb57e3d35eff4b7f3e13f551a2cb0eb73600d6ac1bb2437f0fd90b8bfe6fdaead070c6f945c2604e2535c37087e415a73a01cdb010a24f0e418f4e97'
key = xor(bytes.fromhex(pt), bytes.fromhex(cipher)[:32])
print(encrypt(bytes.fromhex(cipher), key))

Even stuck on the pad, there are still too few topics in cryptography

Crypto-MACAW

#!/usr/bin/env python3
from topsecrets import iv, key, secret_msg, secret_tag, FLAG
from Crypto.Cipher import AES

iv = bytes.fromhex(iv)

menu = """
/===== MENU =====\\
|                |
|  [M] MAC Gen   |
|  [A] AUTH      |
|                |
\================/
"""

def MAC(data):    
    assert len(data) % 16 == 0, "Invalid Input"
    assert data != secret_msg, "Not Allowed!!!"

    cipher = AES.new(key, AES.MODE_CBC, iv)
    tag = cipher.encrypt(data)[-16:]
    return tag.hex()

def AUTH(tag):
    if tag == secret_tag:
        print("[-] Successfully Verified!\n[-] Details:", FLAG)
    else:
        print("[-] Verification Flaied !!!")

if __name__ == "__main__":
    print(secret_msg)
    try:
        for _ in range(3):
            print(menu)
            ch = input("[?] Choice: ").strip().upper()
            if ch == 'M':
                data = input("[+] Enter plaintext(hex): ").strip()
                tag = MAC(bytes.fromhex(data))
                print("[-] Generated tag:", tag)
                print("[-] iv:", iv.hex())
            elif ch == 'A':
                tag = input("[+] Enter your tag to verify: ").strip()
                AUTH(tag)
            else:
                print("[!] Invalid Choice")
                exit()
    except Exception as e:
        print(":( Oops!", e)
        print("Terminating Session!")

Why are MACAWS becoming Another Endangered Species?

AES，CBC； Take out the DAS check-in diagram

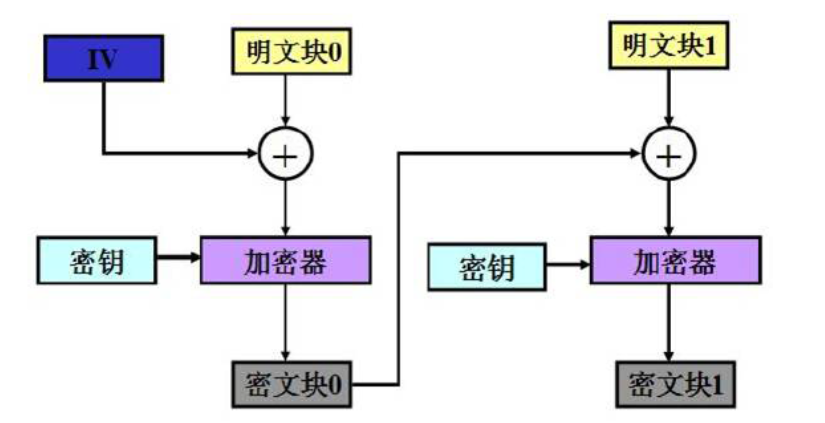
Huh? This topic, 50Solves?

As long as data = = secret_ Just MSG

assert data != secret_msg, "Not Allowed!!!"

So obviously, look at the first paragraph of the main function, secret_msg is Welcome to BSidesNoida!! Follow us on Twitter...， Then turn the hexadecimal code; I don't quite understand the logic of the code, but send the tag to get the flag BSNoida{M4c4w5_4r3_4d0r4b13}

a few moments later

I take back what I said just now. The above analysis is wrong, not just data == secret_msg is good, but data= secret_msg, but the real secret_msg also has a / N, and if you add \ n, the first condition is not satisfied

So to sum up, I don't know whether the person who created the title did it intentionally or inadvertently, and it was blindly jb made by me. It can also be called a check-in title (in order to prove that I made an exception, I gave flag;))

Crypto-Macaw_Revenge

Well, it was to pave the way for this problem

#!/usr/bin/env python3
from Crypto.Cipher import AES
import os

with open('flag.txt') as f:
    FLAG = f.read()


menu = """
/===== MENU =====\\
|                |
|  [M] MAC Gen   |
|  [A] AUTH      |
|                |
\================/
"""

def MAC(data, check=False):    
    assert len(data) % 16 == 0, "Invalid Input"

    if check:
        assert data != secret_msg, "Not Allowed!!!"

    cipher = AES.new(key, AES.MODE_CBC, iv)
    tag = cipher.encrypt(data)[-16:]
    return tag.hex()

def AUTH(tag):
    if tag == secret_tag:
        print("[-] Successfully Verified!\n[-] Details:", FLAG)
    else:
        print("[-] Verification Flaied !!!")

if __name__ == "__main__":
    iv = os.urandom(16)
    key = os.urandom(16)
    secret_msg = os.urandom(48)
    secret_tag = MAC(secret_msg)

    print(f"[+] Forbidden msg: {secret_msg.hex()}")
    try:
        for _ in range(3):
            print(menu)
            ch = input("[?] Choice: ").strip().upper()
            if ch == 'M':
                data = input("[+] Enter plaintext(hex): ").strip()
                tag = MAC(bytes.fromhex(data), check=True)
                print("[-] Generated tag:", tag)
                print("[-] iv:", iv.hex())
            elif ch == 'A':
                tag = input("[+] Enter your tag to verify: ").strip()
                AUTH(tag)
            else:
                print("[!] Invalid Choice")
                exit()
    except Exception as e:
        print(":( Oops!", e)
        print("Terminating Session!")

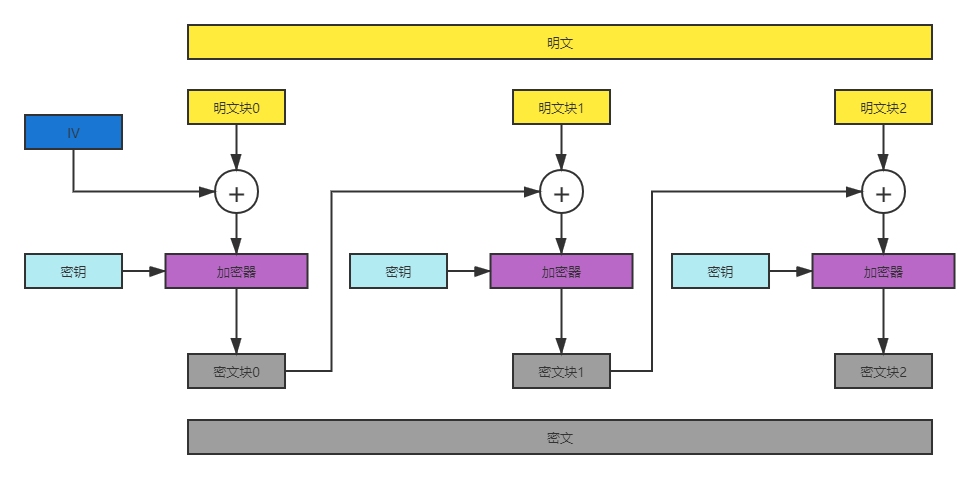
The above picture is not taken in vain. The test site CBC has no attack techniques. It is completely a transformation of the flow chart

There are two methods. It's still a headache to interact with pwntools. When you do it, you tear it directly with your hand

This is the first secret_tag = MAC(secret_msg) process

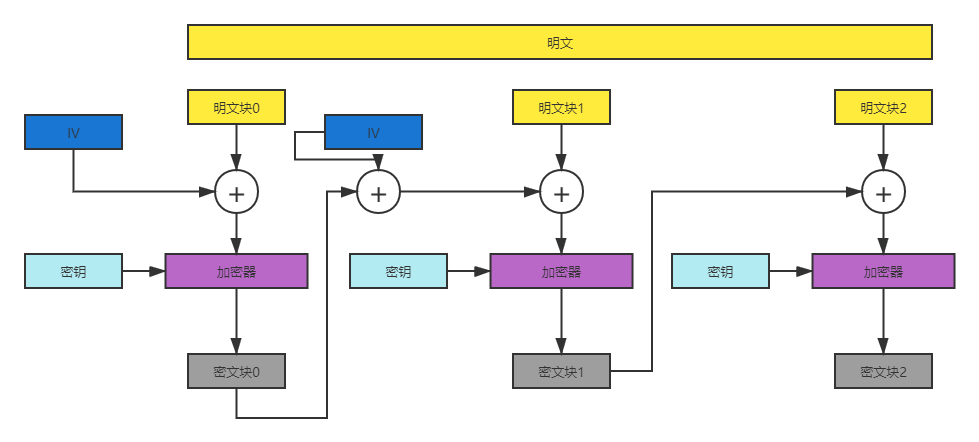
If plaintext is known, ciphertext block 2 is required; If we can get the third encryption offset IV ', we can get ciphertext block 2 by putting it into AES encryption

The first approach

Send plaintext block 0 to XOR for the first time, XOR the obtained ciphertext block 0 with known IV and plaintext block 1, then splice the obtained results to plaintext block 2 and send it to AES for encryption. Ciphertext block 2 will be input at the third verify to obtain flag

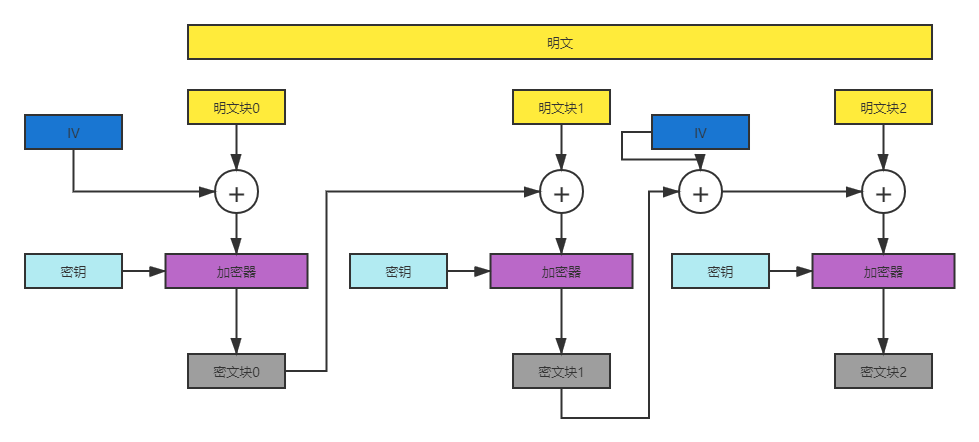
Another approach is similar. The plaintext blocks 0 and 1 are combined for the first encryption

The script is too ugly to show

The block password is still very interesting. Don't be rejected because you don't understand the encryption process of DES and AES

Crypto-baby_crypto

from functools import reduce
from operator import mul
from secrets import token_bytes
from sys import exit

from Crypto.Util.number import bytes_to_long, getPrime, long_to_bytes


def main():
	a = getPrime(512)
	b = reduce(mul, [getPrime(64) for _ in range(12)])
	flag = open("flag.txt", 'rb').read()
	flag_int = bytes_to_long(flag + token_bytes(20))
	if flag_int > b:
		print("this was not supposed to happen")
		exit()
	print("Try decrypting this =>", pow(flag_int, a, b))
	print("Hint =>", a)
	print("Thanks for helping me test this out,")
	print("Now try to break it")
	for _ in range(2):
		inp = int(input(">>> "))
		if inp % b in [0, 1, b - 1]:
			print("No cheating >:(")
			exit()
		res = pow(flag_int, inp * a, b)
		print(res)
		if res == 1:
			print(flag)


if __name__ == "__main__":
	try:
		main()
	except Exception:
		print("oopsie")

Like RSA's n unknown, I searched it casually and found it on the wiki RSA select plaintext attack , it's easy to understand

Now there are two ways in front of us. Because we can only cycle twice, after using the selective plaintext attack, we can't continue to change res into 1 according to the idea of the topic

I prefer to play directly

As long as b can be decomposed, we can definitely get a good decomposition. Although factordb is not decomposed this time (I didn't expect to decompose the smooth number), yafu and elliptic curve are decomposed

#!/usr/bin/env python
# -*- coding: utf-8 -*-
from functools import reduce
from operator import mul
from Crypto.Util.number import long_to_bytes
from gmpy2 import *


c = 20203085489987560014293976792631284029865794716340199579184268249383267835221417646400206440280554986191046482410144704655493648278552773961629440429092902828200586765600142014056717474264892592819336816357109261631354026033919601
a = 9199145544343906785257237030819067819650706729960940719583789075672838085664891493875966859020683165873915514690329495098632224089726035146839813982911647
res1 = 11556035784052138857307507506198973288367411883788209466242603646975181772393709048116382813114147667439254757077994923530326940311774811806341624846606432421390147764067475588289999480688178793625567838893122456687987320482961046
res2 = 31851104354654545190670904771335276903093012765843101980283420984000643289499190154554669289569530261009163188908584430876887966331849339667406478926717953660650120468017201255286785290943940825754781159249398489654218469154878634
# b = gcd(c**2-res1, c**3-res2)
b = 35928904747031491940426212169291743107379982701504027058404714745969854722708017688279836779414010447803620033738718602141821905862755021890356381265244649437631255336699627199559173294827426763360743177116198238833752565119866603
p1 = 9663156357322877677
p2 = 17687198236208397641
p3 = 13483379498110779557
p4 = 9827362203600815249
p5 = 16048195073366111129
p6 = 9608504155966563959
p7 = 17592003464121633761
p8 = 16940133308409174757
p9 = 10013743477508178887
p10 = 18085688756284030699
p11 = 15237723747921143731
p12 = 12510206954070273583
p = []
for i in range(1, 13):
    p.append(eval('p'+str(i)))
assert b == reduce(mul, [_ for _ in p])
phi = reduce(mul, [_-1 for _ in p])
d = invert(a, phi)
flag_int = long_to_bytes(pow(c, d, b))
print(flag_int)

I didn't try anything else

Ask yourself, is this problem only 22 solved? It seems that there are not many contestants

summary

These questions are done quickly. Although they are not long, the test site is very flexible, but it is still necessary to reproduce them even after the game. Take advantage of the target machine; However, there is a pitiful lack of cryptography in China. If you want to make a living, you still have to learn pwn

In addition, I learned a conversion between byte and hexadecimal coding that waiguoren likes very much, and xor operation of bytes with xor in pwntools

from pwn import xor

xor(bytes.fromhex(STRING1), bytes.fromhex(STRING2)).hex()