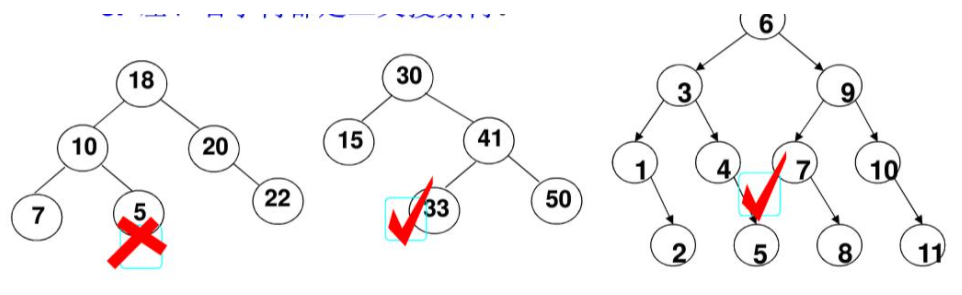
1. Binary search tree
- definition
Binary search tree (BST) is also called binary sort tree or binary lookup tree
Binary search tree: a binary tree, which can be empty;
If it is not empty, the following properties are met:
- All key values of non empty left subtree are less than those of its root node
- All key values of non empty right subtree are greater than those of its root node
- Both the left and right subtrees are binary search trees
2. Abstract data
2.1 special functions
#include<iostream>
#include<malloc.h>
using namespace std;
typedef int ElementType;
typedef struct TreeNode *BinTree;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree Find(ElementType X,BinTree BST): From binary search tree BST Find elements in X,Returns the address of the node where it is located
BinTree FindMin(BinTree BST): From binary search tree BST Find and return the address of the node where the smallest element is located
BinTree FindMax(BinTree BST): From binary search tree BST Finds and returns the address of the node where the largest element is located
BinTree Insert(ElementType X,BinTree BST): Insert an element BST
BinTree Delete(ElementType X,BinTree BST): from BST Delete an element from
2.2 search
- The search starts from the root node. If the tree is empty, NULL is returned
- If the search tree is not empty, the key value of the root node is compared with X and processed differently:
*If X is less than the key value of the root node, continue to search in the left subtree
*If X is greater than the key value of the root node, continue to search in the right subtree
*If X is equal to the key value of the root node, the search ends and a pointer to this node is returned - Find maximum and minimum elements
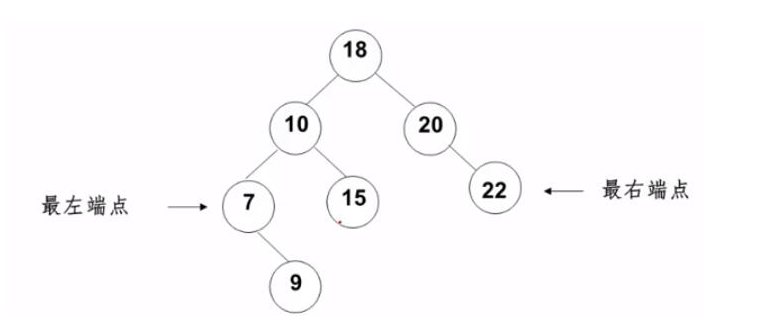
*The largest element must be on the end node of the rightmost branch of the tree
*The smallest element must be on the end node of the leftmost branch of the tree
2.2.1 search recursive implementation

// Find recursive implementation
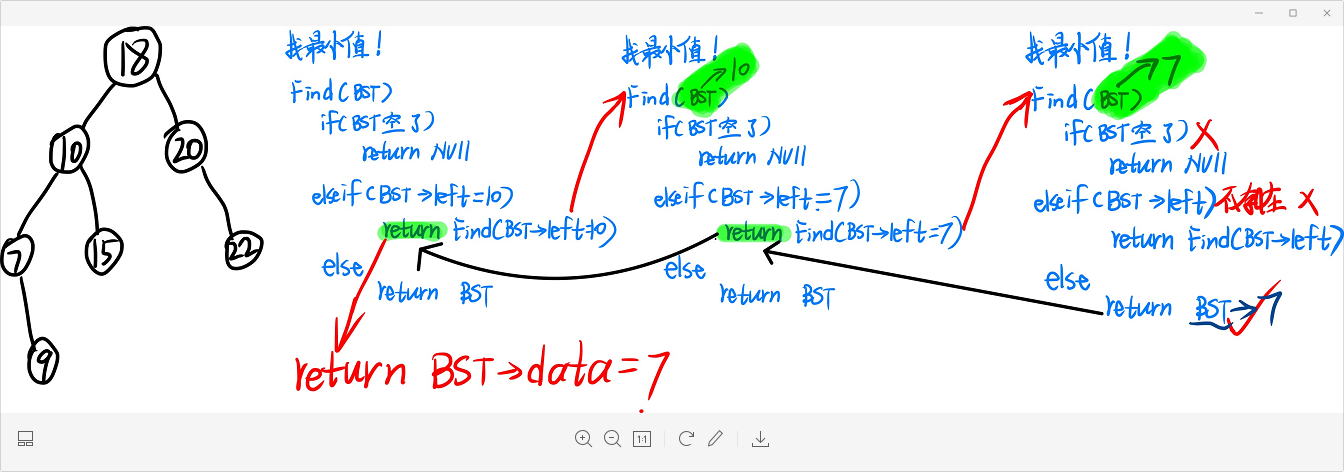
BinTree Find(ElementType X,BinTree BST){
if(!BST) // If the root node is empty, NULL is returned
return NULL;
if(X < BST->Data) // Smaller than the root node, go to the left subtree to find
return Find(X,BST->Left);
else if(BST->Data < X) // Larger than the root node, go to the right subtree to find
return Find(X,BST->Right);
else if(BST->Data == X) // eureka
return BST;
}
- Recursive implementation of finding minimum value
// Recursive implementation of finding minimum value
BinTree FindMin(BinTree BST){
if(!BST) // If it is empty, NULL is returned
return NULL;
else if(BST->Left) // There is also a left subtree. Continue to find along the left branch
return FindMin(BST->Left);
else // eureka
return BST;
}
2.2.2 find non recursive implementation
// Find non recursive implementation
BinTree IterFind(ElementType X,BinTree BST){
while(BST){
if(X < BST->Data)
BST = BST->Left;
else if(BST->Data < X) // Larger than the root node, go to the right subtree to find
BST = BST->Right;
else if(BST->Data == X) // eureka
return BST;
}
return NULL;
}
- Non recursive implementation of finding maximum
// Non recursive implementation of finding maximum
BinTree FindMax(BinTree BST){
if(BST) // If not empty
while(BST->Right) // As long as the right subtree still exists
BST = BST->Right;
return BST;
}
2.3 deletion
- Three cases of deletion:
1. The leaf node to be deleted: delete it directly and set its parent node pointer to NULL
2. The node to be deleted has only one child node: point the pointer of its parent node to the child node to be deleted
3. The node to be deleted has left and right subtrees: replace the deleted node with the smallest element of the right subtree or the largest element of the left subtree
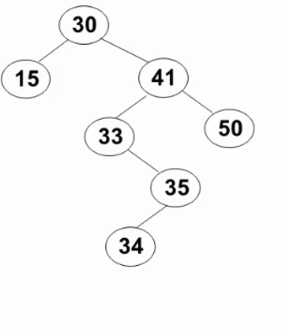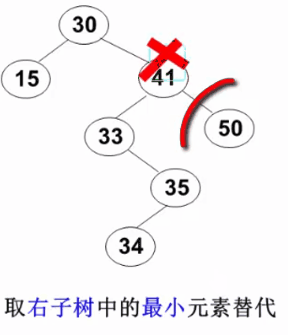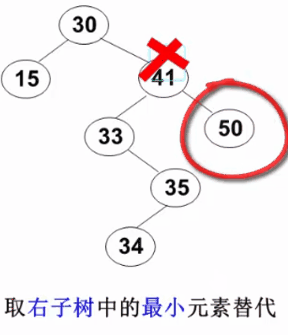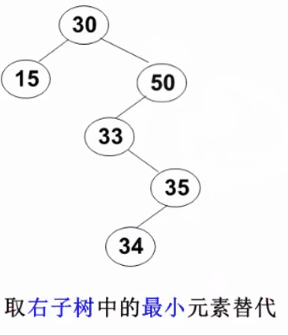
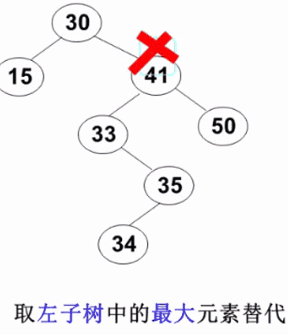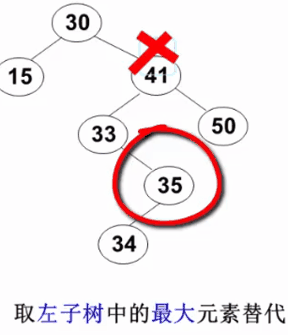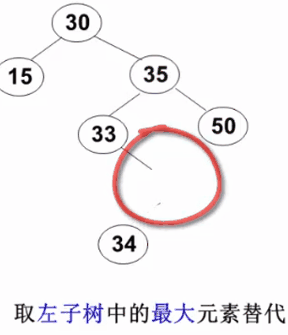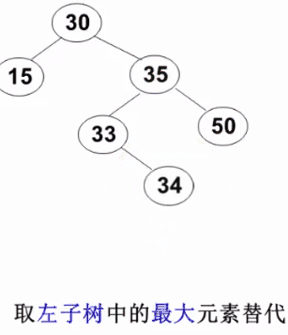
// delete
BinTree Delete(ElementType X,BinTree BST){
BinTree tmp;
if(!BST) //Recursive end flag!!!!!
cout<<"The element to be deleted was not found";
else if(X < BST->Data) // X is smaller than the current node value. Continue to search and delete in the left subtree
BST->Left = Delete(X,BST->Left);
else if(BST->Data < X) // X is larger than the current node value. Continue to search and delete in the right subtree
BST->Right = Delete(X,BST->Right);
else{ // Find the deleted node
if(BST->Left && BST->Right){ // The deleted node has two children
tmp = FindMin(BST->Right); // Find the lowest value in the right subtree
BST->Data = tmp->Data; // Overwrite the current node with the found value
BST->Right = Delete(tmp->Data,BST->Right); // Delete the minimum node of the right subtree found earlier
}else{ // The deleted node has only one child node or no child node
tmp = BST;
if(!BST->Left && !BST->Right) // No child nodes
BST = NULL;
else if(BST->Left && !BST->Right) // Only left child nodes
BST = BST->Left;
else if(!BST->Left && BST->Right) // Only right child nodes
BST = BST->Right;
free(tmp);
}
}
return BST;
}
2.4 insertion
// insert
BinTree Insert(ElementType X,BinTree BST){
if(!BST){ // If it is empty, initialize the node and the end flag!!!!!!!!!!!
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}else{ // Not empty
if(X < BST->Data) // If it's small, hang it on the left
BST->Left = Insert(X,BST->Left);
else if(BST->Data < X) // If it's big, hang it on the right
BST->Right = Insert(X,BST->Right);
// If it's equal, you don't have to do anything
}
return BST;
}
2.5 middle order traversal
// Medium order traversal
void InOrderTraversal(BinTree BT){
if(BT){
InOrderTraversal(BT->Left); // Enter left subtree
cout<<BT->Data; // Print root
InOrderTraversal(BT->Right); // Enter right subtree
}
}
2.6 testing
int main(){
BinTree BST = NULL;
BST = Insert(5,BST);
BST = Insert(7,BST);
BST = Insert(3,BST);
BST = Insert(1,BST);
BST = Insert(2,BST);
BST = Insert(4,BST);
BST = Insert(6,BST);
BST = Insert(8,BST);
BST = Insert(9,BST);
/*
5
/\
3 7
/\ /\
1 4 6 8
\ \
2 9
*/
cout<<"The result of medium order traversal is:";
InOrderTraversal(BST);
cout<<endl;
cout<<"The minimum value to find is:"<<FindMin(BST)->Data<<endl;
cout<<"The maximum search value is:"<<FindMax(BST)->Data<<endl;
cout<<"Find the left subtree of the node with the value of 3. The node value is:"<<Find(3,BST)->Left->Data<<endl;
cout<<"The node value of the right subtree of the node with the lookup value of 7 is:"<<IterFind(7,BST)->Right->Data<<endl;
cout<<"Delete node with value of 5"<<endl;
Delete(5,BST);
/*
6
/\
3 7
/\ \
1 4 8
\ \
2 9
*/
cout<<"The result of medium order traversal is:";
InOrderTraversal(BST);
cout<<endl;
return 0;
}
3. Balanced binary tree
The search efficiency of the binary search tree is related to the depth of the tree, and the composition of the binary search tree is related to its insertion sequence. In extreme cases, the binary search tree degenerates into a single chain (for example, the insertion sequence is 1, 2, 3... n), which greatly reduces the search efficiency. In order to avoid this situation, we use the binary balanced tree to adjust the insertion node, Make the depth of the tree as small as possible.
Balance factor: BF (T) = HL HR, which are the height of left and right subtrees respectively
Balanced binary tree (AVL tree): an empty tree, or a tree in which the absolute value of the height difference between the left and right subtrees of any node does not exceed 1, that is, | BF(T) | ≤ 1
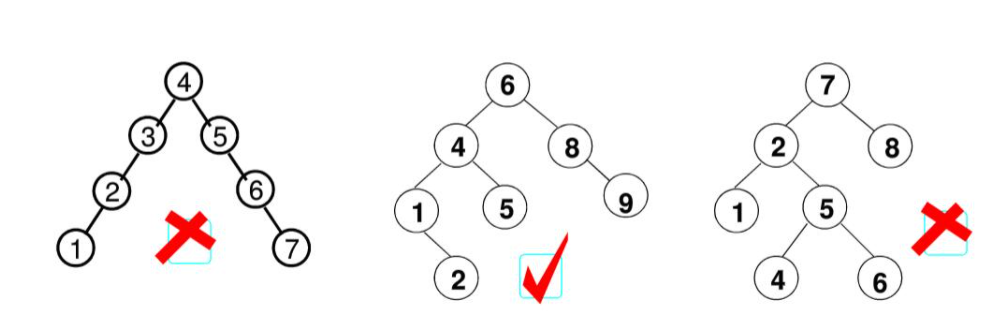
4. Adjustment of balanced binary tree
- follow a principle
Adjust from the node closest to the insertion node
4.1 RR single spin
When the "insert node" (BR) is the right subtree of the right subtree of the "destroyed balance node" (A), that is, RR insertion, RR rotation adjustment is adopted
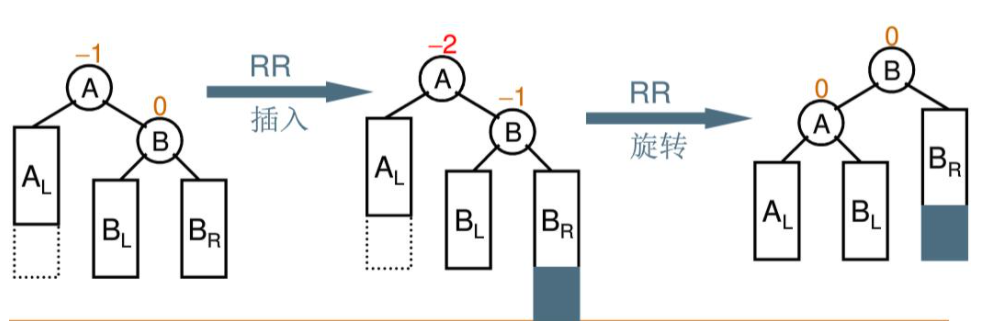
Vacate the left subtree of B and hang it on the right subtree of A, and return B as the root of the current subtree
C
AVLTree RRRotation(AVLTree A){
AVLTree B = A->right; // B is the right subtree of A
A->right = B->left; // The left subtree of B hangs on the right subtree of A
B->left = A; // A hangs on the left subtree of B
return B; // At this point, B is the root node
}
4.2 LL single rotation
When the "insertion node" (BL) is the left subtree of the left subtree of the "destroyed balance node" (A), that is, LL insertion, RR rotation adjustment is adopted
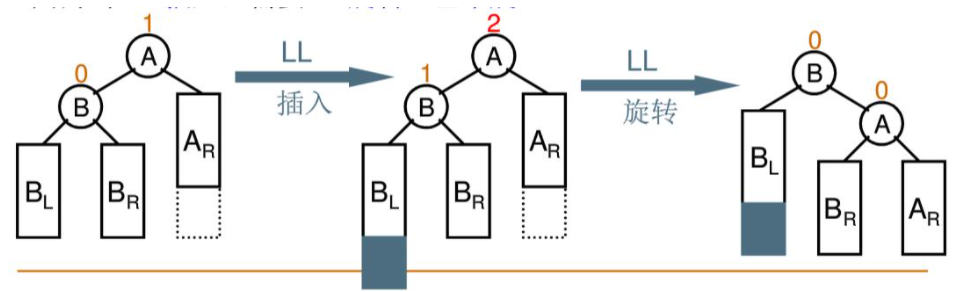
The left subtree is the root of the current subtree B, and the vacated subtree B is returned to the left subtree
c
AVLTree LLRotation(AVLTree A){
// At this time, the root node is A
AVLTree B = A->left; // B is the left subtree of A
A->left = B->right; // The right subtree of B hangs on the left subtree of A
B->right = A; // A hangs on the right subtree of B
return B; // At this point, B is the root node
}
4.3 LR double rotation
When the "insertion node" (CL or CR) is the right subtree of the left subtree of the "destroyed balance node" (A), that is, LR insertion, LR rotation adjustment is adopted
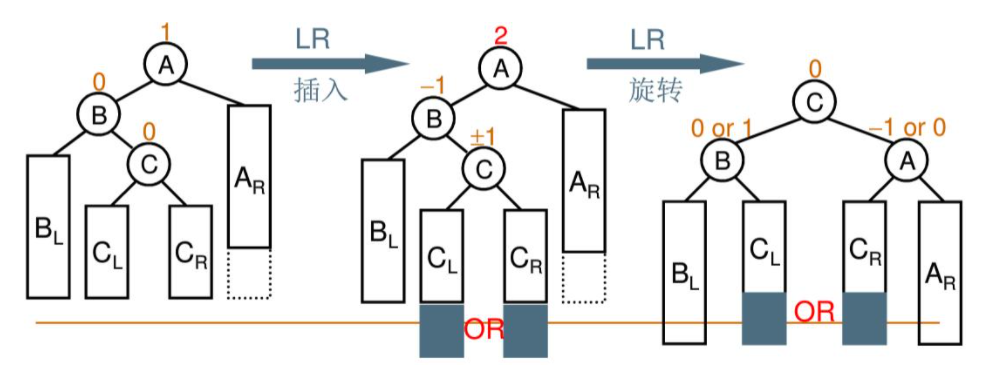
AVLTree LRRotation(AVLTree A){
// First RR single rotation
A->left = RRRotation(A->left);
// Re single rotation
return LLRotation(A);
}
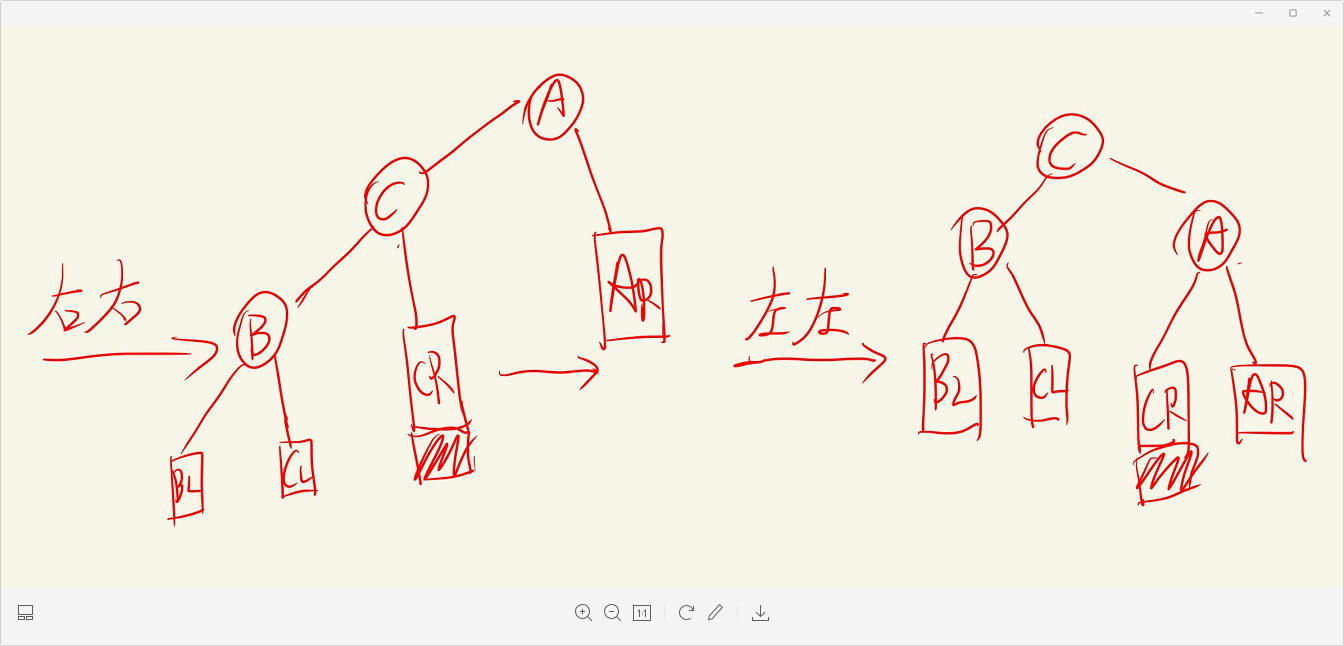
Conclusion: LR double rotation is viewed from top to bottom, while RR single rotation and LL single rotation are actually viewed from bottom to top
4.4 RL double rotation
When the "insert node" (CL or CR) is the left subtree of the right subtree of the "destroyed balance node" (A), that is, RL insertion, RL rotation adjustment is adopted
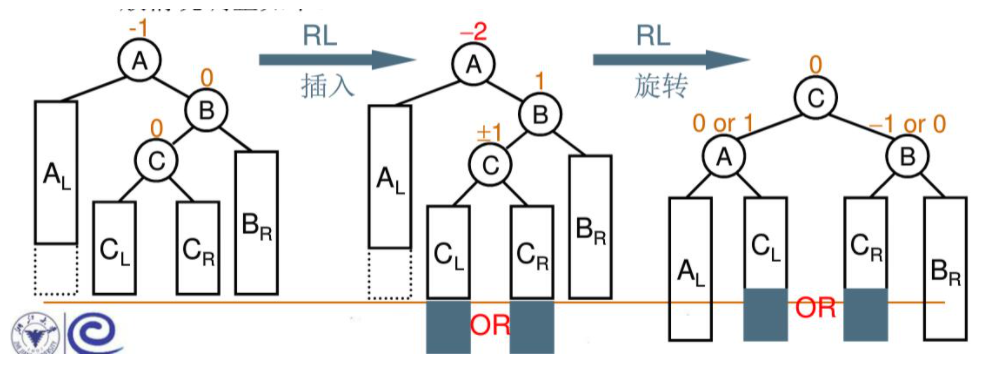
The basic idea is to convert LL single rotation into RR insertion with B as the root node, and then RR single rotation with A as the root node (LL and RR first)
AVLTree RLRotation(AVLTree A){
// First LL single rotation
A->right = LLRotation(A->right);
// Re RR single rotation
return RRRotation(A);
}
Conclusion: RL double rotation is from top to bottom, while the actual first LL single rotation and then RR single rotation is from bottom to top