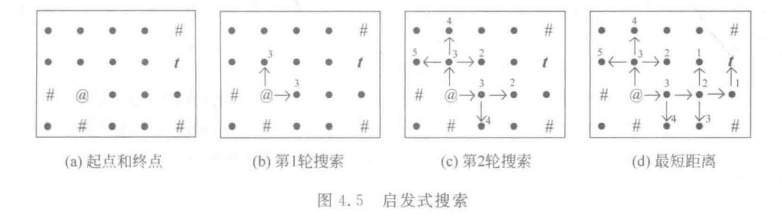
A* search:
Combining BFS and greedy algorithm, it is usually used for game pathfinding. A * is one of the heuristic search algorithms
BFS:
Like ripples, it spreads out circle by circle, but it doesn't care where the end point is
Breadth first, store the starting point in the queue, add the points that have not been visited up, down, left, right to the queue, and list the starting point. To save the state of a node, you can record the state directly with an array or add a state attribute with a structure.
struct Node
{
int x, y;
int state = 0;
};
int dir[4][2] = {
{-1,0},{0,-1},{1,0},{0,1}
};//Lower left and upper right
//int room[9][9]={'.'};
void BFS(int dx, int dy)
{
Node start, next;
queue<Node> q;
start.x = dx;
start.y = dy;
q.push(start);
while (!q.empty())
{
start = q.front();
q.pop();
for (int i = 0; i < 4; i++)
{
next.x = start.x + dir[i][0];
next.y = start.y + dir[i][1];
if (next.x >= 0 && next.x < 9 && next.y >= 0 && next.y < 9&&next.state == 0)
{
next.state = 1;
//room[next.x][next.y]='#';
q.push(next);
}
}
}
}
Greedy algorithm:
As close as possible to the target, but it may fall into local optimization (stuck in the corner). A typical dijestra algorithm (take a shortcut, which must be the shortest path)
Save drawing:
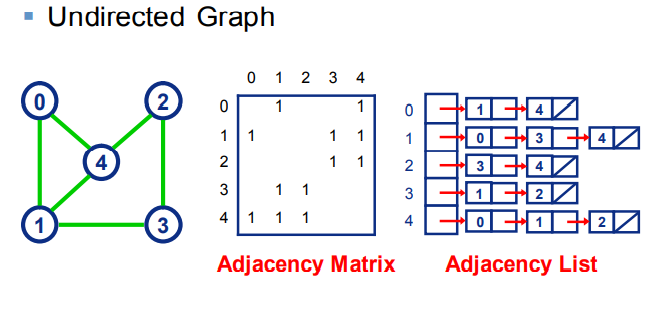
There are two common methods for saving drawings:
Adjacency matrix: set the coordinate value of two points connected by one edge to 1; a[n][n];
Adjacency table: array plus vector, vector < edge > e[n], e[n] stores the edge e[n] connected by each point at(i);
Dijkstra's algorithm
1. Start from the starting point and go to the nearest point every time. (at this time, it is locally optimal, and the nearest point is q.top())
2. Go forward from the nearest point. If it is closer than the starting point, update the shortest distance
(dis[e.v]>dis[u.v]+e.w)
3. Go back to 1 and find the nearest point
4. Until all points are traversed (the queue is empty)

struct edge
{
int to, w;
edge(int a, int b) { to = a; w = b; }
};//Weight (distance) of the other end of the edge and the edge
vector<edge> e[V];
struct s_node {
int v, dis;
s_node(int a, int b) {
v = a; dis = b;
}//A structure built solely for the purpose that the priority queue can discharge the point closest to the starting point
bool operator< (const s_node& a) const
{
return dis < a.dis;
}
};
void dijkstra(int s)
{
int dis[V] = { INF };//The distance from each point except the starting point to the starting point is Inf
bool done[V] = { false };//At first, none of the points were visited
dis[s] = 0;
priority_queue<s_node> q;
q.push(s_node(s, 0));//Put the starting point into the queue
while (!q.empty())
{
s_node u = q.top(); //u is the point closest to the starting point
if(done[u.v]==true)
continue;//Card out the points in the queue that are in the back but have updated the shortest distance in front
q.pop();
done[u.v] = true;//The tag u has been accessed and cannot go back
for (int i = 0; i < e[u.v].size(); i++)//Traverse each edge
{
edge e0 = e[u.v].at(i);//Easy to write at the other end E0 v. Edge weight E0 w
if (done[e0.to] == false && dis[e0.to] > dis[u.v] + e0.w)//Update shortest distance
{
dis[e0.to] = dis[u.v] + e0.w;
q.push(s_node(e0.to, dis[e0.to]));//Join the queue
pre[e0.to]=u0.v //Record path
}
}
}
}A * algorithm
The expansion of dijestra algorithm knows where the end point is and will not blindly search in breadth.
Differences: greedy from the shortest path to the evaluation function f=g+h; The others are as like as two peas.
g is the distance from the starting point to the current square; h is the distance from the end point to the box (ignoring obstacles). Generally, it is Manhattan distance (horizontal distance plus vertical distance). The distance of walking obliquely is 1.414 times that of walking horizontally.
The code is implemented in resources
reference material:
Introduction to the a * algorithm (redblobnames. Com)
Teacher's ppt, algorithm book