Question 1:
You are a professional thief who plans to steal houses along the street. There is a certain amount of cash hidden in each room. The only restrictive factor affecting your theft is that the adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.
Given an array of non negative integers representing the amount stored in each house, calculate the maximum amount you can steal overnight without touching the alarm device.
Example 1:
Input: [1,2,3,1] Output: 4 Explanation: steal house 1 (amount = 1) and then steal house 3 (amount = 3). Maximum amount stolen = 1 + 3 = 4.
Example 2:
Input: [2,7,9,3,1] Output: 12 Explanation: steal house 1 (amount = 2), steal house 3 (amount = 9), and then steal house 5 (amount = 1). Maximum amount stolen = 2 + 9 + 1 = 12.
Tips:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 400
1 class Solution { 2 public int rob(int[] nums) { 3 //dp[i] dp[i-1] perhaps dp[i-2]+nums[i] 4 int n=nums.length; 5 int[] dp=new int[n+2]; 6 for (int i=2;i<n+2;i++) { 7 dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i-2]); 8 } 9 return dp[n+1]; 10 } 11 }
Idea: dp[i] refers to the maximum money obtained by 0~i family. dp[i] depends on dp[i-1], that is, if i-1 family is stolen, I-I family cannot steal, or if i-2 family is stolen, dp[i-2] + steal today. In order to avoid array overflow, two more arrays are opened.
Question 2:
You are a professional thief. You plan to steal houses along the street. There is a certain amount of cash in each room. All the houses in this place are} enclosed in a circle, which means that the first house and the last house are next to each other. At the same time, adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.
Given an array of nonnegative integers representing the amount stored in each house, calculate the maximum amount you can steal tonight without touching the alarm device.
Example 1:
Input: num = [2,3,2] Output: 3 Explanation: you can't steal house 1 (amount = 2) and then house 3 (amount = 2) because they are adjacent.
Example 2:
Input: num = [1,2,3,1] Output: 4 Explanation: you can steal house 1 (amount = 1) and then house 3 (amount = 3). Maximum amount stolen = 1 + 3 = 4.
Example 3:
Input: num = [1,2,3] Output: 3
Tips:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 1000
1 class Solution { 2 public int rob(int[] nums) { 3 // In the first case, you must steal the first one. Start with the third one dp reach n-1 4 // In the second case, we must not steal the first one, but start from the second one dp reach n 5 int n=nums.length,ans=0; 6 int[] dp=new int[n+2]; 7 //First case 8 for (int i=4;i<n+2;i++) { 9 dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i-2]); 10 } 11 ans=Math.max(ans,dp[n]+nums[0]); 12 Arrays.fill(dp,0); 13 //The second case 14 for (int i=3;i<n+2;i++) { 15 dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i-2]); 16 } 17 return Math.max(dp[n+1],ans); 18 } 19 }
Idea: considering that the first choice affects the last choice, first judge the situation of the first one, and then dp
Question 3:
The thief found a new area that could be stolen. There is only one entrance in this area, which we call "root".
Except for the "root", each house has and only has a "parent" house connected to it. After some reconnaissance, the smart thief realized that "the arrangement of all houses in this place is similar to a binary tree". If two directly connected houses are robbed on the same night, the house will automatically call the police.
The root of a given binary tree. Returns the maximum amount a thief can steal without triggering the alarm.
Example 1:
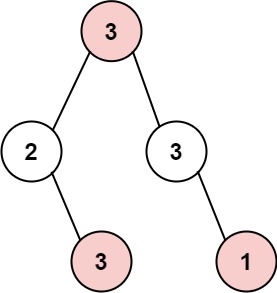
Input: root = [3,2,3,null,3,null,1] Output: 7 Explanation: the maximum amount a thief can steal in one night is 3 + 3 + 1 = 7
Example 2:
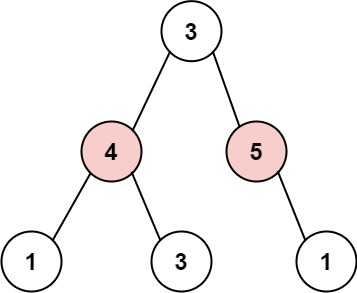
Input: root = [3,4,5,1,3,null,1] Output: 9 Explanation: the maximum amount a thief can steal in one night is 4 + 5 = 9
Tips:
- The number of nodes in the tree is in the range of [1, 104]
- 0 <= Node.val <= 104
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 Map<TreeNode, Integer> f = new HashMap<TreeNode, Integer>(); 18 Map<TreeNode, Integer> g = new HashMap<TreeNode, Integer>(); 19 20 public int rob(TreeNode root) { 21 dfs(root); 22 return Math.max(f.getOrDefault(root, 0), g.getOrDefault(root, 0)); 23 } 24 25 public void dfs(TreeNode node) { 26 if (node == null) { 27 return; 28 } 29 dfs(node.left); 30 dfs(node.right); 31 f.put(node, node.val + g.getOrDefault(node.left, 0) + g.getOrDefault(node.right, 0)); 32 g.put(node, Math.max(f.getOrDefault(node.left, 0), g.getOrDefault(node.left, 0)) + Math.max(f.getOrDefault(node.right, 0), g.getOrDefault(node.right, 0))); 33 } 34 }
Idea: use hash table records to dynamically plan. Each node has two choices. Let f function be choice and G be no choice. If f(root) =g(left)+g(right), if not, g(root)=max(f(left),g(left))+max(f(right)+g(right)). Depth traversal, and finally return the larger one.