Alice and Bob are playing games with some stones. There are even piles of stones in a row; There are ， integer stones in each pile, and the number is ， pieces [i].

The game is decided by who has the most stones in his hand. The total number of stones is odd, so there is no draw.

Alice and Bob take turns. Alice starts first. In each turn, the player takes the whole pile of stones from the beginning or end of the line. This situation continues until there are no more stone piles. At this time, the player with the most stones wins.

Assuming that both Alice and Bob play their best, Alice returns true when she wins the game, and Bob returns false when he wins the game.

Example 1:

Input: piles = [5,3,4,5]
Output: true
 Explanation:
Alice starts first and can only take the first five or the last five stones.
If he takes the first five, this line becomes [3,4,5].
If Bob takes the first three, the rest is [4,5]. Alice takes the last five and wins 10 points.
If Bob takes the last five, the rest is [3,4]. Alice takes the last four and wins 9 points.
This shows that taking the first five stones is a victory for Alice, so it returns true.

Example 2:

Input: piles = [3,7,2,3]
Output: true

Tips:

• 2 <= piles.length <= 500
• piles.length is an even number
• 1 <= piles[i] <= 500
• sum(piles[i]) is an odd number

 1 class Solution {
 2     public boolean stoneGame(int[] piles) {
 3         int n=piles.length;
 4         Result[][] dp=new Result[n][n];
 5         //section dp
 6         //dp[i][j]express i~j The result of the pile, fir Is the biggest pioneer, sec It's the biggest backhand
 7         for (int i=0;i<n;i++){
 8             for (int j=i;j<n;j++){
 9                 dp[i][j]=new Result(0,0);
10             }
11         }
12         //boundary condition 
13         for (int i=0;i<n;i++) {
14             dp[i][i].fir=piles[i];
15             dp[i][i].sec=0;
16         }
17         // Traverse obliquely and inversely
18         for (int i=n-2;i>=0;i--) {
19             for (int j=i+1;j<n;j++) {
20                 // Select the left and right results first
21                 int left=dp[i+1][j].sec+piles[i];
22                 int right=dp[i][j-1].sec+piles[j];
23                 if (left>right) {
24                     dp[i][j].fir=left;
25                     dp[i][j].sec=dp[i+1][j].fir;
26                 }else {
27                     dp[i][j].fir=right;
28                     dp[i][j].sec=dp[i][j-1].fir;
29                 }
30             }
31         }
32         return dp[0][n-1].fir>dp[0][n-1].sec;
33     }
34 }
35 
36 class Result{
37     int fir;
38     int sec;
39     //fir First hand
40     //sec Indicates a backhand
41     Result(int fir,int sec){
42         this.fir=fir;
43         this.sec=sec;
44     }
45 }

Ideas: general dynamic planning ideas, such as notes.

Question 2:

Given a # m # x # n # grid containing non negative integers, please find a path from the upper left corner to the lower right corner so that the sum of numbers on the path is the smallest.

Note: you can only move down or right one step at a time.

 

Example 1:

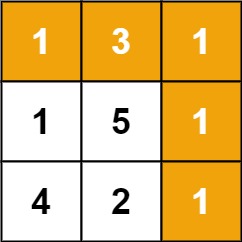
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
 Explanation: because the sum of paths 1 → 3 → 1 → 1 → 1 is the smallest.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

 

Tips:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

 1 class Solution {
 2     public int minPathSum(int[][] grid) {
 3         int m=grid.length,n=grid[0].length;
 4         int[][] dp=new int[m+1][n+1];
 5         for (int i=0;i<=m;i++) Arrays.fill(dp[i],Integer.MAX_VALUE);
 6         dp[0][1]=0;
 7         dp[1][0]=0;
 8         for (int i=1;i<=m;i++) {
 9             for (int j=1;j<=n;j++) {
10                 dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
11             }
12         }
13         return dp[m][n];
14     }
15 }

Idea: dp[i][j] indicates the minimum value of I-1 and J-1 coordinates. In order to prevent the array from crossing the boundary, open one more row and one more column array. For boundary conditions, let dp[1][1] be grid[0][0], let dp[1][0] or dp[0][1] take 0, and the other initial values take the maximum value.