Examples
1. Stock trading
Title Description
Given an array with length N, the ith number in the array represents the price of a given stock on day i.
Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buying and selling a stock multiple times).
Note: you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).
Input format
The first line contains the integer N, which represents the length of the array.
The second line contains N positive integers no greater than 10000, representing the complete array.
Output format
Output an integer representing the maximum profit.
Data range
1≤N≤105
Input example 1:
6
7 1 5 3 6 4
Output example 1:
7
Input example 2:
5
1 2 3 4 5
Output example 2:
4
Input example 3:
5
7 6 4 3 1
Output example 3:
0
Example explanation
Example 1: buy on the second day (stock price = 1) and sell on the third day (stock price = 5). This exchange can make a profit = 5-1 = 4. Then, buy on the 4th day (stock price = 3) and sell on the 5th day (stock price = 6). This exchange can make a profit = 6-3 = 3. Total profit 4 + 3 = 7.
Example 2: buy on the first day (stock price = 1) and sell on the fifth day (stock price = 5). This exchange can make a profit = 5-1 = 4. Note that you can't buy stocks on day 1 and day 2 and then sell them. Because this is involved in multiple transactions at the same time, you must sell the previous shares before buying again.
Example 3: in this case, no transaction is made, so the maximum profit is 0.
Problem solving ideas
Seeing this problem, I thought of the problem I did in LeetCode The best time to buy stocks The difference is that stock trading can be traded many times. We can choose to sell or buy at any time as long as the final profit is the largest. The greed of this topic is: as long as the price in front is less than the price in the back at two adjacent times, we will trade once. It must be that selling at a higher price will make a profit, but if we only buy at the lowest price, selling at the highest price is not necessarily the maximum profit. For example, example 1, because we can also trade before or after that.
Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
const int N=100010;
int p[N];
int n;
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>p[i];
int res=0;
for(int i=0;i<n-1;i++)
{
int dt=p[i+1]-p[i];
if(dt>0) res+=dt;
}
cout<<res<<endl;
return 0;
}
2. Warehouse location
Title Description
There are N stores on a number axis, and their coordinates are A1 ∼ AN respectively.
Now we need to build a warehouse on the number axis. Every morning, a truck of goods will be transported from the warehouse to each store.
In order to improve efficiency, where to build the warehouse can minimize the sum of the distance from the warehouse to each store.
Input format
Enter the integer N on the first line.
The second line contains N integers A1 ∼ AN.
Output format
Output an integer representing the minimum value of the sum of distances.
Data range
1≤N≤100000,
0≤Ai≤40000
Input sample:
4
6 2 9 1
Output example:
12
Problem solving ideas
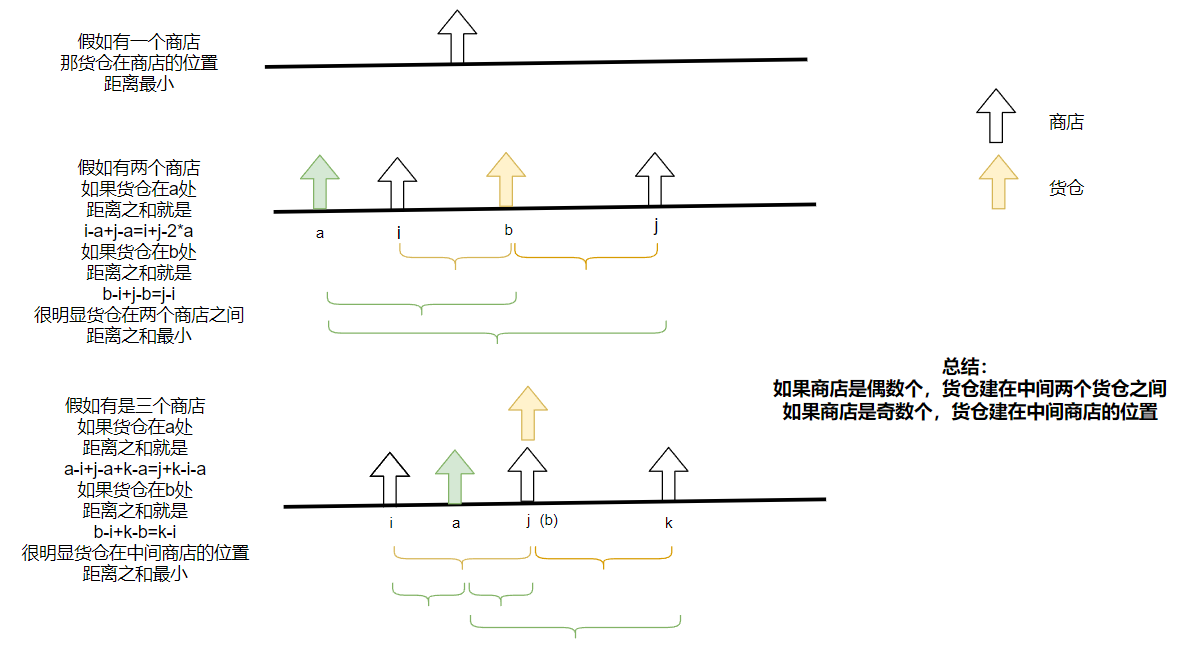
Mathematical proof:

Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010;
int a[N];
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n);//Sort all stores by location
int res=0;
for(int i=0;i<n;i++) res+=abs(a[i]-a[n/2]);//n/2 is the warehouse in the middle of all stores. If n is an even number, take the one on the left of the middle two. If n is an odd number, it is the middle one
cout<<res<<endl;
}
3. Candy delivery
Title Description
There are n children sitting in a circle, each with a[i] a candy.
Each person can only pass candy to the left and right.
Each person passes one candy at a time at a cost of 1.
The minimum cost of making candy equal to everyone.
Input format
In the first line, enter a positive integer n, indicating the number of children.
Next, there are n lines, with an integer a[i] in each line, indicating the number of candy initially obtained by the ith child.
Output format
Output an integer representing the minimum cost.
Data range
1≤n≤1000000,
0≤a[i]≤2×109,
The data guarantee must have a solution.
Input sample:
4
1
2
5
4
Output example:
4
Problem solving ideas
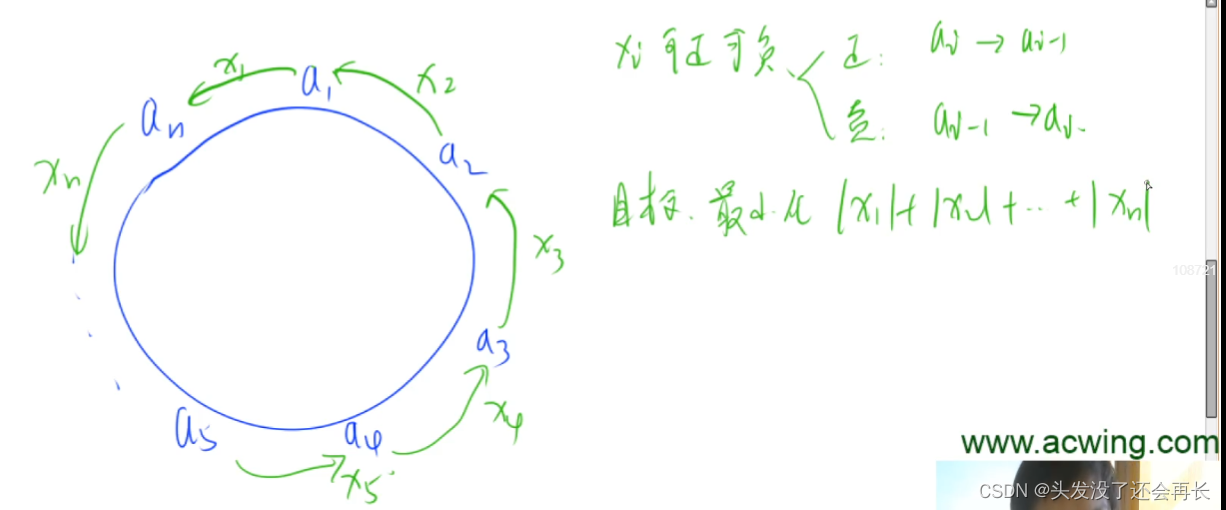

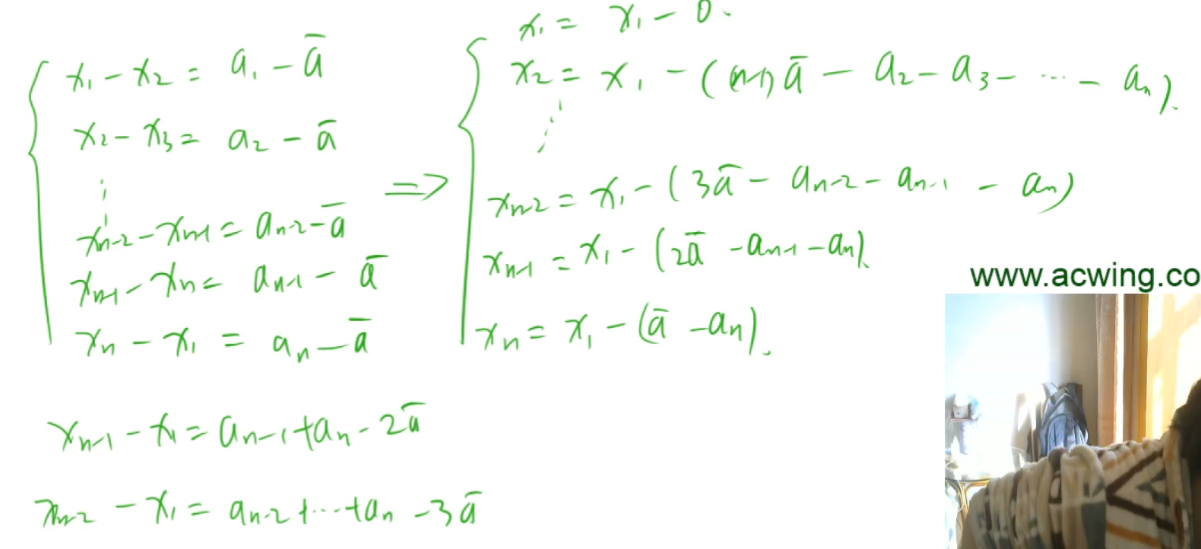
After the transformation, this question is the same as the last one
 >
>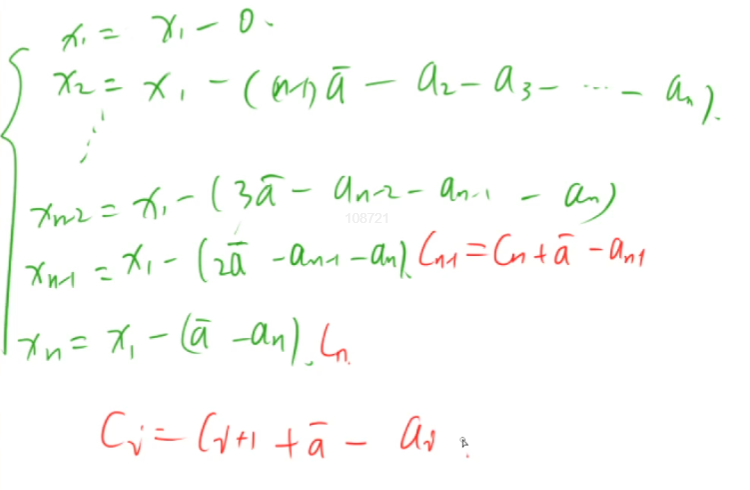
Therefore, first calculate the C array from the A array with the formula. After obtaining the C array, find A point as the same as the previous question, so as to minimize the sum of the distance from this point to all points of the C array
Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1000010;
typedef long long LL;
int a[N];
LL c[N];
LL sum;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) sum+=a[i];
int ave=sum/n;//Find the average number of sweets
for(int i=n;i>1;i--) c[i]=c[i+1]+ave-a[i];//Seek C
c[1]=0;
sort(c+1,c+n+1);
LL res=0;
for(int i=1;i<=n;i++) res+=abs(c[i]-c[(i+1)/2]);//Find the minimum value of the sum of all distances through C
cout<<res<<endl;
return 0;
}
4. Radar equipment
Title Description
Suppose the coast is an infinite straight line, the land is on one side of the coast and the ocean is on the other side.
Each island is located at a point on the ocean side.
All radar devices are located on the coastline, and the monitoring range of the radar is d. when the distance between the island and a radar does not exceed D, the island can be covered by the radar.
We use the Cartesian coordinate system to define the coastline as the x-axis, with the sea side above the x-axis and the land side below the x-axis.
Now give the specific coordinates of each island and the detection range of the radar. Please find out the minimum number of radars required to make all islands covered by the radar.
Input format
In the first line, enter two integers n and d, representing the number of islands and radar detection range respectively.
Next, enter two integers in n lines, representing the x and y axis coordinates of the island.
The same row of data is separated by spaces.
Output format
Output an integer representing the minimum number of radars required. If there is no solution, the required number is output − 1.
Data range
1≤n≤1000,
−1000≤x,y≤1000
Input sample:
3 2
1 2
-3 1
2 1
Output example:
2
Problem solving ideas
It does not consider how many ranges each radar can cover, but how many radar ranges each island can cover. As long as there is radar in the range of each island, the island can be covered. Therefore, for all islands, there must be at least one radar in all ranges
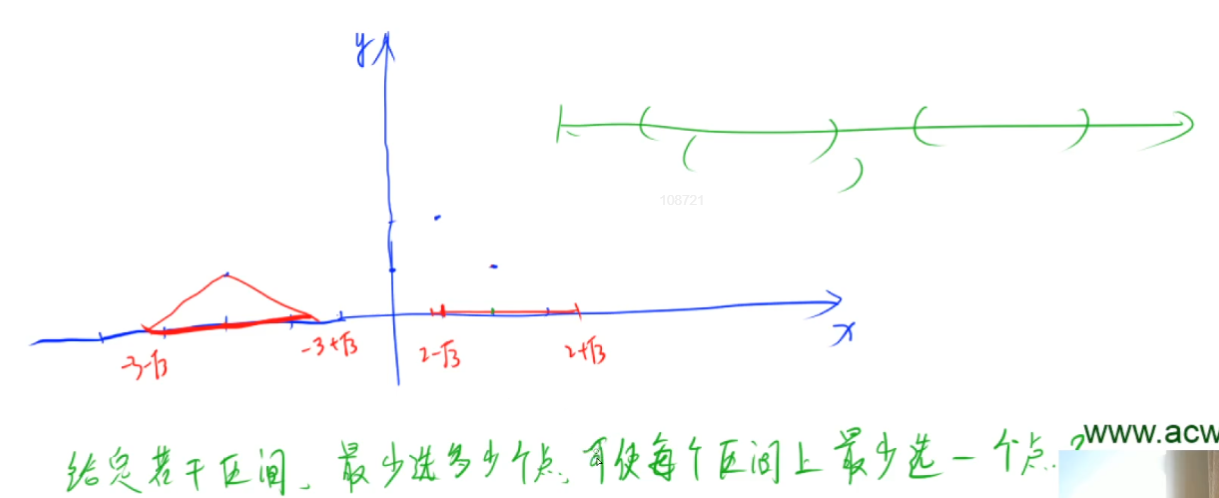


Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=1010;
int n,d;
struct Segment{
double l,r;
bool operator< (const struct Segment& t)const{
return r<t.r;
}
}seg[N];
int main()
{
cin>>n>>d;
bool failed=false;
for(int i=0;i<n;i++)
{
int x,y;
cin>>x>>y;
if(y>d) failed=true;//The straight-line distance is the shortest. If the shortest distance is greater than d, it means that the radar cannot detect it
else{
double len=sqrt(d*d-y*y);
seg[i].l=x-len,seg[i].r=x+len;//The range that can be detected by radar of the island
}
}
if(failed) cout<<-1<<endl;
else{//How many radars are needed
sort(seg,seg+n);
int cnt=0;
double last=-1e20;
for(int i=0;i<n;i++)
{
if(seg[i].l>last)//If the section is not detected by the last radar, add a radar
{
cnt++;
last=seg[i].r;//The position of the radar is the right end point of the section
}
}
cout<<cnt<<endl;
}
return 0;
}
Blue Bridge Cup
1. Payment problem
Title Description
It is common for several people to go out to dinner together.
But when checking out, there are often some disputes.
Now there are n people going out to eat. They spent S yuan in total.
Among them, the i-th person brought ai yuan.
Fortunately, the total amount of money everyone brings is enough to pay the bill, but now the question comes: how much does each person pay?
For the sake of fairness, we hope that under the premise that the total payment is just S, the standard deviation of each person'S payment will be the smallest.
Here we agree that the amount of money paid by each person can be any non negative real number, that is, it can not be an integral multiple of a penny.
What is the minimum standard deviation you need to output.
Introduction to standard deviation: standard deviation is the square average of the difference between multiple numbers and their average. It is generally used to describe the "how big the deviation is" between these numbers.
Formally speaking, let the i-th person pay bi Yuan, then the standard deviation is:
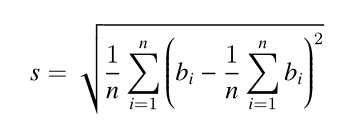
Input format
The first line contains two integers n, S;
The second line contains n non negative integers a1, ..., an.
Output format
Output the minimum standard deviation, round to 4 decimal places.
Data range
1≤n≤5×10^5,
0≤ai,S≤10^9
Input example 1:
5 2333
666 666 666 666 666
Output example 1:
0.0000
Input example 2:
10 30
2 1 4 7 4 8 3 6 4 7
Output example 2:
0.7928
Problem solving ideas

Prove the establishment of greed
1. When AI > = (s / N), take bi=s/n as the minimum, and take (bi-s/n) as xi, which is proved as follows:

2. When ai < s / N, take bi=ai as the minimum. If bi 'is less than ai, then there must be a BJ > s / N (because bi < s / N, if the sum is equal to s, there must be a person whose contribution is greater than n/s, then the sum can be equal to s)
Next, we will prove when the equation with the sum of two squares takes the maximum
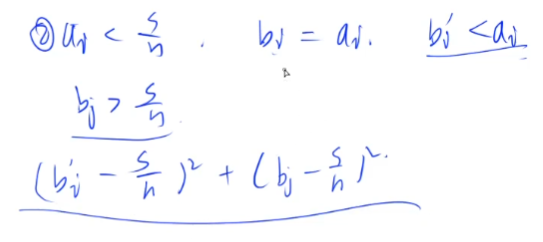
The certificate is as follows:
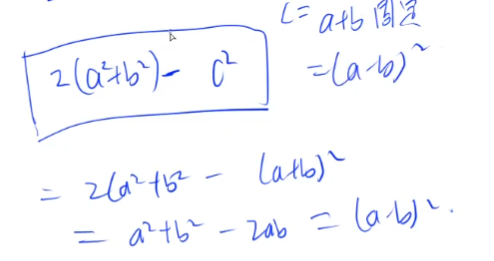
Therefore, when the difference between two numbers is the smallest and the sum of squares of the two numbers is the smallest, then the difference between bi 'and bj should be the smallest, that is, bi' should be larger and bj should be smaller, so bi 'should be ai, so bj will also be smaller (for example, I only have 2 yuan and the other person has 5 yuan. We should have paid 6 yuan, that is, each person pays 3 yuan, but I only pay 1 (bi') yuan, If another person wants to pay 4 (bj), our difference will be very large, but if I pay 2 (bi ') yuan and another person pays 3 (bj), our difference will be smaller)
Method: sort the amount of money everyone brings, starting from A1. If A1 < n / s, the first person only needs to pay A1 yuan, and the rest will pay s-a1. The second person should pay (s-a1)/(n-1). If a2 < (s-a1)/(n-1), the second person only needs to pay a2 yuan. If it is greater than or equal to (s-a1)/(n-1), and so on. Why do you want to sort? Because if the people in front don't have enough money, the people in the back can make up for more money, but if the people in front have more money, they only pay s/n, and the people in the back can't make up for less money
Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int N=500010;
int a[N];
typedef long long LL;
int main()
{
int n;
double s;
cin>>n>>s;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n);
double ave=s/n,res=0;//They are the mean value of everyone's money and the sum of squares of all numbers
for(int i=0;i<n;i++)
{
double cur=s/(n-i);//The money that i should pay
if(a[i]<cur) cur=a[i];//If not, give a[i]
res+=(cur-ave)*(cur-ave);//Cumulative sum of squares
s-=cur;//The remaining total amount of money to be paid is deducted from the amount of money already paid each time
}
printf("%.4lf",sqrt(res/n));//standard deviation
return 0;
}
2. Maximum product
Title Description
Give N integers A1,A2,... AN.
Please choose K numbers from them to maximize their product.
Please find the maximum product. Since the product may exceed the integer range, you only need to output the remainder of the product divided by 100000009.
Note that if x < 0, we define that the remainder of X divided by 100000009 is the remainder of negative (− X) divided by 100000009, that is: 0 − ((0 − X)% 100000009)
Input format
The first line contains two integers N and K.
The following N lines each contain an integer Ai.
Output format
Output an integer representing the answer.
Data range
1≤K≤N≤10^5,
−105≤Ai≤10^5
Input example 1:
5 3
-100000
-10000
2
100000
10000
Output example 1:
999100009
Input example 2:
5 3
-100000
-100000
-2
-100000
-100000
Output example 2:
-999999829
Problem solving ideas

After sorting all numbers, the number with the largest absolute value of negative number is on the left, and the number with the largest positive number is on the right. If you want to select odd numbers, first select the rightmost number, point to the leftmost and rightmost of the number to be selected with two pointers respectively, multiply two numbers from the left each time, then multiply two numbers from the right, compare the two products, select the larger one, and then move the pointer, Until k numbers are selected, if it is an even number, select directly one-to-one.
Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=100010,mod=1000000009;
typedef long long LL;
int a[N];
int n,k;
int main()
{
cin>>n>>k;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n);
int res=1;
int l=0,r=n-1;
int sign=1;//When the mark is all negative
if(k%2)//If it is an odd number, take the last one first
{
res=a[r--];
k--;
if(res<0) sign=-1;//If the last one is also negative, mark it
}
while(k)
{
LL x=(LL)a[l]*a[l+1],y=(LL)a[r-1]*a[r];//Multiply two from the left and two from the right
if(x*sign>y*sign)//If sign=-1, it means that all numbers are negative, and the smallest number is removed
{
res=x%mod*res%mod;
l+=2;//Move pointer
}
else
{
res=y%mod*res%mod;
r-=2;
}
k-=2;
}
cout<<res<<endl;
return 0;
}
3. Suffix expression
Title Description
Given n plus signs, M minus signs and N+M+1 integers A1,A2, ⋅⋅⋅, AN+M+1, Xiao Ming wants to know which of all the legal suffix expressions rounded up by N plus signs, M minus signs and N+M+1 integers has the largest result?
Please output this maximum result.
For example, if 123 + − is used, the result of the suffix expression "23 + 1 −" is 4, which is the largest.
Input format
The first line contains two integers N and M.
The second line contains N+M+1 integers A1,A2, ⋅ ⋅, AN+M+1.
Output format
Output an integer representing the answer.
Data range
0≤N,M≤10^5,
−109≤Ai≤10^9
Input sample:
1 1
1 2 3
Output example:
4
Problem solving ideas
The suffix expression is realized by means of a stack. A stack is used to store the number. When an operation symbol is encountered, the two elements at the top of the stack are out of the stack for operation, and the result is put back into the stack.
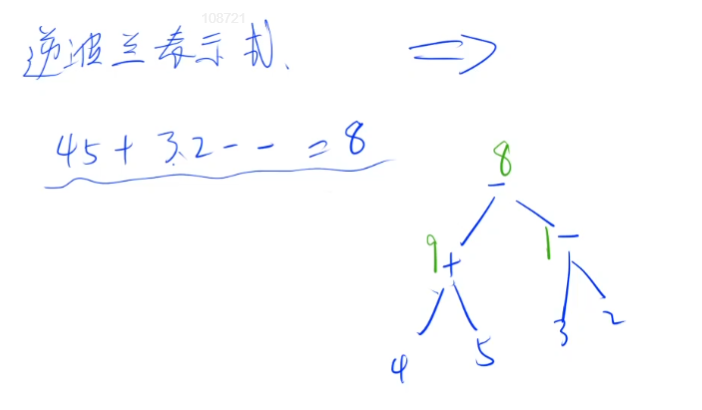
The suffix expression can also be transformed into a binary tree. The countable post order traversal is the expression suffix expression, as follows:
If you want to maximize the value of N+M+1 numbers after addition and subtraction, the intuitive idea is to subtract all negative numbers and add all positive numbers. However, since the minus sign and plus sign are fixed, you should try to subtract more negative numbers. If the negative number is not enough, subtract small positive numbers. b1-(a1-a2-a3-a4)=b1-a1+a2+a3+a4, then 1~M negative numbers can be rounded up to only one negative number, that is, any 1~M negative numbers can be rounded up. If there are n positive numbers, positive numbers can also be rounded up to negative numbers. You can round up any 1~N+M negative numbers
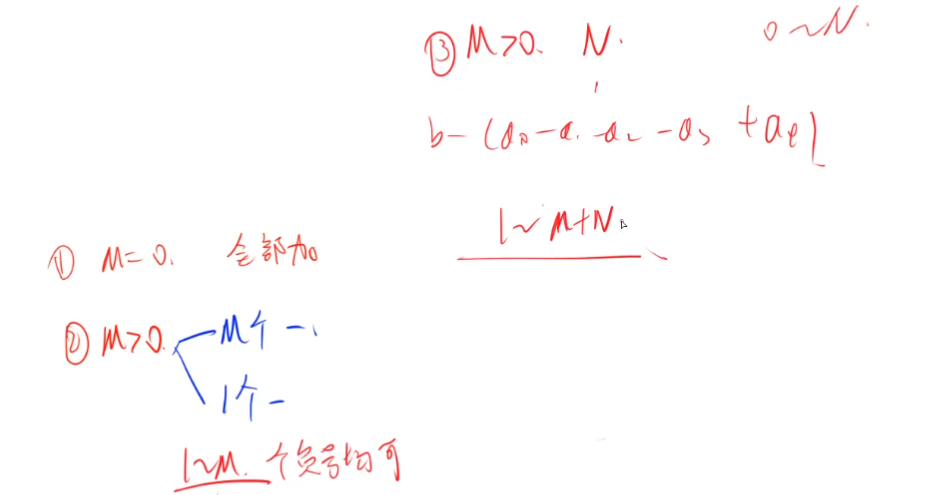
Therefore, if there is a minus sign, no matter how you do it, there must be a minus sign. If you want to make the subtraction larger, there must be a minimum value (the absolute value in the negative number is the largest), and the remaining addition must add the maximum value as much as possible
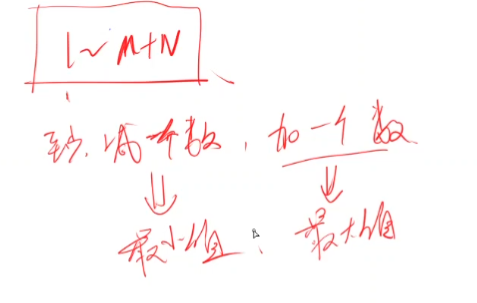
Practice: if M < 0, there is no minus sign, so the sum of all numbers is the maximum value. If there is a minus sign, use the maximum value minus the minimum value plus the absolute value of the remaining numbers. Because as long as the expression has a minus sign, the remaining minus signs can be converted into a plus sign.
Code implementation + detailed notes C++
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=200010;
typedef long long LL;
int a[N];
int n,m;
LL res;
int main()
{
cin>>n>>m;
int k=n+m+1;
for(int i=0;i<k;i++) cin>>a[i];
if(m==0)//If there is no negative number, the value is the sum of all the numbers
{
for(int i=0;i<k;i++) res+=a[i];
}
else
{
sort(a,a+k);
res+=a[k-1]-a[0];//Subtract the minimum from the maximum. The minimum is a negative number
for(int i=1;i<k-1;i++) res+=abs(a[i]);//Then other subtractions are converted into addition. Subtracting all negative numbers is to add the absolute values of all negative numbers
}
cout<<res<<endl;
return 0;
}
summary
It's really hard to prove greed. Do you have time to prove it in the exam? All, guess? hhh, do more questions and sum up experience, come on!!
Learning website: AcWing