Overall summary
This time, it's still in a hurry. One important reason is to prepare for the final exam. I haven't been in touch with the game for a long time. On the whole, we should be familiar with the process and skills of doing questions as soon as possible. Of course, it is more important to improve our ability.
Topic D
The description of the problem is very simple. It looks like a construction problem. In fact, it is more like a mathematical problem. After calculating the relationship between the ratio in this problem, we will find that this problem is actually a problem to solve. According to the form of the solution, we need to see when the solution can meet the conditions, that is, after some roots in the root sign are opened, it can become a rational number. If it is an irrational number, we can directly output 0 0. In this case, we can easily think that there is no integer solution.
code
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <stdlib.h>
#include <stdio.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int maxn = 1e5+10;
const int mod = 1e9+7;
ll gcd(ll a,ll b)
{
if(a<b)
swap(a,b);
ll yu;
yu=a%b;
while(true)
{
a=b;
b=yu;
if(yu==0)
break;
yu=a%b;
}
return a;
}
void solve()
{
bool bol=true;
ll p,q;
scanf("%lld%lld",&p,&q);
ll k=p*p-4*q*q;
ll kk=sqrt(k);
if(kk*kk==k)
bol=true;
else
bol=false;
ll gcdd=gcd(p-kk,q*2);
if(!bol)
printf("0 0\n");
else
{
printf("%lld %lld\n",(p-kk)/gcdd,q*2/gcdd);
}
//printf("%lld %lld\n",1ll*((p-kk)/q)/2,1ll*((p+kk)/q)/2);
}
int main()
{
int t = 1;
scanf("%d",&t);
while(t--)
{
solve();
}
return 0;
}
Title E
My teammates have done this problem. I won't say more here. It's also a sign in problem. Please attach the following link and refer to it.
link
Topic G
I didn't think of this problem when I wrote it. I felt that my sensitivity to the problem was somewhat reduced. At that time, I mentioned that the problem may be a tree dp, but I felt that I couldn't find its optimal substructure, and the idea was very unclear. After seeing other people's solutions, I feel that there are too many things to fill. Here I'd better learn other people's ideas and write it down.
For a tree with n (odd) points, n − 1 edges are divided into n − 12 groups, with two edges in each group, and the two edges must have a common point. Ask the number of grouping schemes. If there are even points in subtree x, the odd edges must not be grouped, and X needs to be connected to its father's edge. If there are an odd number of points, even edges can be grouped.
Let d[x] be the number of schemes for grouping the edges in the subtree of X. let a y of child y of X need (x,y) this edge to be paired with the edge in the subtree of Y, and b y are paired with (x,y) here. Then when B is odd, we also need the edge connected by X to its father. That is, X has an even number of a subtree points and an odd number of B subtree points. Now we only need to consider grouping B subtrees in pairs. If B is odd, then (x,fa) needs to be added.
N elements, two in each group. The number of schemes divided into n2 groups is f[n], and there is a recursive formula f[n]=f[n − 2] * (n − 1).
So:
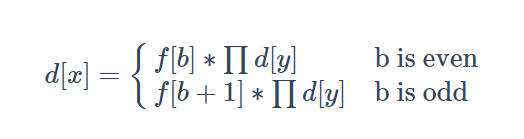
The number of schemes of each subtree is still independent, so the cumulative contribution is still multiplied, but b of them is in order, and the order number is f.
code
#include <bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
typedef long long ll;
const int N = 100010, mod = 998244353;
int n, sz[N];
vector<int> g[N];
ll d[N], f[N];
void dfs(int x, int fa)
{
sz[x] = 1;
d[x] = 1;
int cnt = 0;
for(auto &y : g[x])
{
if(y == fa) continue;
dfs(y, x);
sz[x] += sz[y];
d[x] = d[x] * d[y] % mod;
if(sz[y] & 1) cnt ++;
}
if(cnt & 1) cnt ++;
d[x] = d[x] * f[cnt] % mod;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<n; i++)
{
int x, y;
scanf("%d%d", &x, &y);
g[x].push_back(y);
g[y].push_back(x);
}
f[0] = 1;
for(int i=2; i<=n; i+=2)
{
f[i] = f[i-2] * (i-1) % mod;
}
dfs(3, 0);//In fact, any node can be used as the root node. In fact, it is also possible to traverse with other nodes as the root node
printf("%lld\n", d[3]);
return 0;
}
Topic I
The key to this question is actually what is regarded as the backpack volume. After analysis, we can regard the difference between the two groups of points as the backpack volume. Then, after analyzing the problem, we will find that a card can only be placed in the first or second set instead of repeatedly, It's just that when we put it into the second set, we need to consider whether to double its serial number, so our thinking actually revolves around this point, and we can write it naturally after we think about it. The transfer equation is basically the following case. i is the number of cards, j is the number of times it has doubled, and w is the value of S-T (shifted to the right)
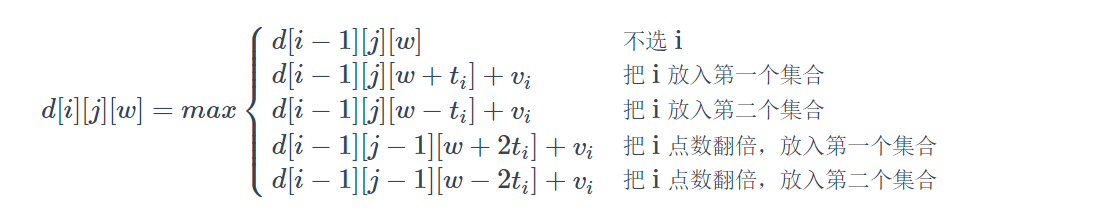
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,s,dp[101][101][5201],v[101],t[101];
const int inf=0x3f3f3f3f;
int main()
{
scanf("%lld%lld",&n,&s);
for(int i=1; i<=n; i++)
scanf("%lld %lld",&v[i],&t[i]);
for(int i=0; i<=s; i++)//initialization
for(int j=0; j<=5200; j++)
dp[0][i][j]=-inf*(j!=2600);
//This place cannot move 2600, because 2600 is the solution, and the solution is 0 at the beginning
for(int i=1; i<=n; i++)
for(int j=0; j<=s; j++)
for(int k=0; k<=5200; k++)
{
dp[i][j][k]=dp[i-1][j][k];
if(k>=t[i])dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k-t[i]]+v[i]);
//Load T
if(k+t[i]<=5200)dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k+t[i]]+v[i]);
//Load S
if(j&&k>=2*t[i])dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-1][k-2*t[i]]+v[i]);
//Load S after doubling
if(j&&k+2*t[i]<=5200)dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-1][k+2*t[i]]+v[i]);
//Load T after doubling
}
printf("%lld\n",dp[n][s][2600]);
return 0;
}
Title J
The latter two questions haven't been fully understood yet. We'll fill them in after we understand them.