3-5/3-9 Quick Sort Correlation

Posted by freeak08 on Sat, 15 Jan 2022 07:58:53 +0100

Catalog

1. Quick Sort

Version 1.1:

2 Derived problems of merge sort and quick sort

2.1 Inverse Order Pair Problem

2.2 Take the nth largest element in the array

1. Quick Sort

Version 1.1:

Intermediate process:

Finally:

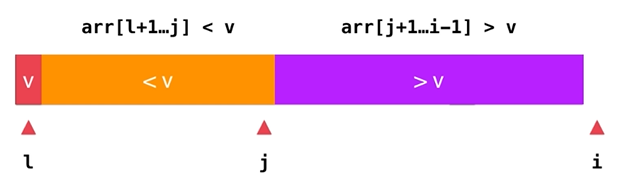
In this case, you only need to exchange the elements at the l and j positions:

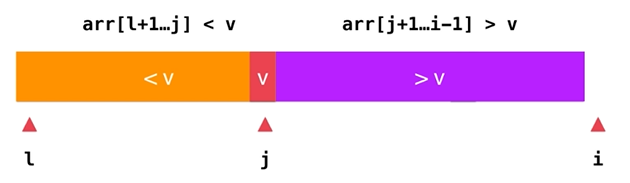
//partition operation on arr[left...right} section
//Returns P such that arr[left...p-1]<arr[p], arr[p+1...r]>arr[p]
int __partition(int arr[],int left,int right)
{
    int v=arr[left];
    int j=left; //Initial reference pictures of i and j
    for(int i=left+1;i<=right;i++)
    {
        if(arr[i]<v)
        {
            swap(arr[i],arr[j+1]);
            j++;
        }
    }
    swap(arr[left],arr[j]);
    return j;
}

//Quickly sort the arr[left...right} section
void __quickSort(int arr[],int left,int right)
{
    if(left>=right)
        return;
    int p=__partition(arr,left,right);
    __quickSort(arr,left,p-1);
    __quickSort(arr,p+1,right);
    return;
}

void quickSort(int arr[],int n)
{
    __quickSort(arr,0,n-1);
    return;
}

Version 1.2 2 2:

As with merge sort improvements, insert sort can be used to improve performance when data size is small

Simply modify u quickSort function, the others are the same:

//Quickly sort the arr[left...right} section
void __quickSort(int arr[],int left,int right)
{
    if(right-left<=15)
    {
        insertionSort(arr,left,right);
        return;
    }
        
    int p=__partition(arr,left,right);
    __quickSort(arr,left,p-1);
    __quickSort(arr,p+1,right);
    return;
}

Version 1.3 3 3:

Quick sorting results in a recursive tree that is poorly balanced than merge sorting and does not guarantee that the tree height is logn

The worst case for quick sorting is when the array is nearly ordered and degenerates to O(n^2)

This happens because we now fixed the leftmost element as the calibration element.

Improvement: Randomly select one element as the calibration element:

//partition operation on arr[left...right} section
//Returns P such that arr[left...p-1]<arr[p], arr[p+1...r]>arr[p]
int __partition(int arr[],int left,int right)
{
    swap(arr[left],arr[rand()%(right-left+1)+left]); //Change 2: Find an element randomly and swap arr[left]
    int v=arr[left];
    int j=left; //Initial reference pictures of i and j
    for(int i=left+1;i<=right;i++)
    {
        if(arr[i]<v)
        {
            swap(arr[i],arr[j+1]);
            j++;
        }
    }
    swap(arr[left],arr[j]);
    return j;
}

//Quickly sort the arr[left...right} section
void __quickSort(int arr[],int left,int right)
{
    if(right-left<=15)
    {
        insertionSort2(arr,left,right);
        return;
    }

    int p=__partition(arr,left,right);
    __quickSort(arr,left,p-1);
    __quickSort(arr,p+1,right);
    return;
}

void quickSort(int arr[],int n)
{
    srand(time(NULL));//Change 1: Set random seeds
    __quickSort(arr,0,n-1);
    return;
}

Version 1.4 4 4:

For arrays with a large number of repeating elements, previous versions are less efficient

As you can see from the figure below, for arrays with a large number of repeating elements, the partition operation is likely to divide the array into extremely unbalanced parts

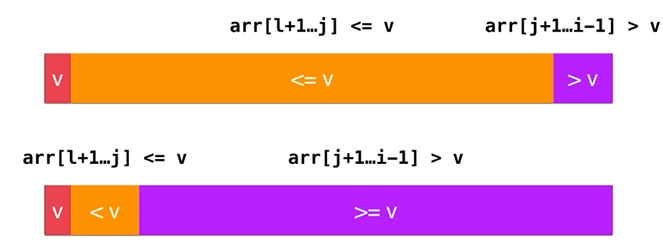
New ideas:

Previously, you put everything less than v and greater than v on one side of the array, now you put them on the left and right sides respectively:

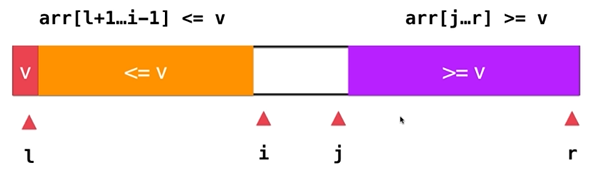
i Scan back and forth until an element greater than or equal to v is encountered

j scans backwards and forwards until it encounters an element less than or equal to v

The difference between this method and the previous one is that the elements equal to v are spread to the left and right sides, which is more balanced.

//partition operation on arr[left...right} section
//Returns P such that arr[left...p-1]<=arr[p], arr[p+1...r]>=arr[p]
int __partition(int arr[],int left,int right)
{
    swap(arr[left],arr[rand()%(right-left+1)+left]); //Randomly find an element and exchange arr[left]
    int v=arr[left];
    int i=left+1; //Initial reference pictures of i and j
    int j=right;
    /*while(i<j)
    {
        while(i<j&& arr[i]<v)
            i++;
        while(i<j&& arr[j]>v)
            j--;
        if(i<j)
        {
            swap(arr[i],arr[j]);
            i++;
            j--;
        }
    }*/
    while(true)
    {
        while(i<=right && arr[i]<v)
            i++;
        while(j>=left && arr[j]>v)
            j--;
        if(i>j)
            break;
        swap(arr[i],arr[j]);
        i++;
        j--;
    }

    swap(arr[left],arr[j]);
    return j;
}

//Quickly sort the arr[left...right} section
void __quickSort(int arr[],int left,int right)
{
    if(right-left<=15)
    {
        insertionSort2(arr,left,right);
        return;
    }

    int p=__partition(arr,left,right);
    __quickSort(arr,left,p-1);
    __quickSort(arr,p+1,right);
    return;
}

void quickSort(int arr[],int n)
{
    srand(time(NULL));//Set up random seeds
    __quickSort(arr,0,n-1);
    return;
}

Version 1.5 5 5:

Another way to improve on large numbers of elements--three-way quick sorting

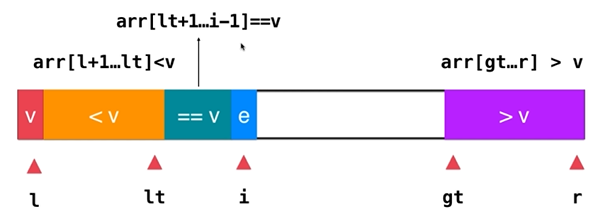
By dividing the whole array into three parts, the part equal to v is not considered in the recursion process, only the other two parts need to be recursively the same.

//Quickly sort the arr[left...right} section
void __quickSort(int arr[],int left,int right)
{
    if(right-left<=15)
    {
        insertionSort(arr,left,right);
        return;
    }

    //partition
    swap(arr[left],arr[rand()%(right-left+1)+left]);
    int v=arr[left];
    int lt=left;
    int gt=right+1;
    int i=left+1;
    while(i<gt)
    {
        if(arr[i]==v)
            i++;
        else if(arr[i]>v)
        {
            swap(arr[i],arr[gt-1]);
            gt--;
        }
        else
        {
            swap(arr[i],arr[lt+1]);
            lt++;
            i++;
        }
    }
    swap(arr[i],arr[lt]);
    lt--;
    __quickSort(arr,left,lt);
    __quickSort(arr,gt,right);
    return;
}

void quickSort(int arr[],int n)
{
    srand(time(NULL));//Set up random seeds
    __quickSort(arr,0,n-1);
    return;
}