Ideas for Block Search

Before explaining the blocking algorithm, let's introduce the concept of blocking lookup

• Concepts: Block lookup, also known as index order lookup, requires an index table based on the lookup table in addition to the algorithm implementation. Given a lookup table, its corresponding index table is shown in the figure:
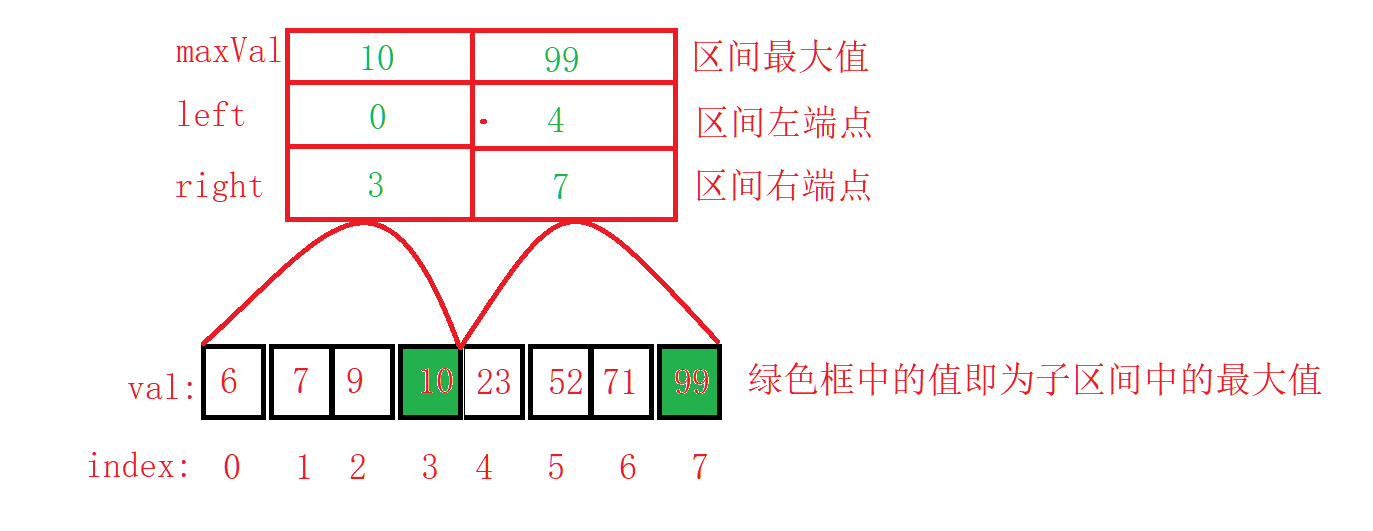
• Interpretation: Looking at the index tables corresponding to the two sub-intervals [0, 3] and [4, 7] in the figure above, we can see that for an index table, the maximum value of the interval is 1, the left end of the interval is 2, and the right end of the interval is 3. This is also the block in the block search we are talking about, so the index table summarizes the information of a block.
• When we talk about the algorithm ideas below, the index tables will be understood as blocks without special instructions.

Explain the relevant concepts, and let's start with the idea of block search.

• The basic idea of block search:

1. First, the lookup table is divided into several subblocks. Elements within a block can be disordered or ordered, but the blocks are ordered as a whole (the elements in the array interval [0, 3] above are all smaller than those in [4, 7]). Generally speaking, all recorded keywords in the second block are larger than the largest keyword in the first block, all recorded keywords in the third block are larger than the largest keyword in the second block, and so on. This kind of ordering is block ordering.
2. For the value val we are looking for, there are two steps: 1. For ordered subblocks, we use half-fold search (or sequential search), we first determine which subblock the value should be in (or may not be found), and 2. For found subblocks, we use only direct sequential search. (Because in practice it is basically out of order, and for basic order it is also out of order, and only sequential lookup can be used).

Now let's introduce a related case.

1. This is an experimental question about data structure course in the author's school.
2. For this problem, it is obviously a block search algorithm design problem. We first create a table with a data volume of 1000, then create it in four parts. For example, in the first part, we randomly store every number from 1 to 250 in the range [0, 249]. This means that each number in this part is unique, and the other three parts are created in the same way. Finally, the data range of the overall table is [1, 1000]. And each number is unique.
3. Next, we fold each block in half to find the block where Val is located. Search sequentially for found blocks to find val.

Half-fold lookups for each block are different from half-fold lookups for ordinary integers and need to be explored further.

• Q: For blocks [2, 4, 6, 7] (each number represents the largest keyword in each block), how do we determine which block we belong to by counting 0, 3, 9, respectively? Look at it separately.

• For 0:

• For 3:

• For 9:

• Only by analyzing the above three situations, can we grasp the full grasp when facing the block search!

C Code - Running in VS2019

#define _CRT_SECURE_NO_WARNINGS 1
#define pages 1000

/*
* Create an index table of the number of pages in a Book [1,1000]
*/
#include <stdio.h>
#include <assert.h>

// Index table
typedef struct
{
	int maxValue; // Maximum keyword in selected block
	int left;     // Left endpoint of interval where block is located
	int right;    // Right endpoint of interval where block is located
}IndexTable;


// Just to test tile lookups. Normal index tables do not need to be written by themselves
IndexTable* InitIndexTable()
{
	//  Open up an array space of index tables of size 4
	IndexTable* res = (IndexTable*)malloc(sizeof(IndexTable) * 4);

	// Indexing information, default index tables are strictly ascending by keyword
	for (int i = 0; i < 4; i++) {
		res[i].maxValue = 250 * (i + 1);
		res[i].left  = i * 250;
		res[i].right = 250 * (i + 1) - 1;
	}

	return res;
}

int BlockingSearch(int* nums, IndexTable* table, int tableSize, int targetVal)
{
	// 1. Find the block first
	int begin = 0, end = tableSize - 1;
	int mid = (begin + end) / 2;
	
	int targetBlock = 0;
	// For dichotomy block finding, there are two boundary cases, requiring special judgment
	// 1. begie is out of bounds; 2. end is out of bounds.
	while (begin <= end)
	{
		if (table[mid].maxValue < targetVal)
		{
			begin = mid + 1;
		}
		else if (table[mid].maxValue > targetVal)
		{
			end = mid - 1;
		}
		else
		{
			targetBlock = mid;
			break;
		}

		mid = (begin + end) / 2;
	}
	// 
	if (begin > end)
	{
		// In general, we must look for the target value in the begin block
		targetBlock = begin;
		// begin is out of bounds
		// The targetVal exceeds all the key values in the index table, which must not be found.
		if (begin > tableSize - 1) return -1; 
		// end out of bounds
		// The tagetgetVal is smaller than all the key values, but it is not guaranteed that it will not be found because the key values are the maximum values in each subinterval.
		if (end < 0) targetBlock = begin;
	}

	// 2. Since the elements within the block are out of order, we search within the block sequentially
	for (int i = table[targetBlock].left; i < table[targetBlock].right; i++)
	{
		if (nums[i] == targetVal) return i;
	}

	return -1;
}

int main()
{
	int index[pages];
	int val = 0;
	FILE* pF = NULL;
	assert(pF = fopen("pagesRandom.txt", "r"));

	for (int i = 0; i < pages; i++) assert(fscanf(pF, "%d", &index[i]));
	IndexTable* table = InitIndexTable();
	printf("Enter the value of the keyword you need to find:");
	assert(scanf("%d", &val));
	int res = BlockingSearch(index, table, 4, val);


	// This statement cannot be written like this. In C, 0 is false, not 0 is true, so it is also true for negative numbers.
	if (res >= 0)
	{
		printf("%d The index in the original data is:%d\n", val, res);
	}
	else
	{
		printf("No target value in original array%d\n", val);
	}
	return 0;
}

Test data address: pagesRandom.txt