The last part introduced How to Construct FP Tree Each path of FP tree satisfies minimum support. What we need to do is to find more relationships on one path.

Extraction of conditional pattern bases

Start with a single frequent element item in the FP tree header pointer table. For each element item, the corresponding conditional pattern base is obtained, and the conditional pattern base of a single element item is also the keyword of the element item. The conditional schema base is a set of paths ending with the element item being searched. Each path is actually a perfix path. In short, a prefix path is everything between the element item being searched and the root node.

The following figure is a prefix path with {s:2} or {r:1} as element items:

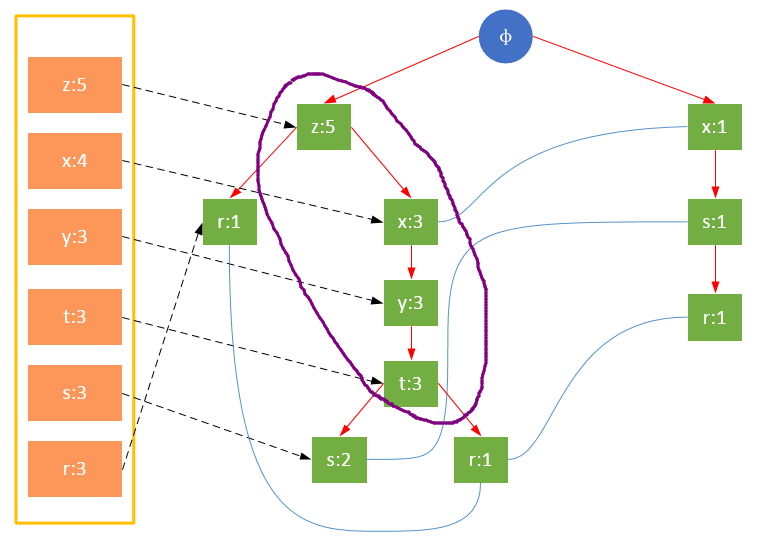
There are two conditional pattern bases of {s}, i.e. the set of prefix paths: {z,x,y,t}, {x}; and {r} three conditional pattern bases: {z}, {z,x,y,t}, {x,s}.

The process of finding conditional pattern bases is actually a process of tracing back from each leaf node of FP tree to the root node. We can start with the headTable of the header pointer list and quickly access all the root nodes through the connection of the pointer. The following table is the base of all conditional patterns of the FP tree in the above figure:

Create conditional FP tree

In order to find more frequent itemsets, a conditional FP tree is created for each frequent item. You can use the conditional schema base just discovered as input data and build these trees with the same tree building code. Then, frequent items are found recursively, conditional pattern bases are found, and other conditional trees are found.

Taking frequent item r as an example, the conditional FP tree about R is constructed. The three prefix paths of R are {z},{z,x,y,t},{x,s} respectively. If the minimum support minSupport=2, then y,t,s are filtered out, leaving {z},{z,x},{x}. y,s,t are not conditional FP trees, although they are part of the conditional schema base. That is to say, they are not frequent for R. As shown in the figure below, the global support of y t r and S R is 1, so y,t,s are not frequent for the conditional tree of R.

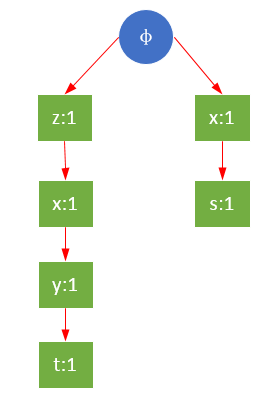
The filtered r condition tree is as follows:

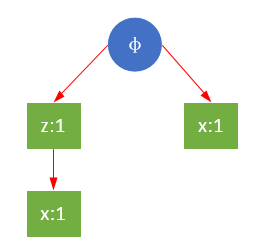
Repeat the steps above. The conditional pattern bases of r are {z,x},{x}, and there is no path that can satisfy the minimum support, so there is only one conditional tree of r. It should be noted that although {z,x} and {x} have two x, in {z,x}, Z is the parent node of X. When constructing the condition FP tree, the parent node can not be removed directly, but can only be removed step by step from the child node. If {x,z}, a conditional FP tree with only {x} nodes can be constructed in this round. This is exactly what I said in the previous article. The order of items will affect the final result.

The code is as follows:

 1 def ascendTree(leafNode, prefixPath):
 2     if leafNode.parent != None:
 3         prefixPath.append(leafNode.name)
 4         ascendTree(leafNode.parent, prefixPath)
 5 
 6 def findPrefixPath(basePat, headTable):
 7     condPats = {}
 8     treeNode = headTable[basePat][1]
 9     while treeNode != None:
10         prefixPath = []
11         ascendTree(treeNode, prefixPath)
12         if len(prefixPath) > 1:
13             condPats[frozenset(prefixPath[1:])] = treeNode.count
14         treeNode = treeNode.nodeLink
15     return condPats
16 
17 def mineTree(inTree, headerTable, minSup=1, preFix=set([]), freqItemList=[]):
18     # order by minSup asc, value asc
19     bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: (p[1][0],p[0]))]
20     for basePat in bigL:
21         newFreqSet = preFix.copy()
22         newFreqSet.add(basePat)
23         freqItemList.append(newFreqSet)
24         # Frequent itemsets found through conditional schema bases
25         condPattBases = findPrefixPath(basePat, headerTable)
26         myCondTree, myHead = createTree(condPattBases, minSup)
27         if myHead != None:
28             print('condPattBases: ', basePat, condPattBases)
29             myCondTree.disp()
30             print('*' * 30)
31 
32             mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
33 
34 simpDat = loadSimpDat()
35 dictDat = createInitSet(simpDat)
36 myFPTree,myheader = createTree(dictDat, 3)
37 myFPTree.disp()
38 condPats = findPrefixPath('z', myheader)
39 print('z', condPats)
40 condPats = findPrefixPath('x', myheader)
41 print('x', condPats)
42 condPats = findPrefixPath('y', myheader)
43 print('y', condPats)
44 condPats = findPrefixPath('t', myheader)
45 print('t', condPats)
46 condPats = findPrefixPath('s', myheader)
47 print('s', condPats)
48 condPats = findPrefixPath('r', myheader)
49 print('r', condPats)
50 
51 mineTree(myFPTree, myheader, 2)

Console information:

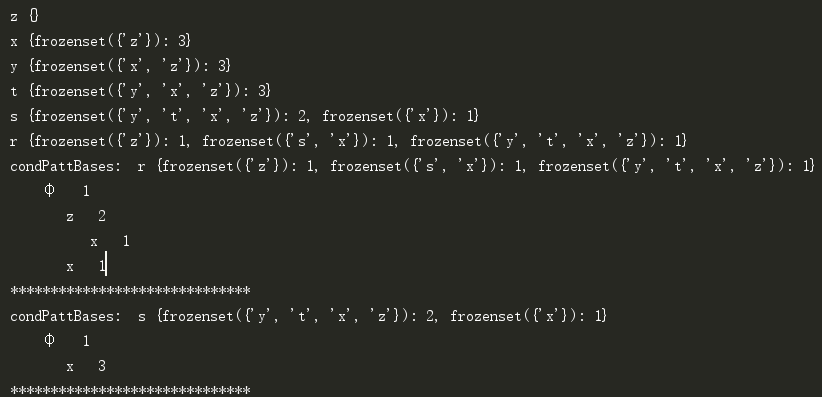
This example can find two frequent itemsets {z,x} and {x}.

After acquiring frequent itemsets, association rules can be found according to confidence. This step is relatively simple, and can refer to the relevant content of the previous chapter, not to be redundant.

Reference: Machine Learning Practice

Author: I am eight.

Origin: http://www.cnblogs.com/bigmonkey

This paper focuses on learning, research and sharing. If you need to reproduce, please contact me, indicating the author and origin, non-commercial use!