This paper is from Introduction to Algorithms of Netease Open Course, Lecture 3, Dividing and Curing. Let me have a new understanding of the use of the division method Fibonacci sequence, also known as the golden section sequence, F0=0, F1=1, F n = F (n-1) +F (n-2) (n > = 2, n < N*)

Next, I'll use Java (yes, Java again, but I don't think it's a problem. Algorithms, ideas) to implement these three methods separately. Later, half of the video shows that there are many repetitive sub-problems when using naive recursive method to solve the problem. This is in line with the basic idea of dynamic programming. We can use bottom-up order to save the results of the sub-problems. The algorithm time to do this is: theta(n)

Naive recursion: Solving problems from the top down leads to a large number of repetitive solutions.

2. Dynamic programming: To be exact, it should be a bottom-up "dynamic programming" solution.

3. Mathematical Induction (Linear Algebraic Matrix Continuous Multiplication Formula)

Let Fn denote the nth Fibonacci number, then there is a theorem:

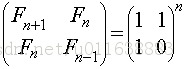
Prove that when n=1,F0=0,F1=1,F2=2, that is:

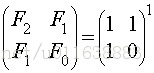
Suppose the theorem holds, then n-1 is brought into the available expression:

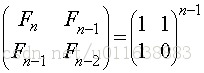
That is:

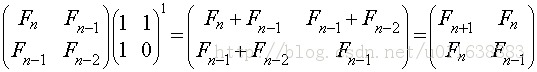
Because of the equation

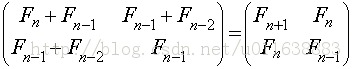
Constancy holds, so hypothesis holds.

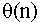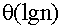In this way, the Fibonacci sequence is transformed into the n-multiplier problem, so why not the algorithm time of the n-multiplier problem?ButWhat about it? In this paper, divide and conquer method can be used to solve the n-multiplier problem. The n-multiplier can be divided into two equal parts (n/2 and n/2 for even d, n-1/2 and (n-1)/2 for odd number). There are:

In this way, n numbers multiplied by one another only need to be partitioned.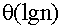Second time is enough.

The code is as follows:

package com.wly.algorithmproblem;

/**
 * Three methods are used to solve the Fibolacci sequence problem: simple recursive method, bottom-up dynamic programming method and linear algebraic matrix multiplication formula method.
 * @author wly
 * @date 2013-11-28 
 *
 */
public class FibonacciSequence {
	
	private static int TESTCASE = 43;
	
	private static int[][] matrixUnit = {{1,1},{1,0}};
	
	public static void main(String[] args) {
		
		System.out.println("Test scale:" + TESTCASE);
		
		//Testing of Simple Recursive Solution to Fibonacci Sequence Problem
		long startT = System.currentTimeMillis();
		System.out.println("Naive recursion:" + simpleRecurrence(TESTCASE));
		System.out.println("Naive recursive usage time:" + (System.currentTimeMillis()-startT));
		
		//Bottom-up (Dynamic Programming) Test for Solving Fibonacci Sequence Problem
		startT = System.currentTimeMillis();
		System.out.println("Bottom-up(dynamic programming):" + downToTopReslove(TESTCASE));
		System.out.println("Bottom-up(dynamic programming)Use time:" + (System.currentTimeMillis()-startT));
	
		//Testing of Solving Fibonacci Sequence Problem by Linear Algebraic Matrix
		int[][] mResult = {{1,1},{1,0}};
		startT = System.currentTimeMillis();
		int n = 1;
		while(n<TESTCASE) {
			mResult = matrixMutiple(mResult, matrixUnit);
			n ++;
		}
		System.out.println("Linear Algebraic Matrix Formula:" + mResult[0][1]);
		System.out.println("Time Use of Linear Algebraic Matrix Formula:" + (System.currentTimeMillis()-startT));

		//n-multiplication test of dividing and conquering method for m
		System.out.println("Dividing and Conquering Method for 23 Continuous Multiplication of 2:" + pow(2, 23));
	
		//Test of Two Matrix Multiplication Method
		/*
		int[][] matrix1 = {{2,3,4},{1,2,3}};
		int[][] matrix2 = {{2,4},{3,5},{4,6}};
		int[][] result = new int[matrix1.length][matrix2[0].length];
		int[][] resultS = matrixMutiple(matrix1,matrix2,result);
		System.out.println();
		*/
		
	}
	
	
	/**
	 * Naive recursion
	 * @param n 
	 * @return The nth Fibonacci Number
	 */
	public static int simpleRecurrence(int n) {
		if(n == 0) {
			return 0;
		} 
		if(n == 1 || n == 2) {
			return 1;
		}
		
		return simpleRecurrence(n-1) + simpleRecurrence(n-2);
	}
	
	/**
	 * Solution Method Including "Dynamic Programming" Thought from Bottom to Top
	 * @param n
	 * @return The nth Fibonacci Number
	 */
	public static int downToTopReslove(int n) {
		if(n == 0) {
			return 0;
		} else if(n == 1 || n == 2) {
			return 1;
		} else {
			int[] fibonacciArray = new int[n+1]; //Fibonacci Array [i] denotes the first Fibonacci number
			fibonacciArray[0] = 0;
			fibonacciArray[1] = 1;
			fibonacciArray[2] = 1;
			for(int i=3;i<=n;i++) { //Note that since Fibonacci Array [0] represents element 0, here is i<=n, not i<n
				fibonacciArray[i] = fibonacciArray[i-1] + fibonacciArray[i-2];
			}
			
			return fibonacciArray[fibonacciArray.length-1];
		}
	}
	
	
	/**
	 * Divide and conquer method to solve factor's n-th power
	 * @param factor base
	 * @param n Dimensional Number
	 * @return
	 */
	public static long pow(long factor,int n) {
		if(n == 0) {
			return 1;
		} else if(n == 1){
			return factor;
		} else {
			if(n % 2 == 1) { //Multiplication is odd
				return pow(factor,(n-1)/2) * pow(factor, (n-1)/2) * factor;
			} else { //Multiplier is even
				return pow(factor, n/2) * pow(factor, n/2);
			}
		}
	}
	
	/**
	 * Multiplication of two matrices
	 * @param matrix1
	 * @param matrix2
	 * @return
	 */	
	public static int[][] matrixMutiple(int[][] matrix1,int[][] matrix2) {
		int[][] result = new int[matrix1.length][matrix2[0].length];
		for(int i=0;i<matrix1.length;i++) {
			for(int j=0;j<matrix2[i].length;j++) {
				int temp = 0;
				for(int k=0;k<matrix1[0].length;k++) {
					temp = matrix1[i][k] * matrix2[k][j] + temp;
				}
				result[i][j] = temp;
			}
		}
		return result;
	}
}

Test scale: 43
 Naive recursion: 433494437
 Naive Recursive Time: 1669
 Bottom-up (dynamic programming): 433494437
 Bottom-up (dynamic programming) time: 0
 Linear algebraic matrix formula: 433494437
 Linear algebraic matrix formulas: 1
 Divide and Conquer 2 by 23 multipliers: 8388608

One thing to note here is that the code already contains the n-th power of m.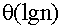Code. It was originally intended to be combined with the solution of the third linear algebraic matrix continuation multiplication, but later it was found that in that case, the code was very messy, so it was simply realized by using while to multiply n times. Generally speaking, we have realized three different methods to solve Fibolacci sequence, hoping that we can give you some reference.

O la~~~

Reproduced from:

Thank you!