Standard Origin: http://www.cnblogs.com/wy123/p/6970721.html
Disclaimer:
This article is only for entertainment, from the point of view of winning or losing the lottery, to analyze how to invest to achieve the "most secure" income, ^ O^
This article does not have any guidance or responsibility for any actual investment portfolio.
Introduction of Winning, Balancing and Losing as well as betting on portfolio scheme
Reading standard requires a little basic knowledge of football. ^O^
The characteristics of winning, losing and losing are based on the results of a single match. Winning, drawing and losing for the home team are different from the aggregation of the results of combined N games.
This paper focuses on the "single-game portfolio", which means that there are three premises.
First, a single game.
Second, the amount of investment is fixed.
Thirdly, there are more than one alternative.
Under these three conditions, how to maximize profits according to the odds?
For example,
Referring to the following picture, Sweden's 2017-06-09-06-1002:45 World Cup qualifying match against France is held in the European Championship.
The home team's winning odds are 5.25, the draw odds are 3.50, and the home team's negative odds are 1.53.
For the current game, for example, ready to put out 50 yuan to bet on the game.
To meet the first condition above, a single match, while meeting the second condition, fixed investment amount
For example, we are optimistic about the French team. For the sake of safety, we can bet that the match will be a draw or the home team (Sweden) will lose. That is to say, we can bet that the French team will not lose (draw or win).
The betting scheme mentioned here satisfies condition three and is larger than an investment scheme.

Assuming that the odds remain unchanged, the two alternatives, when preparing to invest 50 yuan, how to calculate the maximum collection according to the odds
For example, scheme 1 is a tie with 30 hosts holding 20, and scheme 2 is a tie with 30 hosts holding 20.
If the final result is that the home team wins, normally speaking, this possibility is the least. The two bets are totally wrong and the profit is 0.
If the final result is a tie between the two teams, the possibility is general. The income of scheme 1 is 3.50*20=70, and that of scheme 2 is 3.50*30=105.
If the final result is negative for the home team, the probability is higher. The income of scheme 1 is 1.53*20 = 30.60, and that of scheme 2 is 1.53*30 = 45.90.
It can be seen that in the case of more than one betting scheme, different combination schemes have different benefits in the face of different outcomes.
High returns are bound to face high risks. For example, to bet directly on Sweden's victory over France, the probability of gains is high, but the probability of betting is low.
If we need to be safe here, we must lose potential gains. The safest thing is to make money in custody no matter how much we earn.
So in the selected situation, how to distribute the amount of the bet, in order to achieve the relative "most secure", that is to say, to ensure as much as possible to make money, not how much.
T-SQL realizes the most secure portfolio
Simply implement it with T-SQL
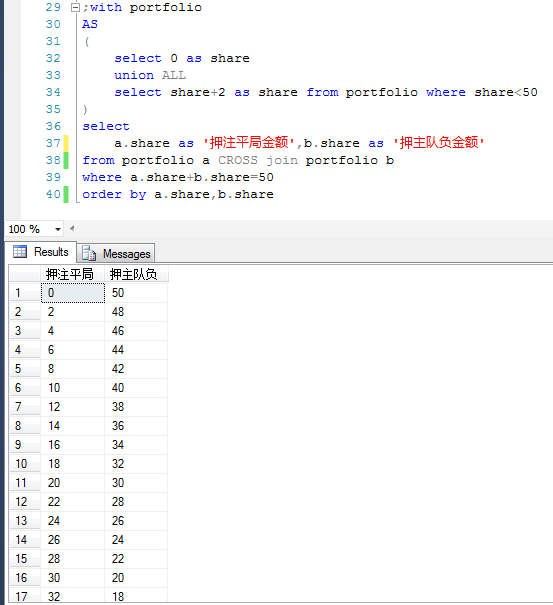
As shown below, with the help of the recursive function of ct, the amount invested in this game is 50 yuan, and all possible portfolios are calculated.
The following is the possibility of all portfolios under current conditions if the home team is equal or the home team is negative.
On the basis of the above results, the following are the returns of different portfolios on the basis of corresponding odds.
For the selected results, the two are mutually exclusive. Either way, the risks and potential benefits of different combinations are different.
For example, in the first combination, the draw is 0 yuan, and the home team is 50 yuan. The worst result is that the two teams are even. At this time, the profit is 0 and the loss is 50 yuan.
For example, in the second combination, the tie is 2 yuan, and the home team is 48 yuan. The worst result is the tie between the two teams. At this time, the profit is 7 and the loss is 43 yuan.
With the increase of the amount of the tie, the amount of the negative bet on the home team decreases. The worst result will be 50 yuan of the tie, 0 yuan of the negative bet on the home team, 0 yuan of the return and 50 yuan of the loss.
But there will be a more ideal situation, the draw is 16 yuan, the home team negative 34 yuan, at this time whether the draw or the home team negative, are "profitable".
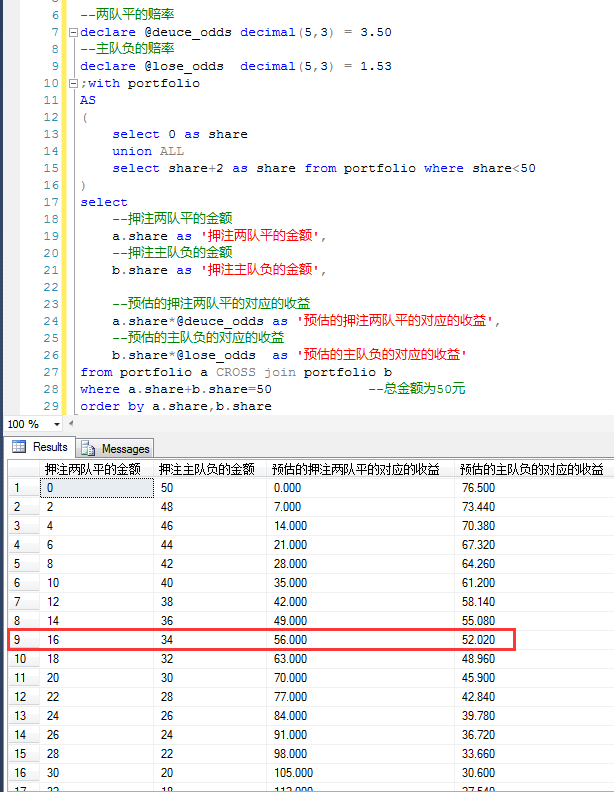
The returns and risks in all the above portfolios are different.
"The safest" here is to ensure profits rather than maximize profits.
How to rationally allocate the amount of bets between different schemes? That is to say, the first choice is to ensure profitability and maximize the possibilities. The amount of profitability exceeds the total investment.
The following can be queried to get the most secure revenue portfolio.
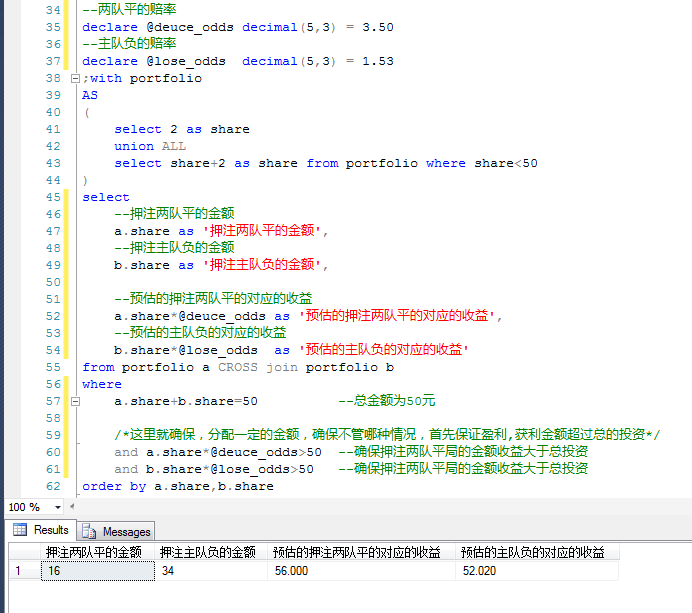
Then look at another World Cup qualifying match between the Faroe Islands and Switzerland. The odds of winning and losing are 16.5, 6.6 and 1.09, respectively.

According to the above calculation method, we still choose the two schemes of the home team's equalization or the home team's negative, and find that there is no so-called "the safest scheme" mentioned above.
This means that there is no plan to ensure that profits are made in the event of a draw or a negative home team.
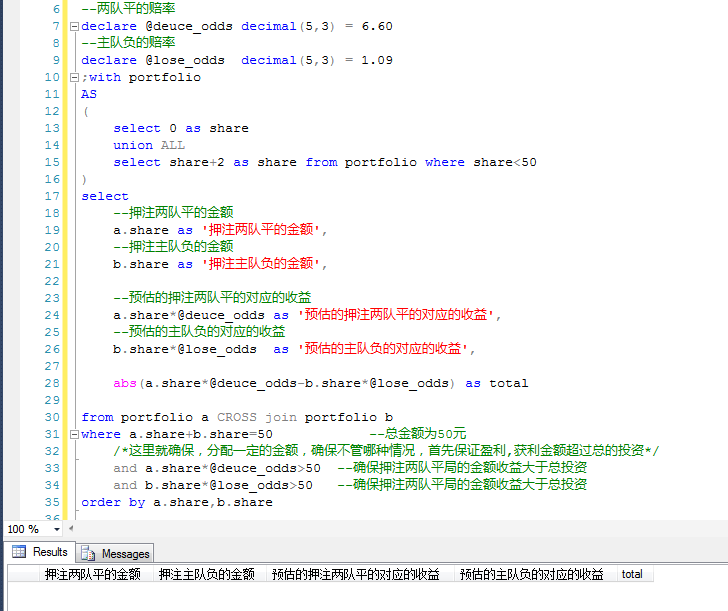
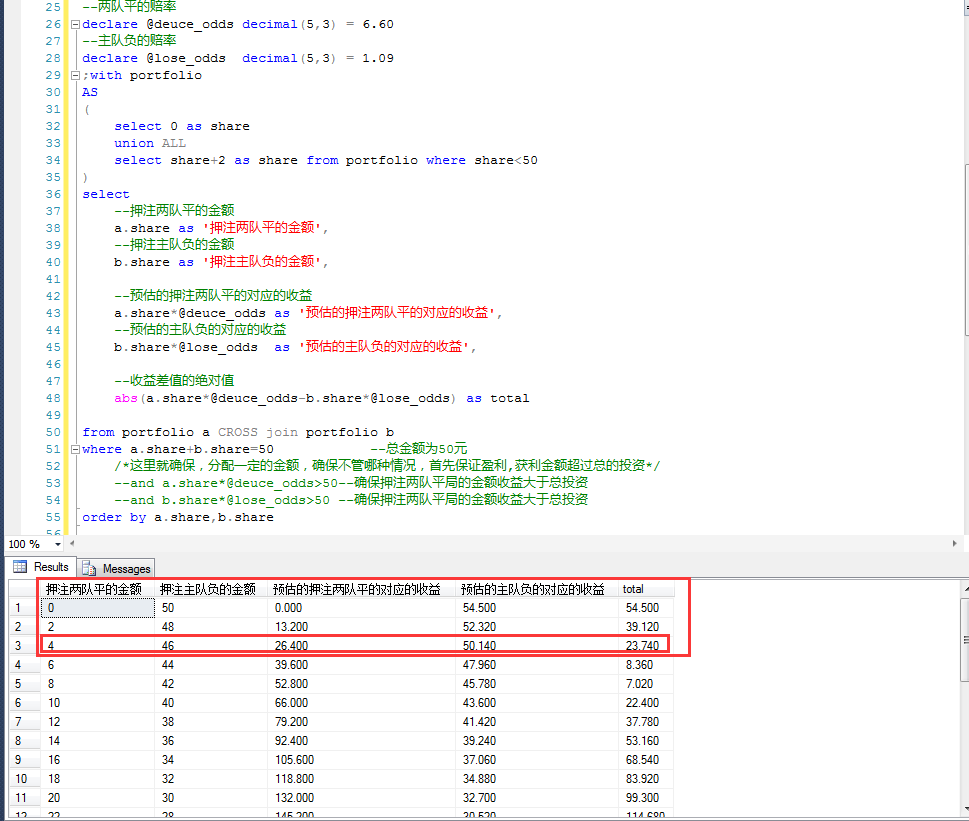
What if you still want to buy the game? If it is in the premise of striving for stability, the above algorithm can still calculate a relatively stable scheme.
It's a very big possibility for the home team to lose this game.
First of all, we can choose the negative profit scheme of the home team, and then we can bet as little as possible on the situation of the draw between the two teams to ensure that we can recover some losses in case of a relatively small chiller.
That is to say, in the two schemes, the first one is to ensure the negative profit of the home team. On this premise, the difference between the draw and the negative profit of the home team is the smallest.
In fact, it is not difficult to understand that the above considerations are as follows.
1. First of all, make sure that the home team loses profits, because the home team loses is a probability event.
2. The income gap between the draw and the negative return of the home team is the smallest, so as to ensure that losses are minimized when the draw is too cold.
This is a result of throwing out emotional factors and calculating rationally, although the returns do not look good.
Finally, the standard test script is attached.
--The odds are even between the two teams. declare @deuce_odds decimal(5,3) = 6.60 --The home team's negative odds declare @lose_odds decimal(5,3) = 1.09 ;with portfolio AS ( select 0 as share union ALL select share+2 as share from portfolio where share<50 ) select --Bet on the equal amount of the two teams a.share as 'Bet on the equal amount of the two teams', --Bet on the negative amount of the home team b.share as 'Bet on the negative amount of the home team', --Predicted bets on the corresponding earnings of the two teams a.share*@deuce_odds as 'Predicted bets on the corresponding earnings of the two teams', --The predicted negative return of the home team b.share*@lose_odds as 'The predicted negative return of the home team' --Absolute value of earnings margin --abs(a.share*@deuce_odds-b.share*@lose_odds) as total from portfolio a CROSS join portfolio b where a.share+b.share=50 --The total amount is 50 yuan. /*This ensures that a certain amount of money is allocated to ensure that, in any case, profit is guaranteed first, and the amount of profit exceeds the total investment.*/ --and a.share*@deuce_odds>50 --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment --and b.share*@lose_odds>50 --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment order by a.share,b.share
Again, this article is for entertainment only, without any guidance or suggestions for any excitement.
Encapsulated as a stored procedure, aspect calls
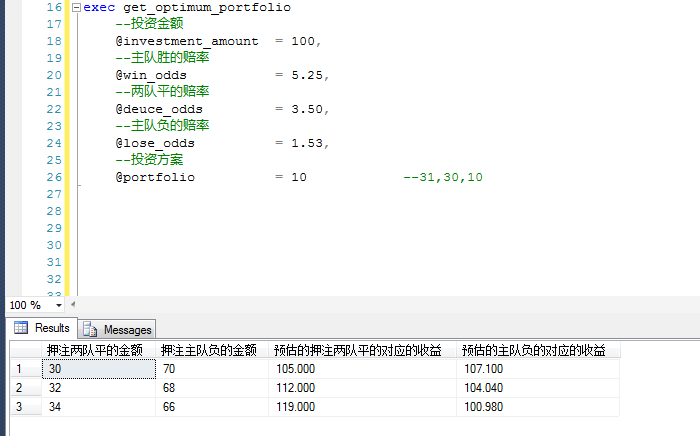
create proc get_optimum_portfolio ( --Amount of investment @investment_amount int, --The odds of home team winning @win_odds decimal(10,3), --The odds are even between the two teams. @deuce_odds decimal(10,3), --The home team's negative odds @lose_odds decimal(10,3), --Portfolio options @portfolio INT --31,30,10,31 They represent the home team unbeaten, 30 represent the winner or loser, and 10 represent the visiting team unbeaten. ) as begin if(@investment_amount<=0) begin ;throw 50000,'@investment_amount must be greater than 0',1 end if(@investment_amount%2<>0) begin ;throw 50000,'@investment_amount can not be odd number',1 end if(@portfolio<>30 and @portfolio<>31 and @portfolio<>10) begin ;throw 50000,'@portfolio must be one of 31,30,10',1 end /* declare @investment_amount int --The odds of home team winning declare @win_odds decimal(5,3) = 6.60 --The odds are even between the two teams. declare @deuce_odds decimal(5,3) = 6.60 --The home team's negative odds declare @lose_odds decimal(5,3) = 1.09 */ ;with portfolio AS ( select 0 as share union ALL select share+2 as share from portfolio where share < @investment_amount ) select * into #portfolio from portfolio; if exists ( select 1 from #portfolio a CROSS join #portfolio b where a.share+b.share = @investment_amount --Total amount /*This ensures that a certain amount of money is allocated to ensure that, in any case, profit is guaranteed first, and the amount of profit exceeds the total investment.*/ and a.share*@deuce_odds>@investment_amount --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment and b.share*@lose_odds>@investment_amount --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment --order by a.share,b.share ) begin select --Bet on the equal amount of the two teams a.share as N'Bet on the equal amount of the two teams', --Bet on the negative amount of the home team b.share as N'Bet on the negative amount of the home team', --Predicted bets on the corresponding earnings of the two teams a.share*@deuce_odds as N'Predicted bets on the corresponding earnings of the two teams', --The predicted negative return of the home team b.share*@lose_odds as N'The predicted negative return of the home team' --Absolute value of earnings margin --abs(a.share*@deuce_odds-b.share*@lose_odds) as total from #portfolio a CROSS join #portfolio b where a.share+b.share = @investment_amount --Total amount /*This ensures that a certain amount of money is allocated to ensure that, in any case, profit is guaranteed first, and the amount of profit exceeds the total investment.*/ and a.share*@deuce_odds>@investment_amount --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment and b.share*@lose_odds>@investment_amount --Ensuring that the amount of money earned by betting on a tie between the two teams is greater than the total investment order by a.share,b.share end else begin select top 1 * from ( select --Bet on the equal amount of the two teams a.share as N'Bet on the equal amount of the two teams', --Bet on the negative amount of the home team b.share as N'Bet on the negative amount of the home team', --Predicted bets on the corresponding earnings of the two teams a.share*@deuce_odds as N'Predicted bets on the corresponding earnings of the two teams', --The predicted negative return of the home team b.share*@lose_odds as N'The predicted negative return of the home team', --Absolute value of earnings margin abs(a.share*@deuce_odds-b.share*@lose_odds) as difference_val from #portfolio a CROSS join #portfolio b where a.share+b.share = @investment_amount --Total amount /*This ensures that a certain amount of money is allocated to ensure that, in any case, profit is guaranteed first, and the amount of profit exceeds the total investment.*/ and (a.share*@deuce_odds >= @investment_amount or b.share*@lose_odds >= @investment_amount) )t order by difference_val asc end end
Examples of calls