The pictures are all from Mucho. com, just for learning records.
1. Binary Search Tree
It can also be called a binary search tree. It can not only find data, but also insert and delete data efficiently.
Features: The key value of each node is larger than that of the left sub-node and smaller than that of the right sub-node. Note that it is not necessarily a complete binary tree.
So the key of the node is unique, and we index the corresponding value of the key through it. Note that all the keys in the graph are marked.


Therefore, binary search trees are not suitable to be represented by arrays, and they are usually represented by node nodes.
Advantages over the data structure of arrays:


Another advantage is that its keys can be defined by itself, such as String as a key to implement a lookup table, while arrays can only be indexed


2. Realization.
Implement each node first:
The elements of a node are key, value, left and right sub-nodes.
public class Node {//Node's keyprivate int mKey;//Value value corresponding to Nodeprivate int mValue;//The left and right sub-nodes are null in the initial state.private Node mLeftChild;private Node mRightChild;public Node(int key,int value){mKey = key;mValue = value;mLeftChild = null;mRightChild = null;}public int getValue(){return mValue;}public Node getLeftChild(){return mLeftChild;}public Node getRightChild(){return mRightChild;}public void setValue(int newValue) {mValue = newValue;}public void setLeftChild(Node left) {mLeftChild = left;}public void setRightChild(Node right) {mRightChild = right;}public int getKey(){return mKey;}}
Basic Implementation of Binary Search Tree
package com.zy.serch;/*** Binary Search Tree* @author Administrator**/public class BinarySearchTree {//Root node.private Node mRoot;//There should also be a value to record quantities, and each insert should add 1 to the data.private int mCount;public int getSize(){return mCount;}//Sentence blankpublic boolean isEmpty(){return mCount == 0;}}
Implementation of inserting data
/*** For external invocation* @param key key of data to be stored externally* @param value Value of data to be stored externally*/public void insert(int key,int value){//Further invoke the internal insert to place the current key and value in the tree with mRoot as the root node.mRoot = insert(mRoot, key, value);}/*** Insert a node.* The core idea is to find the insertion position from the root node to satisfy the characteristics of the binary search tree, which is larger than the left sub-node and smaller than the right sub-node.* Steps:* 1,Starting with the root node, compare the current node, and if the current node is null, it is obvious that it should be inserted into the node.* 2,If the above node is not null, then compared with the current node, if it is smaller than the node, it will be placed in the left subtree, and if it is larger than the node, it will be placed in the right subtree.* 3,Then, the recursive operations of the left subtree or the right subtree are performed in steps 1 and 2 above respectively.** Recursion is used at this point, so recursion is a problem, its sub-problems need to be the same model.* A minor problem here is that a node is then manipulated, so the parameter should have a node in order to loop.* Insert the node (key, value) into the binary search tree with node as its root. Here, the int type is used, and the external user is* You don't need to understand the concept of node. They just need to know the key and value passed in.* Temporary design makes it easy to understand the keys and value s that are passed into the user's own, and then it's also convenient to use them according to keys.** @param node Because to use the idea of recursion, it's time to insert nodes.* @param key Externally imported key* @param value External incoming value* @return Returns the heel of the binary tree after the new insertion of the binary tree node.*/private Node insert(Node node,int key,int value){//If the node to be inserted is null, then prove that we have found the location, just put it here.if(node == null){//Quantity plus 1mCount++;//But then when it's the first place to insert it, it's returned.return new Node(key, value);}//If the current node already has nodes (do not consider duplication? )//Here we compare the values of value.if(key < node.getKey()){//At this point, the left node should be processed recursively. The inserted node is finally put into the left child node.//Ultimately related to the left subtree.Node left = insert(node.getLeftChild(), key, value);node.setLeftChild(left);}else if(key > node.getKey()){// // At this point, the left node should be processed recursively. The inserted node should finally be placed in the right child node.Node right = insert(node.getRightChild(), key, value);node.setRightChild(right);}else{//Update the value directly when equal tonode.setValue(value);}return node;//Return to the root node}
Implementation of query data:
/*** Find the corresponding value according to the key value.* @param key The key to look up* @return Returns the value corresponding to the key, and returns null if the lookup fails.**/public int serch(int key){//Call internal functions recursively.return serch(mRoot,key);}/**** @param node The first entry is the root node, which is indexed from the root node. After searching, the next entry is the next one to be searched.* @param key The key value to look for.* @return Returns the value corresponding to the key found.*/private int serch(Node node,int key){//Certificate not found, directly return to the processing when not foundif(node == null){return (Integer) null;//What's better if you don't find something to return to?}//The following is a comparison of the keys to be searched and the keys to the current Node in turn:// If equal: it proves that the current value has been returned directly// If the key to be searched is less than the key of the current node: then go to the left child of the current node to search recursively.// If the key to be searched is larger than the key of the current node: then the right child of the current node is searched recursively.if(node.getKey() == key){return node.getValue();//Look at it so that the key is unique and the key on the right is larger than the key on the left? You didn't guess wrong, haha, at first you got it wrong, Toury.//The value of all faces is key, not value.}else if (key < node.getKey()){//Processing on the left, continue processing the number of left subnodes, and return directly after finding. (Not very well understood here)//Here the function can be returned, and go directly to the next function recursively to find, the return value of this function is one.//The return value of the next function, so recursive.return serch(node.getLeftChild(), key);}else{return serch(node.getRightChild(), key);}}
Does the query contain any data?
/*** Determine whether the key pair corresponding to the current key exists in the binary search tree* @param key The key to look for* @return Existence returns true, and none returns false.*/public boolean contain(int key){return contain(mRoot,key);}//Realizing ideas is the same as searching, after all, to see if it's really the process of searching.private boolean contain(Node node,int key){if(node==null){return false;}if(node.getKey() == key){return true;//Look at it so that the key is unique and the key on the right is larger than the key on the left?}else if (key < node.getKey()){//Processing on the left, continue processing the number of left subnodes, and return directly after finding. (Not very well understood here)return contain(node.getLeftChild(), key);}else{return contain(node.getRightChild(), key);}}
The Mu lesson net test is designed with string as key and number of occurrences as value. This way of searching binary trees loops over blocks in while rather than sequentially
Quite a lot.
Traversal of binary search tree.
Traversal refers to making one visit to each node in the tree in turn along a search route. There are three kinds of traversing binary trees:
Preorder Traversal: First visit the current node, then recursively access the left and right subtrees.
Inorder Traversal: First, access the left subtree recursively, then access itself, then access the right subtree recursively
Postorder Traversal: Visit the left and right subtrees recursively, and then the current node.
How do you understand the first kind of recursive access above? For example, if the left sub-node of any node has not been visited, continue to visit its left sub-node until the left sub-node has finished.
After the complete traversal, the first node to be visited will be traversed in intermediate order, and then up in sequence.
These three kinds of order are the order of the current node (that is, the middle one).
Find the picture above Baidu:


Preorder traversal: A B C D E F G
Mid-order traversal: C B D A E F G
Post-order traversal: C D B G F E A
You can see that in general, the order of front, middle and back is relative to the current node, and will recursively go deep into the last layer of the node. Then from the bottom floor
Each node is executed in a specified order.
The last sequence traversal: traversal from top to bottom, left to right.
Sequence traversal: A B E C D F G
Preorder traversal:
/*** Preorder traversal* Traveling through this block is easy to implement with recursive thinking, so the smallest size is for a node, and the function should have a parameter Node.*/public void perTravelsal(){//Traverse from the root nodeperTravelsal(mRoot);}private void perTravelsal(Node node){//You don't have to go down until the node is nullif(node != null){//For each node, the current node is traversed first.//Let's simply print the key value for traversal.System.out.print(node.getKey()+" ");//Then we recursively execute the left subtree, paying attention not to judge whether there is, because we will judge when we go in.perTravelsal(node.getLeftChild());//Recursive Execution of Right SubtreeperTravelsal(node.getRightChild());}}
Intermediate traversal
/*** An application of mid-order traversal is that it is orderly after traversal.*/public void inorTravelsal(){//Call the internal recursive implementation.inorTravelsal(mRoot);}//Specific recursive implementationprivate void inorTravelsal(Node node){if(node!=null){//Traversing the left node firstinorTravelsal(node.getLeftChild());//Then the current nodeSystem.out.print(node.getKey()+" ");inorTravelsal(node.getRightChild());}}
Postorder traversal
/*** Postorder traversal*/public void postTarvelsal(){//The reason is the same as the first two.postTarvelsal(mRoot);}private void postTarvelsal(Node node){if(node!=null){//Traversing the left node firstpostTarvelsal(node.getLeftChild());//Then the right child nodepostTarvelsal(node.getRightChild());//Finally, the current nodeSystem.out.print(node.getKey()+" ");}}
level traversal
/*** level traversal* What we mentioned earlier is that depth-first traversal is achieved by recursion. As long as the downward nodes have the required conditions, they will continue to execute west-first and downward.* Sequence traversal is a breadth-first traversal method. First traverse the root node layer, then traverse the second layer, so from top to bottom, from left to right.* The idea here is to take advantage of the first-in-first-out (FIFO) feature of the queue.* When the queue is not empty, start the operation. If the queue is not empty, then the root node must exist. First, the root node should be replaced by the root node.* Enter the team, and then start a circular judgment: judge the condition queue as kong, first traverse the current node, then leave the queue, (at this time the queue is empty)* Then see if there are left and right sub-nodes in this node, if there is a queue (so it is not empty, and down a layer), left and right sub-nodes.* When the node has finished processing, continue to do the same operation in a loop.*/public void levelTravelsal(){//Require queue coordination, first instantiate a queueQueue<Node> queue = new BlockingQueue<Node>() {//......};//If no element is returned directly.if(isEmpty()){return;}//There are elements to prove that the minimum root node is not null. First-in. Cyclic exit condition?//No elements in the queue? Layer by layer?//Get the Root Node into the Team Firstqueue.add(mRoot);while(!queue.isEmpty()){//As long as it is not empty, the current node is processed first and the front element in the queue is removed.Node node = queue.poll();//Do traversal operation when leaving the queueSystem.out.print(node.getKey()+" ");//When the left node is not null, join the left node in the queueif(node.getLeftChild()!=null){queue.add(node.getLeftChild());}//Add the right node to the queue when the left node is not nullif(node.getRightChild()!=null){queue.add(node.getRightChild());}//So if the current node has left and right nodes, the queue will not be null.//When we continue to cycle to the front, we first take out the front node (we put it in left-right order).//So the next cycle is to take the current node out of the queue, traverse the operation, and then the right node out of the queue traverse the operation.//Then continue to see if there are left and right nodes, so that the sequence traversal is achieved.}}
Get the maximum and minimum
/*** Find the node with the smallest value, and return the key of the found node, after all, the user passes in the key and value.* Can't find it is returning null.* @return The key corresponding to the node with the smallest value.*/public int getMinmum(){if(isEmpty())return (Integer) null;//Recursive calls to internal implementations.Node min = getMinmum(mRoot);return min.getKey();}private Node getMinmum(Node node){/*//Don't worry that node is null, because if it's root node, it won't get in at all.//If it's not the root node, we return directly when the left is null.Node left = node.getLeftChild();if(left != null){//Processing recursively when not null.getMinmum(left);}else{//The left child of the current node is null, which proves that the minimum value has been found.return node;}return node;*///Below is God's concise code! Although the meaning is the sameNode left = node.getLeftChild();if(left == null){return node;}//Otherwise, call it recursively to execute its left child nodereturn getMinmum(left);}//Get the maximum node, just like the minimum node, according to the characteristics//Find the lowest child node of the right subtree./*** Get the node with the largest value* @return The node with the largest value corresponds to the key.*/public int getMammum(){if(isEmpty())return (Integer) null;Node max = getMammum(mRoot);return max.getKey();}private Node getMammum(Node node){Node right = node.getRightChild();if(right == null){return node;}return getMammum(right);}
Delete the maximum and minimum values of the binary search tree.
Delete the smallest node
//Delete the minimum value of the binary search tree. Learn to delete the maximum and minimum values first.//Because when the maximum and minimum values are deleted, the current node, that is, the largest/smallest node, will not have two sub-nodes.//When the minimum value is deleted, either the current node has no child nodes or the current node has only one right child node. (It's not the smallest when you have left child nodes)//When the maximum value is deleted, either the current node has no children, or the current node has only one left child. (It's not the smallest when there are right subnodes)/*** Delete the smallest node from the binary tree**/public void removeMin(){/*//First, you should find the smallest node.Node min = getMinmum(mRoot);if(min == null)return;//If the current node has a right child, place the node on the index of the parent of the smallest nodeif(min.getRightChild()!=null){//How to get the parent of the smallest node? At this point, we do not set the attributes of the parent node, so we need to find a little bit.//This plan is not good.}*///So you can only search again and delete it when you find it.//Need to find out, or continue to use recursion better understanding, the next call to the internal deletion functionif(isEmpty()){return;}removeMin(mRoot);}/**** @param node Initially, it passes in the root node, a mirror operation, and a value into the node on the left subtree.* Set the right subtree node in until the smallest node is deleted and return it to the parent node.* (Actually, it's not good enough to understand.** @return Returns the root of the new binary search tree after deleting the node.In fact, it is the root of the node of the initial incoming binary tree.*/private Node removeMin(Node node){Node left = node.getLeftChild();if(left == null){//It is proved that the smallest node has been found.//Start deleting, feel that java is nothing to do, release the node? ,//Should first get the right sub-node, whether or not, no is to get a null.Node right = node.getRightChild();node = null;//Release the memory of the current nodemCount--;//Number of nodes--//Note that the return value here does not affect the return value of the final function. The return value of this block is only when it reaches the smallest node.//Return the right subtree of the current smallest node and cooperate (note that in the last function call, that is, the parent of the smallest node)//setLeftChild implements setting the node of the right subtree to the node of the left subtree of the parent.return right;}//The following recursion, when not reaching the smallest node, will always be stuck here and pay attention to not reaching the return node.//When the card is here, the first value is passed in to the current node's left node, and the left node is always set up.//Until you enter the smallest node, return to the right child of the smallest node, and then set it layer by layer. Finally, the root node is returned.Node temp = removeMin(left);node.setLeftChild(temp);return node;}
Delete the largest node
/*** Removing the largest node is the same as removing the smallest node.*/public void removeMax(){if(isEmpty()){return;}removeMax(mRoot);}/**** @param node The current node that requires removeMax() function operation.* @return It returns the root node of the binary tree where the removed node is located, which is actually the root of the node of the original incoming binary tree.*/private Node removeMax(Node node){//Get the right child nodeNode right = node.getRightChild();//When null equals null, it turns out that the largest one has been found.if(right == null){//Remove its left child node, whether or not it hasNode left = node.getLeftChild();node = null;//Delete the current nodemCount--;return left;//Return this to set the right child for the parent node}Node temp = removeMax(right);node.setRightChild(temp);return node;}
Delete any node:
/*** Delete any node: A method proposed by Hibbard called Hubbard Deletion*The difference between deleting any node and deleting the smallest and largest node is that when deleting any node, it is possible to have both left and right sub-nodes.*First of all, we can't simply put the left or right child nodes in the position of the currently deleted node, because this is the case.*It is easy to cause dissatisfaction with the characteristics of binary search tree. We should find the current precursor or put it in the current position.*An element smaller than it; a successor: an element smaller than it hits. For example, in one way, we find all the nodes in its right child node.*The smallest node in the tree, and then put the smallest node into the deleted node, which still satisfies the characteristics of the binary search tree, the left sub-node.*They are smaller than it, and the right child nodes are larger than it. A similar approach is to find the largest node of all nodes in the left subtree.*Delete steps when finding the node to be deleted: (when there are only left or right sub-nodes, use the previous, determine that there are both left and right nodes)* 1,Find the minimum value of the right child node and delete it.* 2,Then put the deleted node in the location where it was found.* That is to assign the right and left child nodes of the found node to the deleted node respectively.* 3,Finally, the node should also assign the correct location to the parent of the deleted node.*All of these are implemented by looking up. You can't call the interface directly to find the node you want to delete, so you can't get it here.*Its parent node cannot be associated.* @param key The key of the node to be deleted is because we designed the key to be int.**/public void remove(int key){//Internal or Call Recursive Ideas for ImplementationmRoot = remove(mRoot,key);}private Node remove(Node node,int key){//The first node to join, when internal remove() is called, still passes in root//If an empty node proves to have found the lowest level, it is not found.if(node == null){return null;//Just go back to empty.}//Note that the search is from the root node side.//If it is found that it is larger than the right child node, then continue to search for the right child node.if(key > node.getKey()){//It should recursively go to the right. The whole understanding below is not in place.Node right = node.getRightChild();//Continue to pass in the right node in the same way as the previous maximum/smallest understanding.//When you don't get to the bottom, it's at the parent node level: always pass in the child node on the right, and then//The value returned is set to the current right child node (because this function returns the current node and we pass in the right child node)//This is where the loop recurs until:// 1. If we don't find the node to delete, we will eventually go to node = null, which is the last layer.// The return is null assigned to the right of the parent node, and then returned recursively to the upper layer until the first layer of the incoming node.// There's nothing wrong with setting their right child nodes.// 2. When we find the node we want to delete, let's assume that the node is called D. Then we won't go to the last level.// Break, and go to the equivalent time judgment we designed below, in which we will return to the forerunner or successor we found, and then// This node is mounted under the right child of its parent node. This completes the linking of the entire binary tree.Node temp = remove(right, key);node.setRightChild(temp);return node;//Return to the current node, which is the first node to be passed in.}else if(key < node.getKey()){//Reason is the same as aboveNode left= node.getLeftChild();Node temp = remove(left, key);node.setLeftChild(left);return node;} else {//This is the time to find the node to delete.//There will be three more situations://The first is that the node found does not have a left child, which is similar to deleting the minimum value.//At this point, a node represents the node to be deleted.if(node.getLeftChild() == null){//Get the right nodes directly, return them, and let them assign values one layer at a time, regardless of whether null or not.Node right = node.getRightChild();mCount--;node = null;return right;}//The second is that the node found does not have a right child, which is similar to deleting the maximum value.if(node.getRightChild() == null){//Ibid.Node left = node.getLeftChild();mCount--;node = null;return left;}//Third, when there are sub-nodes left and right, this is our Hubbard deletion.//Here we use the successor of finding and deleting nodes, which is the minimum value of the right subtree.//So you should first find the smallest node of the right subtree, multiplex getMinmum(node) and pass it to the right child of the current node.Node min = getMinmum(node.getRightChild());//Then removeMin is reused to delete the node. At this time, instead of passing in the root node, the right child node of the current node is passed in.//In this way, the value of the smallest node in all subtrees rooted on the right child of the current node is deleted and the incoming right child node is returned.//Internally, the index of that node in the binary tree will be null, but we got the new index in front of us, which also points to that place.Node rightRoot = removeMin(node.getRightChild());//Just assign the root of this right subsection to the right subnode of the min found.min.setRightChild(rightRoot);//Then you need to connect the left child of the deleted node to the left child of the found node.//Node is the node to be deleted.min.setLeftChild(node.getLeftChild());node = null;//mCount--;//At this point, I feel like I will subtract one more. In the previous remove, I subtract the smallest one, and then I subtract the current node.//But there is no mCount++ when connecting the smallest node found to the binary search tree.//mCount++; // Cable is not -- No.return min;//Returns the judgment of the two left and right subnodes used for the first judgment key.}}
The time complexity of deleting any node in the binary search tree is O(logn), and the time complexity of deleting a node in the sequence table is O(n).
3. Expanding Knowledge
On the sequentiality of binary search trees.
Forerunners and successors:
On the predecessor of a number: predecessor [pri:d ses(r)] predecessor/predecessor. On the successor of a number: successor [s k ses(r)]heir
For the precursor and successor of a number, the existence of this number is required, and the precursor and successor functions need to be considered when implementing:
1) Whether the current node is the minimum, there is no precursor at the minimum; similarly, whether it is the maximum, the maximum has no succession.
2) Whether there are two left and right sub-nodes, if so, the precursor will go to the left sub-node to find the maximum, and then go to the right sub-node to find the minimum.
3) embarrassment analysis can not come out. When the left and right child nodes are incomplete or none, it feels troublesome. Your consideration is that the current node is the child of the parent node, which is harmful.
It's messy to consider the situation of parents with fewer children. I don't know yet, but it's also arranged according to the order of key s in the end. Is it better to find it?
floor and ceil
The floor and ceil functions do not need the key s to be looked up, and if they exist, the value of the two functions is the return itself.
floor: The value corresponding to the key that is not larger than the incoming key is
ceil: no less than the value of the key passed in is

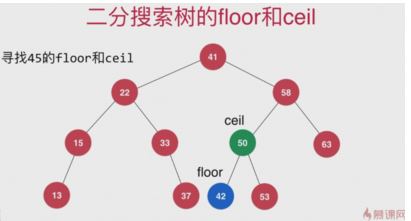
Implementation of floor
/*** According to the key of the incoming node, the key of the corresponding node after floor operation is obtained.** @param key The key of the node to floor* @return The key of the result node of the corresponding floor, if there is no return null.*/public int floor(int key){//If the mCount in the binary tree is 0, or less than the lowest value, then there is no precursorif(mCount==0||key < getMinmum()){return (Integer) null;}//Call floor of the internal implementation.Node node = floor(mRoot, key);return node.getKey();}// In the binary search tree rooted by node, the node where the floor value of key is located is searched.private Node floor(Node node, int key){//Return null directly when the current node is null.if( node == null )return null;// If the key value of the node is equal to the key value to be looked for, the node itself is the floor node of the key.if( node.getKey() == key )return node;// If the key value of the current node is larger than the key value to be searched for, then the precursor must be in the left node.if( node.getKey() > key )//Go to the left node for recursive lookupreturn floor( node.getLeftChild() , key );// At this point, the key of the current node is less than the key to be looked up.// 1) At this point, the node is the floor corresponding to the key node.// 2) The node is not the floor corresponding to the key node, because there is a smaller value in the right node of the current node than the key of the node.// That is, there are other nodes larger than node - > key but smaller than key.// We need to try to find the right subtree of node. Generally speaking, the understanding is not deep, but the whole feeling should be recursive.// Consider only the current node situation, do not try to go one layer after another to consider the internal, only consider the current time, is to go to the right node and recursive search.// If found, return it, if not. Prove that the current node (smaller than key) is correct. Then return to the current nodeNode tempNode = floor( node.getRightChild() , key );//If we find a proof that there is a smaller direct returnif( tempNode != null )return tempNode;//When we get here, group Hengming satisfies node. getKey () < key, and there is no smaller one in the right subtree of this node!return node;}
The implementation of ceil is equivalent to floor
public int ceil(int key){//If the mCount in the binary tree is 0, or less than the lowest value, then there is no precursorif(mCount==0||key > getMammum()){return (Integer) null;}//Call floor of the internal implementation.Node node = ceil(mRoot, key);return node.getKey();}private Node ceil(Node node ,int key){//Return null directly when the current node is null.if(node == null){return null;}if(key == node.getKey()){return node;}//When the key is larger than the key of the current node, it means that we should go to the right subtree to find the minimum value larger than the key.//You can't be less than key.if(key > node.getKey()){return ceil(node.getRightChild(), key);}//See if the left node has a key larger than the key but smaller than the current node's key.Node tempNode = ceil( node.getLeftChild() , key );if( tempNode != null )return tempNode;//If there is a return to this//Otherwise, return to the current node.return node;}
Ranking of Binary Search Books
Want to know where a key in the binary search tree ranks in the book?


One way to achieve this is to add a field for each tree node, which marks how many sub-nodes the current node has, and then it can be calculated by simple logic and calculation.
What's the ranking?
Note that adding a domain record like this is the most difficult way to maintain the corresponding domain when insert and remove, so don't forget.
Binary Search Tree Supporting Duplicate Elements
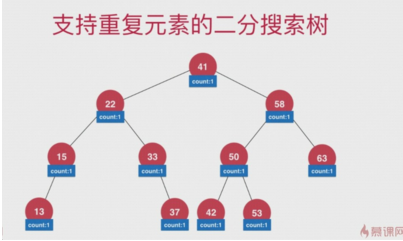
The first implementation is to place the larger node in the right sub-node and the smaller or equal node in the left sub-node. But this wastes space when there are a lot of repetitive elements.
The second implementation: also add a domain to Node, which is used to mark the number of current nodes.
Limitations of binary search trees.


When the insertion order of data is close to order, the binary search tree may degenerate into a linked list, and the time complexity changes from logn to n.
But we can't mess up the elements at once, because it's possible that you can't get all the elements you type in a little bit of data. At this point, the improved binary tree:
The implementation of balanced binary tree includes:
1) Red and Black Trees
2),2-3 tree
3),AVL tree
4),Splay tree
5) Treap balanced binary tree and heap combination.
Balanced Binary Tree has the following properties: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and the left and right subtrees are both balanced binary trees.
These are some concepts, and there are many things to learn. When we wait for the second time, we should study them in depth and in detail. There are also trie trees, word search trees.
There are other kinds of trees:
KD tree (k-dimensional tree for short) is a data structure that divides k-dimensional data space. It is mainly applied to the search of key data in multi-dimensional space (e.g.
Circumference search and nearest neighbor search. K-D tree is a special case of binary space partitioning tree.
Interval Tree: Interval Tree is an operation that supports the dynamic set of intervals as elements based on the red-black tree, in which the key value of each node is the interval.
Left endpoint.
Huffman tree: Given n n n weights as n leaf nodes, a binary tree is constructed. If the length of weighted path reaches the minimum, such a binary tree is called the optimal binary tree.
Tree, also known as Huffman Tree. Huffman tree is the shortest tree with weighted path length, and the node with larger weights is closer to the root.
The solution of various games is the search of binary tree.