Strongly Connected Components
brief introduction
Before reading the following, be sure to understand Graph Theory Basis Part.
The definition of strong connectivity is: strong connectivity of digraph G means that any two nodes in G are connected.
Strongly Connected Components (SCC) is defined as a large strongly connected subgraph.
What I want to introduce here is how to find strongly connected components.
Tarjan algorithm
Robert E. Tarjan (1948 ~) American.
Tarjan invented many algorithms. There are many Tarjan algorithms, such as Tarjan algorithm for all kinds of interconnection components and Tarjan algorithm for LCA (Lowest Common Ancestor, recent common ancestor). And search, Splay, Toptree were invented by Tarjan.
Here we introduce the Tarjan algorithm for finding strongly connected components in directed graphs.
In addition, Tarjan's name j is not pronounced and translated into Tayan in Chinese.
DFS spanning tree
Before introducing the algorithm, we first understand the DFS spanning tree. Let's take the following digraph as an example:
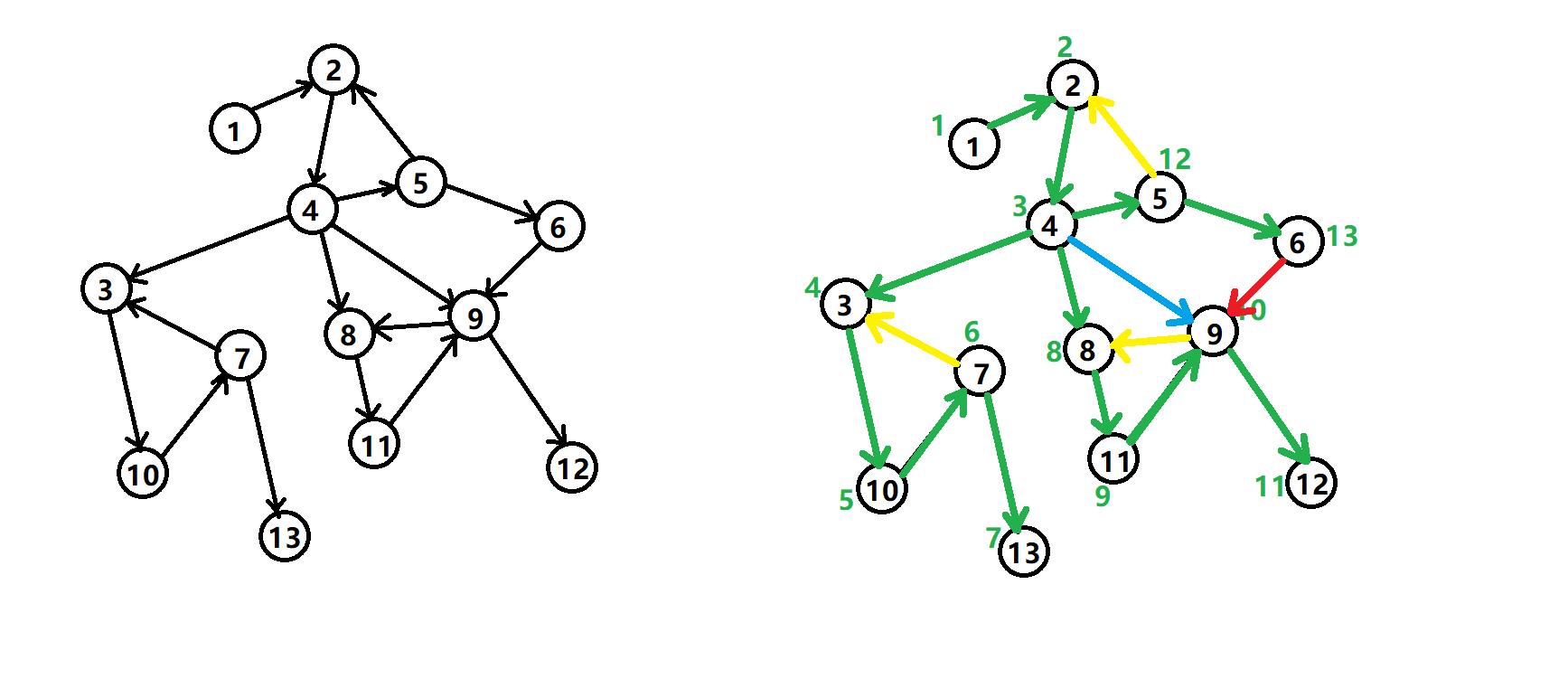
DFS spanning trees of digraphs have four kinds of edges (not all of them appear):
- Tree edge: Green edge, which forms a tree edge every time a search finds a node that has not yet been visited.
- Back edge: The yellow edge, also known as the back edge, points to the edge of the ancestral node.
- cross edge: Red edge, which is mainly a node that has been visited while searching, but this node is not formed by the ancestors of the current node.
- forward edge: Blue edge, which is formed when a search encounters a node in a subtree.
We consider the relationship between DFS spanning tree and strongly connected components.
If the node u is the first node that a strongly connected component encounters in the search tree, then the rest of the nodes of the strongly connected component must be in the subtree rooted by u in the search tree. U is called the root of this strongly connected component.
Conversion: Assuming that there is a node V in the strongly connected component but not in the subtree rooted by u, there must be an edge away from the subtree in the path from u to v. However, such edges can only be crossed or anti-ancestor edges. However, the nodes that both sides require to point to have been visited, which contradicts the fact that u is the first node to visit. Evidence.
Tarjan algorithm for strongly connected components
In the Tarjan algorithm, the following variables are maintained for each node u:
- DFN[u]: The order in which nodes are searched during depth-first search traversal.
- LOW[u]: Let the subtree rooted in u be Subtree(u). LOW[u] is defined as the minimum value of the following nodes: the node in Subtree(u); the node from Subtree(u) through an edge not on the search tree.
The DFN of the node in the subtree of a node is larger than that of the node.
DFN on a path starting from the root increases strictly while LOW does not decrease strictly.
All the nodes in the graph are searched according to the order of depth-first search algorithm. In the search process, three cases are considered for the node and its adjacent node (v is not the parent of u):
- V is not accessed: continue to search for V in depth. In the retrospective process, LOW[v] is used to update LOW[u]. Because there is a direct path from u to v, so V can trace back to the node already in the stack, u must also be able to trace back.
- V has been visited and has already been visited on the stack. According to the definition of LOW value (the earliest node that can be traced back to already on the stack), the LOW[u] is updated with DFN[v].
- v has been visited and is no longer in the stack: it means that v has been searched and its connected component has been processed, so it is not necessary to operate on it.
Write the above algorithm into pseudo-code:
1 TARJAN_SEARCH(int u) 2 vis[u]=true 3 low[u]=dfn[u]=++dfncnt 4 push u to the stack 5 for each (u,v) then do 6 if v hasn't been search then 7 TARJAN_SEARCH(v) // search 8 low[u]=min(low[u],low[v])// To flash back 9 else if v has been in the stack then 10 low[u]=min(low[u],dfn[v])
For a connected component graph, it is easy to think that there is only one DFN[u]=LOW[u] in the connected component graph. The node must be the first one to be visited in the depth traversal process, because its DFN and LOW values are the smallest and will not be affected by other nodes in the connected component.
Therefore, in the process of backtracking, the condition of DFN[u]=LOW[u] is determined to be valid. If it is valid, a SCC is formed from the node behind u in the stack.
Realization
1 int dfn[N], low[N], dfncnt, s[N], tp; 2 int scc[N], sc; // node i where scc Number of ____________ 3 int sz[N]; // Strongly Connected i Size 4 void tarjan(int u) { 5 low[u] = dfn[u] = ++dfncnt, s[++tp] = u; 6 for (int i = h[u]; i; i = e[i].nex) { 7 const int &v = e[i].t; 8 if (!dfn[v]) 9 tarjan(v), low[u] = min(low[u], low[v]); 10 else if (!scc[v]) 11 low[u] = min(low[u], dfn[v]); 12 } 13 if (dfn[u] == low[u]) { 14 ++sc; 15 while (s[tp] != u) scc[s[tp]] = sc, sz[sc]++, --tp; 16 scc[s[tp]] = sc, sz[sc]++, --tp; 17 } 18 }
Time complexity O(n+m).
Kosaraju algorithm
Kosaraju algorithm relies on two simple DFS implementations.
For the first DFS, any vertex is selected as the starting point, and all visited vertices are traversed, and the number of vertices is given before backtracking, that is, post-traversal.
The second DFS starts with the maximum labeled vertex as the starting point for the backward graph. The set of vertices traversed in this way is a strongly connected component. For all unvisited nodes, select the largest label and repeat the above process.
After two DFS, the strongly connected components are found. The time complexity of Kosaraju algorithm is O(n+m).
Realization
1 // g It's the original picture. g2 It's an inverse graph. 2 3 void dfs1(int u) { 4 vis[u] = true; 5 for (int v : g[u]) 6 if (!vis[v]) dfs1(v); 7 s.push_back(v); 8 } 9 10 void dfs2(int u) { 11 color[u] = sccCnt; 12 for (int v : g2[u]) 13 if (!color[v]) dfs2(v); 14 } 15 16 void kosaraju() { 17 sccCnt = 0; 18 for (int i = 1; i <= n; ++i) 19 if (!vis[i]) dfs1(i); 20 for (int i = n; i >= 1; --i) 21 if (!color[s[i]]) { 22 ++sccCnt; 23 dfs2(s[i]) 24 } 25 }
Garbow algorithm
application
We can reduce every strongly connected component of a graph to a point.
Then the graph becomes a DAG (why?).
DAG is good, you can do a lot of things if you can sort the topology.
For a simple example, finding a path can go through repeated nodes, requiring the largest number of different nodes to go through.
Recommended topics
USACO Fall/HAOI 2006 Popular Cattle
Next, let's discuss what Tarjan algorithm can do:
Since we know that the Tarjan algorithm is equivalent to finding a directed ring in a digraph, the most direct ability of our Tarjan algorithm is the hot reduction point! Reduction point is based on a kind of dyeing implementation. In the process of Dfs, we try to dye all points belonging to the same strongly connected component into one color, then the same color points are equivalent to one point. For example, after the reduction point in the example diagram just now, it can be like this:
A directed band ring graph is transformed into a directed acyclic graph (DAG graph). Many algorithms based on directed acyclic graphs need to use Tarjan algorithm to achieve dyeing shrinkage points, build a DAG graph and then process the algorithm. In this case, Tarjan algorithm has a great use!
Then, we introduce an array color [i] to represent the color of node i, and an array stack [to implement a stack]. Then, in the process of Dfs, every point we encounter will be put on the stack, every time we encounter a key point, the elements in the stack will pop up until the top of the stack is the key point. So far, the pop-up elements can be dyed.
1 void Tarjan(int u)//This code is for reference only. 2 { 3 vis[u]=1; 4 low[u]=dfn[u]=cnt++; 5 stack[++tt]=u; 6 for(int i=0;i<mp[u].size();i++) 7 { 8 int v=mp[u][i]; 9 if(vis[v]==0)Tarjan(v); 10 if(vis[v]==1)low[u]=min(low[u],low[v]); 11 } 12 if(dfn[u]==low[u]) 13 { 14 sig++; 15 do 16 { 17 low[stack[tt]]=sig; 18 color[stack[tt]]=sig; 19 vis[stack[tt]]=-1; 20 } 21 while(stack[tt--]!=u); 22 } 23 }
Original: https://blog.csdn.net/justlovetao/article/details/6673602
Tarjan Algorithms for Strongly Connected Components of Directed Graphs [Strongly Connected Components of Directed Graphs]
In directed graph G, if there is at least one path between two vertices, the two vertices are strongly connected. If every two vertices of a digraph G are strongly connected, G is said to be a strongly connected graph. The maximally strongly connected subgraph of a digraph of a Non-Strongly connected graph is called a strongly connected component.
In the following graph, the subgraph {1,2,3,4} is a strongly connected component because vertices 1,2,3,4 are reachable in pairs. {5} and {6} are also two strongly connected components.
According to the definition, strong connected components are obtained by two-way traversal intersection method. The time complexity is O(N^2+M). The better method is Kosaraju algorithm or Tarjan algorithm, both of which have O(N+M) time complexity. This paper introduces the Tarjan algorithm. [Tarjan algorithm]
Tarjan algorithm is based on graph depth-first search algorithm, each strongly connected component is a sub-tree in the search tree. When searching, the unhandled nodes in the current search tree are added to a stack. When tracing back, we can judge whether the node from the top of the stack to the stack is a strongly connected component.
DFN(u) is defined as the sequence number (timestamp) of the node u search, and Low(u) is the sequence number of the earliest node in the stack that can be traced by the subtree of u or U. By definition,
1 Low(u)=Min
2 {
3 DFN(u),
4 Low (v), (u, v) is the branch edge, u is the parent node of V
5 DFN (v), (u, v) is the backward side (non-crossed side) pointing to the node in the stack.
6 }
When DFN(u)=Low(u), all nodes in the search subtree rooted by u are strongly connected components.
The pseudocode of the algorithm is as follows
1 tarjan(u) 2 { 3 DFN[u]=Low[u]=++Index // For nodes u Set the sequence number and Low initial value 4 Stack.push(u) // Will node u Press into the stack 5 for each (u, v) in E // Enumerate each side 6 if (v is not visted) // If the node v Not visited 7 tarjan(v) // Keep looking down 8 Low[u] = min(Low[u], Low[v]) 9 else if (v in S) // If the node v Still on the stack 10 Low[u] = min(Low[u], DFN[v]) 11 if (DFN[u] == Low[u]) // If the node u Is the root of strongly connected components 12 repeat 13 v = S.pop // take v Unstack, a vertex in the strongly connected component 14 print v 15 until (u== v) 16 }
Next is a demonstration of the algorithm flow.
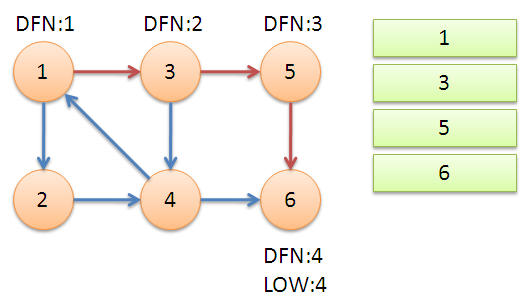
Starting from node 1, DFS adds the traversed nodes to the stack. When the node u=6 is searched, DFN[6]=LOW[6], a strongly connected component is found. Unstack until u=v, {6} is a strongly connected component.
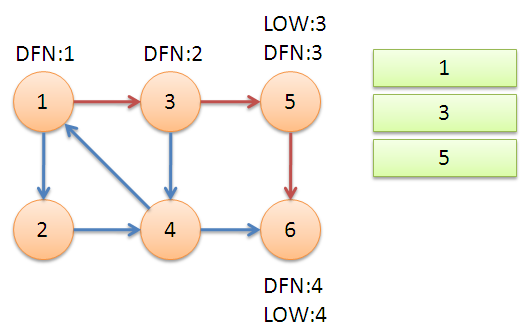
Returning to node 5, we find that DFN[5]=LOW[5], and {5} is a strongly connected component after de-stacking.
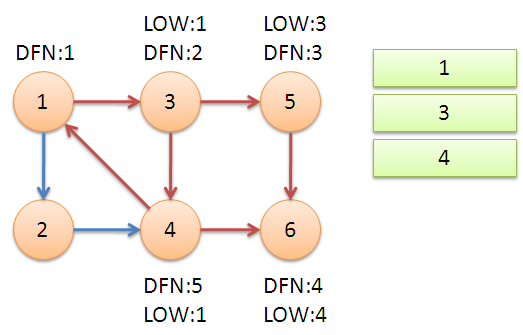
Return to Node 3, continue searching for Node 4, and add 4 to the stack. It is found that node 4 has a backward edge to node 1, and node 1 is still on the stack, so LOW[4]=1. Node 6 is out of the stack, (4,6) is a crosswise fork, and returns to 3, (3,4) is a branch, so LOW[3]=LOW[4]=1.
Go back to Node 1 and finally access Node 2. Access edges (2,4), 4 are still on the stack, so LOW[2]=DFN[4]=5. After returning to 1, it is found that DFN[1]=LOW[1], and all the nodes in the stack are taken out to form a connected component {1,3,4,2}.
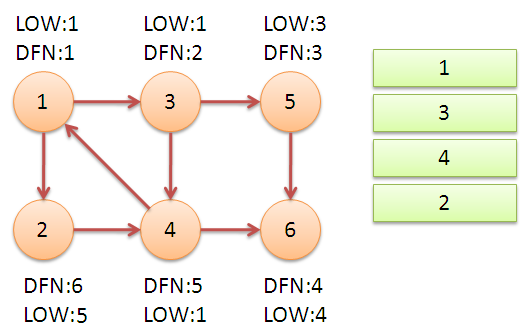
So far, the algorithm is over. Through this algorithm, all three strongly connected components {1,3,4,2}, {5}, {6} in the graph are obtained.
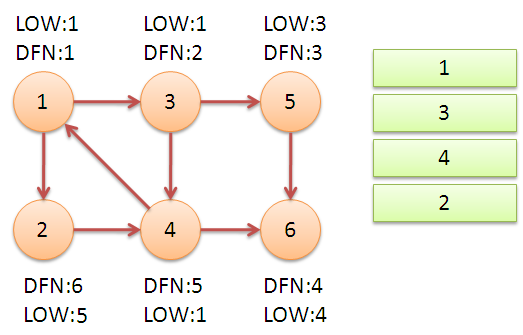
It can be found that in the process of running Tarjan algorithm, every vertex is visited once, and only once in and out of the stack, and every edge is visited only once, so the time complexity of the algorithm is O(N+M).
There is also a powerful algorithm for finding strongly connected components of digraphs, Kosaraju algorithm. Kosaraju is based on two DFS for digraphs and their inverses, and its time complexity is O(N+M). Compared with Trajan algorithm, Kosaraju algorithm may be slightly more intuitive. But Tarjan only uses DFS to the original graph once, and does not need to build the inverse graph, which is more concise. In the actual test, Tarjan algorithm is also about 30% more efficient than Kosaraju algorithm. In addition, the Tarjan algorithm is also closely related to the Tarjan algorithm for finding the bi-connected components (cut points and bridges) of undirected graphs. Learning the Tarjan algorithm is also helpful to understand the Tarjan algorithm for finding two connected components, which can be analogized and combined.
The Tarjan algorithm for finding strongly connected components of digraphs is named after its inventor Robert Tarjan. Robert Tarjan also invented the Tarjan algorithm for finding connected components, and the off-line Tarjan algorithm for finding the nearest common ancestor. Here, Tarjan is highly respected.
Attachment: C++ program of tarjan algorithm
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 #define N 100 6 #define M 100 7 struct Edge 8 { 9 int v; 10 int next; 11 }; 12 Edge edge[M];//Set of Edges 13 14 int node[N];//Vertex set 15 int instack[N];//Whether the marker is stack in 16 int stack[N]; 17 int Belong[N];//Which strongly connected component does each vertex belong to? 18 int DFN[N];//node u Search Number(time stamp) 19 int LOW[N];//u or u The sequence number of the earliest node in the stack traceable to the subtree(time stamp) 20 int n, m;//n: Number of points; m: Number of edges 21 int cnt_edge;//Side counter 22 int Index;//Serial number(time stamp) 23 int top; 24 int Bcnt;//How many strongly connected components are there 25 26 void add_edge(int u, int v)//Adjacent table storage 27 { 28 edge[cnt_edge].next = node[u]; 29 edge[cnt_edge].v = v; 30 node[u] = cnt_edge++; 31 } 32 void tarjan(int u) 33 { 34 int i,j; 35 int v; 36 DFN[u]=LOW[u]=++Index; 37 instack[u]=true; 38 stack[++top]=u; 39 for (i = node[u]; i != -1; i = edge[i].next) 40 { 41 v=edge[i].v; 42 if (!DFN[v])//If point v Not visited 43 { 44 tarjan(v); 45 if (LOW[v]<LOW[u]) 46 LOW[u]=LOW[v]; 47 } 48 else//If point v Has been visited 49 if (instack[v] && DFN[v]<LOW[u]) 50 LOW[u]=DFN[v]; 51 } 52 if (DFN[u]==LOW[u]) 53 { 54 Bcnt++; 55 do 56 { 57 j=stack[top--]; 58 instack[j]=false; 59 Belong[j]=Bcnt; 60 } 61 while (j!=u); 62 } 63 } 64 void solve() 65 { 66 int i; 67 top=Bcnt=Index=0; 68 memset(DFN,0,sizeof(DFN)); 69 memset(LOW,0,sizeof(LOW)); 70 for (i=1;i<=n;i++) 71 if (!DFN[i]) 72 tarjan(i); 73 } 74 int main() 75 { 76 freopen("in.txt","r",stdin); 77 int i,j,k; 78 cnt_edge=0; 79 memset(node,-1,sizeof(node)); 80 scanf("%d%d",&n,&m); 81 for(i=1;i<=m;i++) 82 { 83 scanf("%d%d",&j,&k); 84 add_edge(j,k); 85 } 86 solve(); 87 for(i=1;i<=n;i++) 88 printf("%d ",Belong[i]); 89 } 90
I write my own template for my use (negligible)
1 #include <stdio.h> 2 #include <string.h> 3 #include <algorithm> 4 #include <stack> 5 using namespace std; 6 #define N 100 7 #define M 100 8 9 struct Edge{ 10 int v; 11 int next; 12 }Edge[M];//Set of Edges 13 14 int node[N];//Vertex set 15 int instack[N];//Whether the marker is stack in 16 int Belong[N];//Which strongly connected component does each vertex belong to? 17 int DFN[N];//node u Search Number(time stamp) 18 int LOW[N];//u or u The sequence number of the earliest node in the stack traceable to the subtree(time stamp) 19 int n,m;//n: Number of points; m: Number of edges 20 int cnt_edge;//Side counter 21 int Index;//Serial number(time stamp) 22 int Bcnt; //How many strongly connected components are there 23 stack<int> sk; 24 25 void add_edge(int u,int v)//Adjacent table storage 26 { 27 Edge[cnt_edge].next=node[u]; 28 Edge[cnt_edge].v=v; 29 node[u]=cnt_edge++; 30 } 31 32 void tarjan(int u) 33 { 34 DFN[u]=LOW[u]=++Index; 35 instack[u]=1; 36 sk.push(u); 37 for(int i=node[u];i!=-1;i=Edge[i].next) 38 { 39 int v=Edge[i].v; 40 if(!DFN[v])//If point v Not visited 41 { 42 tarjan(v); 43 LOW[u]=min(LOW[u],LOW[v]); 44 } 45 else //If point v Has been visited 46 { 47 if(instack[v]&&DFN[v]<LOW[u]) 48 LOW[u]=DFN[v]; 49 } 50 } 51 if(DFN[u]==LOW[u]) 52 { 53 Bcnt++; 54 int t; 55 do{ 56 t=sk.top(); 57 sk.pop(); 58 instack[t]=0; 59 Belong[t]=Bcnt; 60 }while(t!=u); 61 } 62 } 63 64 int main() 65 { 66 freopen("sample.txt","r",stdin); 67 memset(node,-1,sizeof(node)); 68 scanf("%d %d",&n,&m); 69 for(int i=1;i<=m;i++) 70 { 71 int a,b; 72 scanf("%d %d",&a,&b); 73 add_edge(a,b); 74 } 75 for(int i=1;i<=n;i++) 76 { 77 if(!DFN[i]) 78 { 79 tarjan(i); 80 } 81 } 82 for(int i=1;i<=n;i++) 83 { 84 printf("%d ",Belong[i]); 85 } 86 return 0; 87 }
Network of Schools
http://poj.org/problem?id=1236
Description
A number of schools are connected to a computer network. Agreements have been developed among those schools: each school maintains a list of schools to which it distributes software (the "receiving schools"). Note that if B is in the distribution list of school A, then A does not necessarily appear in the list of school B
You are to write a program that computes the minimal number of schools that must receive a copy of the new software in order for the software to reach all schools in the network according to the agreement (Subtask A). As a further task, we want to ensure that by sending the copy of new software to an arbitrary school, this software will reach all schools in the network. To achieve this goal we may have to extend the lists of receivers by new members. Compute the minimal number of extensions that have to be made so that whatever school we send the new software to, it will reach all other schools (Subtask B). One extension means introducing one new member into the list of receivers of one school.
Input
The first line contains an integer N: the number of schools in the network (2 <= N <= 100). The schools are identified by the first N positive integers. Each of the next N lines describes a list of receivers. The line i+1 contains the identifiers of the receivers of school i. Each list ends with a 0. An empty list contains a 0 alone in the line.
Output
Your program should write two lines to the standard output. The first line should contain one positive integer: the solution of subtask A. The second line should contain the solution of subtask B.
Sample Input
5 2 4 3 0 4 5 0 0 0 1 0
Sample Output
1 2
Main idea: Give you a digraph and find out at least a few points, so that the whole graph can be them and their sub-nodes. The original graph can be transformed into a strongly connected graph by finding at least a few edges.
Solution: This question needs a little thought. After calculating strongly connected components and reducing points, there are a points with degree 0 and B points with degree zero. Then ans1=a, ans2 = max(a,b). In other special cases, when there is a strong connected component, ans2=0.
We can first reduce the point to get the dag map, and then we consider the first problem, to find that at least a few sets of software can be fully covered, the first topic has been guaranteed to be connected. Then we can think that if we put all the points into the software, it will be feasible. There must be some edges that will eventually get the software from the place where there must be an edge to distribute the software.
Then let's consider the second question. This is a connected graph. If we have some points without entry point, some points without exit point. If we try to connect the entry point with some exit points, we can ensure that we will eventually become many circles. In this way, the answer is the maximum value of the point without entry and the point without exit.
Question A: How many computers do we need in the network to make all schools have software? We can construct a DAG graph by using strong-connected algorithm contraction points. There must be a node with a penetration of 0 in the graph. Because this node can not transmit software through other nodes, we must put a computer in order to find the number of nodes with a penetration of 0.
Question B: How many lines should be added to the network at least, so that all schools can have software to place computers at any node. The answer is to find the maximum number of nodes with a degree of 0 and the number of nodes with a degree of 0.
Certificate B:
1. All the following points are isolated. When connecting two points, the starting edge connects the point with zero degree in the starting point and the point with zero degree in the ending point.
(1) Define that when the point n=1, if it is a point composed of a contraction point, it must add an anti-side, otherwise it does not need to add an edge.
(2) When the number of points n=2, join two points, condense into one point, and then according to the rule (1), the minimum number of added edges is 2.
(3) When n > 2, the minimum number of added edges can be obtained by shrinking the point through rule (2) and by rule (1) when the point is reduced to one.
2. Starting from the node with the nearest entrance of 0 and the node with the nearest exit of 0, all the points on the way including the starting point and the end point are condensed into one point, and all the edges connected with other nodes are disconnected. By this way, the DAG graph can be transformed into a graph composed of n (n > 0) outliers, and the minimum number of additional edges is determined to be the graph strongly connected. In general, one can get that the minimum number of added edges is n, because n outliers are all nodes with zero degree of entry, and the number of nodes with zero degree of output or two pairs form. It is known that n is the maximum number of nodes with zero degree of entry and the number of nodes with zero degree of output.
1 #include <stdio.h> 2 #include <iostream> 3 #include <string.h> 4 #include <algorithm> 5 #include <stack> 6 #include <string> 7 #include <sstream> 8 using namespace std; 9 const int maxn=1e6+5; // Can't be written#define maxn 1e6+5, compile errors 10 11 struct Edge{ 12 int v; 13 int next; 14 }Edge[maxn];//Set of Edges 15 16 int node[maxn];//Vertex set 17 int instack[maxn];//Whether the marker is stack in 18 int Belong[maxn];//Which strongly connected component does each vertex belong to? 19 int DFN[maxn];//node u Search Number(time stamp) 20 int LOW[maxn];//u or u The sequence number of the earliest node in the stack traceable to the subtree(time stamp) 21 int n,m;//n: Number of points; m: Number of edges 22 int cnt_edge;//Side counter 23 int Index;//Serial number(time stamp) 24 int Bcnt; //How many strongly connected components are there 25 int out[maxn];//Storage Output 26 int in[maxn];//Storage Degree 27 stack<int> sk; 28 29 void add_edge(int u,int v)//Adjacent table storage 30 { 31 Edge[cnt_edge].next=node[u]; 32 Edge[cnt_edge].v=v; 33 node[u]=cnt_edge++; 34 } 35 36 void tarjan(int u) 37 { 38 DFN[u]=LOW[u]=++Index; 39 instack[u]=1; 40 sk.push(u); 41 for(int i=node[u];i!=-1;i=Edge[i].next) 42 { 43 int v=Edge[i].v; 44 if(!DFN[v])//If point v Not visited 45 { 46 tarjan(v); 47 LOW[u]=min(LOW[u],LOW[v]); 48 } 49 else //If point v Has been visited 50 { 51 if(instack[v]&&DFN[v]<LOW[u]) 52 LOW[u]=DFN[v]; 53 } 54 } 55 if(DFN[u]==LOW[u]) 56 { 57 Bcnt++; 58 int t; 59 do{ 60 t=sk.top(); 61 sk.pop(); 62 instack[t]=0; 63 Belong[t]=Bcnt; 64 }while(t!=u); 65 } 66 } 67 68 void work() 69 { 70 for(int i=1;i<=n;i++) 71 { 72 for(int j=node[i];j!=-1;j=Edge[j].next) 73 { 74 int v=Edge[j].v; 75 if(Belong[i]!=Belong[v]) 76 { 77 out[Belong[i]]++; 78 in[Belong[v]]++; 79 } 80 } 81 } 82 int RU=0; 83 int CHU=0; 84 for(int i=1;i<=Bcnt;i++) 85 { 86 if(!in[i]) RU++; 87 if(!out[i]) CHU++; 88 } 89 if(Bcnt==1) 90 printf("1\n0\n"); 91 else 92 printf("%d\n%d\n",RU,max(RU,CHU)); 93 } 94 95 int main() 96 { 97 freopen("sample.txt","r",stdin); 98 memset(node,-1,sizeof(node)); 99 scanf("%d",&n); 100 getchar(); 101 for(int i=1;i<=n;i++) 102 { 103 int v; 104 string str; 105 getline(cin,str); 106 istringstream ss(str); 107 while(ss >> v&&v) 108 { 109 add_edge(i,v); 110 } 111 } 112 for(int i=1;i<=n;i++) 113 { 114 if(!DFN[i]) 115 { 116 tarjan(i); 117 } 118 } 119 work(); 120 return 0; 121 }