Before we talk about high-precision addition, subtraction, multiplication and division operations, let's first understand what high-precision operations are.

In fact, high accuracy means that the range of data and results involved in the operation is beyond the range of data size that standard data types can represent. At this time, if we want to get the correct calculation results, obviously we can not rely on the ordinary method to achieve. On the basis of general operation principle, auxiliary algorithm is used to realize the calculation of super-large data. For example, find the sum of two 100-bit data, or calculate the product of two 100-bit numbers. High-precision algorithms will be used at this time.

1. High Precision Addition

The principle of high precision addition:
1. Number of digits of calculation results
358934760892734899, a total of 18 digits
38960302975237462 with 17 digits
So the result will not exceed 19.

2. Divide the calculated numbers into segments and arrange them in order (here 0-32767 is the limit of the number stored in each storage unit). In order to improve the efficiency of space utilization, a storage unit can store multiple digits: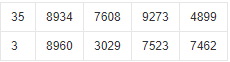

3. Add the two numbers together.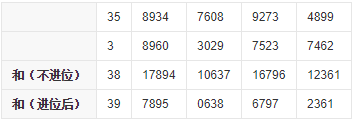

4. Output results.
Output from high to low. In addition to the highest position, the other low position less than 4 places should be added to the front 0.

The code is as follows:

#include <bits/stdc++/h>
using namespace std;  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],len;   //The size of the array determines the maximum number of digits with high accuracy.  
  int i;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;   //Enter two strings  
  a[0]=str1.length();  //Gets the length of the first string  
  for(i=1;i<=a[0];i++)  //Convert the first string to an integer and store it in array a  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();   //Gets the second string length  
  for(i=1;i<=b[0];i++)   //Convert each bit of the second string to an integer and store it in array B  
    b[i]=str2[b[0]-i]-'0';  
  len=(a[0]>b[0]?a[0]:b[0]);   //Take the maximum length of two strings  
  for(i=1;i<=len;i++)   //Do bitwise addition while processing carry  
  {  
    a[i]+=b[i];  
    a[i+1]+=a[i]/10;  
    a[i]%=10;     
  }  
  len++;    //The following is to remove the highest bit of 0, and then output.  
  while((a[len]==0)&&(len>1)) len--;  
  for(i=len;i>=1;i--)  
    cout<<a[i];  
  return 0;   
}  
   
//Note: When two numbers are added together, the number of digits in the result should be one more than the one larger in the two numbers. 

2. High Precision Subtraction:

The principle of high precision addition:
1. High-precision subtraction is slightly more complicated than high-precision addition because subtraction deals with more details when the difference is negative: when the subtraction is less than the subtraction, the difference is negative, and the absolute value of the difference is subtraction; in program implementation, one variable is used to store symbol bits and another array is used to store the difference. Absolute value.

2. Implementation process
(1) Compare size first

(2) Decide whether the output symbol is positive or negative

(3) Subtraction by position and attention should be paid to dealing with borrowings

The code is as follows:

#include <bits/stdc++.h>
using namespace std;  
int compare(string s1,string s2);  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],len;  
  int i;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;  
  a[0]=str1.length();  
  for(i=1;i<=a[0];i++)  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();  
  for(i=1;i<=b[0];i++)  
    b[i]=str2[b[0]-i]-'0';  
  if((compare(str1,str2))==0)  //If it is greater than or equal to, subtract by bit and deal with the debit.  
  {  
    for(i=1;i<=a[0];i++)  
      {a[i]-=b[i];  
       if (a[i]<0) {a[i+1]--;a[i]+=10;}  
      }  
    a[0]++;  
    while((a[a[0]]==0)&&(a[0]>1)) a[0]--;  
    for(i=a[0];i>=1;i--)  
      cout<<a[i];  
    cout<<endl;   
  }                            
  else  
  {  
    cout<<'-';  //Output minus sign when less than  
    for(i=1;i<=b[0];i++)  //Make a bit-by-bit reduction, a big reduction.  
      {b[i]-=a[i];  
       if (b[i]<0) {b[i+1]--;b[i]+=10;}  
      }  
    b[0]++;  
    while((b[b[0]]==0)&&(b[0]>1)) b[0]--;  
    for(i=b[0];i>=1;i--)  
      cout<<b[i];  
    cout<<endl;          
  }  
  return 0;   
}  
int compare(string s1,string s2)  //Compare the size of a string (two numbers) number, greater than or equal to return 0, less than return 1.  
{  
  if(s1.length()>s2.length()) return 0;  //Compare the length first, which string is long, the corresponding number is large.  
  if(s1.length()<s2.length()) return 1;  
  for(int i=0;i<=s1.length();i++)  //When the length is the same, compare one by one.  
  {  
    if(s1[i]>s2[i]) return 0;  
    if(s1[i]<s2[i]) return 1;                            
  }  
  return 0;   //If the length is the same and each bit is the same, return 0, indicating equality.  
}  

3. High Precision Multiplication:

Principle of High Precision Multiplication Implementation:
1. Because of the large number, it is impossible to use simple data structure to store the numbers. Arrays and strings are chosen to store the numbers. Strings facilitate our input of high-bit integers, while the simplicity of integer arrays is conducive to the calculation of each digit. Combining the advantages of both, high-precision multiplication can be achieved.

2. Implementation process
(1) Enter two integers through two strings

(2) Introduce two arrays and store each integer cut into the array.

(3) Operating for each person

(4) Processing carry

(5) Output results

The code is as follows:

#include <bits/stdc++.h>
using namespace std;  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],c[500],len;    //Multiplication of two numbers within 250 bits  
  int i,j;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;  
  a[0]=str1.length();  
  for(i=1;i<=a[0];i++)  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();  
  for(i=1;i<=b[0];i++)  
    b[i]=str2[b[0]-i]-'0';  
  memset(c,0,sizeof(c));  
  for(i=1;i<=a[0];i++)   //Do bit-by-bit multiplication and process carry at the same time. Pay attention to the writing of sentences in the loop.  
    for(j=1;j<=b[0];j++)  
    {  
    c[i+j-1]+=a[i]*b[j];  
    c[i+j]+=c[i+j-1]/10;  
    c[i+j-1]%=10;     
    }  
  len=a[0]+b[0]+1;  //Remove the highest bit of 0, and then output  
  while((c[len]==0)&&(len>1)) len--;   //Why do you want len > 1 here?  
  for(i=len;i>=1;i--)  
    cout<<c[i];  
  return 0;   
}  

4. High Precision Division:

High-precision division is a complex part, and its implementation principle can be divided into two situations:

In the first case:
Dividing high-precision by low-precision is actually dividing every dividend, including the remainder before it.

The code is as follows:

#include <bits/stdc++.h>
using namespace std;
int main()
{
    char a1[100],c1[100];
    int a[100],c[100],lena,i,x=0,lenc,b;
    memset(a,0,sizeof(a));
    memset(c,0,sizeof(c));
    gets(a1);  //Input High Precision Divisor 
    cin>>b;    //Input Low Precision Divisor 
    lena=strlen(a1);
    for (i=0;i<=lena-1;i++)
　　      a[i+1]=a1[i]-48;   //Put high-precision dividends into a array 
    for (i=1;i<=lena;i++)            //Division by phase
        {
            c[i]=(x*10+a[i])/b;
                x=(x*10+a[i])%b;
        }
　   lenc=1;
    while (c[lenc]==0&&lenc<lena) 
 　  lenc++;       //Delete Leader 0
    for (i=lenc;i<=lena;i++) 
    cout<<c[i];
    cout<<endl;
    return 0;
}

The second case: divide high precision by high precision.

The code is as follows:

#include <bits/stdc++.h>
using namespace std;
int a[100],b[100],c[100];
int compare(int a[],int b[])//Compare a and b, if a > b is 1; if a < B is - 1; if a=b is 0
{
    int i;
    if(a[0]>b[0])
        return 1;
    if(a[0]<b[0])
        return -1;
    for(i=a[0];i>0;i--)//Comparisons from high to low
    {
        if(a[i]>b[i])
            return 1;
        if(a[i]<b[i])
            return -1;
    }
    return 0;
}
 
void subduction(int a[],int b[])//Calculate a=a-b
{
    int flag;
    int i;
 
    flag=compare(a,b);
    if(flag==0)//Equal
    {
        a[0]=0;
        return;
    }
    if(flag==1)//greater than
    {
        for(i=1;i<=a[0];i++)
        {
            if(a[i]<b[i])//If it's not enough to borrow
            {
                a[i+1]--;
                a[i]+=10;
            }
            a[i]-=b[i];
        }
        while(a[0]>0&&a[a[0]]==0)//Delete Leader 0
            a[0]--;
        return;
    }
}
int main()
{
    char str1[100],str2[100];
    int i,j;
 
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c));
 
    cin>>str1>>str2;
    a[0]=strlen(str1);//a[0] The number of digits in the storage string 1
    b[0]=strlen(str2);//b[0] Bit of storage string 2
    for(i=1;i<=a[0];i++)
        a[i]=str1[a[0]-i]-'0';
    for(i=1;i<=b[0];i++)
        b[i]=str2[b[0]-i]-'0';
 
 
    int temp[100];
    c[0]=a[0]-b[0]+1;
    for(i=c[0];i>0;i--)
    {
        memset(temp,0,sizeof(temp));
 
        for(j=1;j<=b[0];j++)//From i, copy array b to array temp
            temp[j+i-1]=b[j];
        temp[0]=b[0]+i-1;
 
        while(compare(a,temp)>=0)//Subtraction simulation
        {
            c[i]++;
            subduction(a,temp);
        }
    }
 
    while(c[0]>0&&c[c[0]]==0)//Delete Leader 0
        c[0]--;
 
    cout<<"Shangwei:";
    if(c[0]==0)//Output results
        cout<<0<<endl;
    else
    {
        for(i=c[0];i>0;i--)
            cout<<c[i];
        cout<<endl;
    }
 
    cout<<"The remainder is:";
    if(a[0]==0)//Output Residual
        cout<<0<<endl;
    else
    {
        for(i=a[0];i>0;i--)
            cout<<a[i];
        cout<<endl;
    }
 
    return 0;
}