Title:

Topic link: LUOGU Long-necked Deer Placement
Explanation:
I just looked like a search. Then I went to search optimization, pruning, thinking about what A* was, and then I saw a sentence on the topic:

Then,,, (without words)
I changed my mind and wanted to build a map directly, but it was really not very good at it. I looked at the problem. I drew a picture according to the idea of parity. Here is sample 2. According to parity, we can build a whole picture (repeating the outline of the frame, and only drawing the first two lines).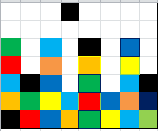

So just build edges directly according to parity, even sequence belongs to X set, odd sequence belongs to Y set (because even + odd = odd) so it must be a bipartite graph. After building the graph, we can find the maximum independent set of the bipartite graph, that is, all points - maximum matching.
(the first point I've been in T for a long time, the card is often serious, and I just started O2O_{2}O2.

Code:

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
	int s=0,w=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch<='9'&&ch>='0')s=s*10+ch-'0',ch=getchar();
	return s*w;
}
const int sea=220;
const int pool=50005;
int dx[8]={3,3,1,-1,-3,-3,1,-1};
int dy[8]={1,-1,3,3,1,-1,-3,-3};
int n,m,k,ans,a[sea][sea],v[pool],pre[pool];
int tot=0,last[pool];
struct see{int ver,next;}e[1000000];//Neighborhood tables are used here, but two-dimensional arrays cannot be saved. 
void add(int x,int y){e[++tot].next=last[x],e[tot].ver=y;last[x]=tot;}
int f(int x,int y){return (x-1)*m+y;}//Processing point mark 
bool hgry(int x)
{
	for(int i=last[x];i;i=e[i].next)
	{
		int y=e[i].ver;
		if(v[y]) continue; v[y]=1;
		if(!pre[y]||hgry(pre[y])){pre[y]=x;return 1;}
	}
	return 0;
}
int main()
{
	n=read(); m=read(); k=read();ans=n*m;
	for(int i=1;i<=k;i++)
	{
		int x=read(),y=read(); 
		a[x][y]=1;
	}
	memset(pre,0,sizeof(pre));
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
	if(i%2==0&&!a[i][j])//Edge building according to parity
	for(int k=0;k<8;k++)
	{
		int x=i+dx[k],y=j+dy[k];
		if(x<=n&&x>0&&y<=m&&y>0&&!a[x][y])
		 add(f(i,j),f(x,y));
	}
	// The maximum independent set can be obtained directly. 
	int s=0;
	for(int i=1;i<=f(n,m);i++)
	{
		memset(v,0,sizeof(v));
		if(hgry(i)) s++;
	}
	printf("%d\n",ans-s-k);//(Don't forget to subtract the points you can't put in)
	return 0;
}

Continue......