Portal

First of all, there is a 30 point method of violence. Let f[i][j] be or i, j probability.

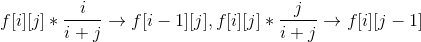
Then v[i] is the current sequence

Then you will find out that it's an isochromatic when type = 1, and a second-order isochromatic when type = 2.

That is to say, we only need to maintain the first three items, and then insert the last one violently.

Each time we divide into A and n - A piles, we need to insert the values of A+1,A+2, A+3, and then solve the current first three items similar to the above v

Now the only problem is the f array. Obviously, it can't be processed by n^2.

We found that the numerator and denominator are determined.

Denominator is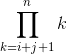

The molecule is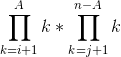

Then the two stacks are taken as a combination number.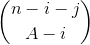

30 pts

#include<bits/stdc++.h>
#define N 105
using namespace std;
typedef long long ll;
int read(){
	int cnt = 0, f = 1; char ch = 0;
	while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1;}
	while(isdigit(ch)) cnt = (cnt << 1) + (cnt << 3) + (ch-'0'), ch = getchar();
	return cnt * f;
}
const int Mod = 998244353;
int n, m, type;
ll f[N][N], v[N], a[N], b[N];
ll add(ll a, ll b){ return (a+b) % Mod;}
ll mul(ll a, ll b){ return (a*b) % Mod;}
ll power(ll a, ll b){
	ll ans = 1;
	for(;b;b>>=1){
		if(b&1) ans = mul(ans, a);
		a = mul(a, a);
	} return ans;
}
int main(){
	n = read(), m = read(), type = read();
	for(int i=1; i<=n; i++) v[i] = (type == 1 ? i : mul(i, i));
	for(int Case=1; Case<=m; Case++){
		int A = read(); 
		for(int i=1; i<=A; i++) a[i] = v[i];
		for(int i=1; i<=n-A; i++) b[i] = v[i + A];
		memset(f, 0, sizeof(f));
		f[A][n-A] = 1;
		for(int i=A; i>=0; i--){
			for(int j=n-A; j>=0; j--){
				ll inv = power(i + j, Mod - 2);
				if(i) f[i-1][j] = add(f[i-1][j], mul(f[i][j], mul(inv, i)));
				if(j) f[i][j-1] = add(f[i][j-1], mul(f[i][j], mul(inv, j)));
			}
		} memset(v, 0, sizeof(v));
		for(int i=n; i>=1; i--){
			ll inv = power(i, Mod - 2);
			for(int j=min(i, A); j>=0; j--){
				int k = i - j; if(k > n - A) break;
				if(j) v[i] = add(v[i], mul(f[j][k], mul(a[j], mul(inv, j))));
				if(k) v[i] = add(v[i], mul(f[j][k], mul(b[k], mul(inv, k))));
			}
		}
	}
	int q = read();
	for(int i=1; i<=q; i++){
		int x = read(); printf("%lld\n", v[x]);
	} return 0;
}

100 pts

#include<bits/stdc++.h>
#define N 10000050
using namespace std;
typedef long long ll;
int read(){
	int cnt = 0, f = 1; char ch = 0;
	while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1;}
	while(isdigit(ch)) cnt = (cnt << 1) + (cnt << 3) + (ch-'0'), ch = getchar();
	return cnt * f;
}
const int Mod = 998244353;
int n, m, type;
ll add(ll a, ll b){ return (a+b) % Mod;}
ll mul(ll a, ll b){ return (a*b) % Mod;}
ll power(ll a, ll b){
	ll ans = 1;
	for(;b;b>>=1){
		if(b&1) ans = mul(ans, a);
		a = mul(a, a);
	} return ans;
}
ll fac[N], inv[N];
void prework(){
	fac[0] = fac[1] = inv[0] = inv[1] = 1;
	for(int i=2; i<=n; i++) fac[i] = mul(fac[i-1], i);
	inv[n] = power(fac[n], Mod - 2);
	for(int i=n-1; i>=2; i--) inv[i] = mul(inv[i+1], i+1);
}
ll f[5], g[5], h[5], pre[5], suf[5];
ll C(int n, int m){ return mul(fac[n], mul(inv[n-m], inv[m]));}
ll Get(int A, int B, int i, int j){
	if(A < i || B < j) return 0;
	ll ans = power(mul(fac[A + B], inv[i + j]), Mod - 2);
	ans = mul(ans, C(A + B - i - j, A - i));
	ans = mul(ans, mul(mul(fac[A], inv[i]), mul(fac[B], inv[j])));
	return ans;
}
const int up = 3;
ll lagrange(ll *y, int n){
	if(n <= up) return y[n]; pre[0] = suf[up + 1] = 1;
	for(int i=1; i<=up; i++) pre[i] = mul(pre[i-1], n - i);
	for(int i=up; i>=1; i--) suf[i] = mul(suf[i+1], n - i);
	ll ans = 0;
	for(int i=1; i<=up; i++){
		ll tmp = mul(y[i], mul(mul(inv[i-1], inv[up-i]), mul(pre[i-1], suf[i+1])));
		ans = ((up - i) & 1) ? add(ans, Mod - tmp) : add(ans, tmp);
	} return ans;
}
int main(){
	freopen("landlords.in","r",stdin);
	freopen("landlords.out","w",stdout);
	n = read(), m = read(), type = read(); prework();
	for(int i=1; i<=3; i++) f[i] = (type == 1 ? i : mul(i, i));
	for(int Case = 1; Case <= m; Case ++){
		int A = read();
		swap(f, g);
		for(int i=1; i<=3; i++) h[i] = lagrange(g, A + i);
		memset(f, 0, sizeof(f));
		for(int i=0; i<=3; i++){
			for(int j=0; i+j <= 3; j++){
				if(i + j == 0) continue;
				ll tmp = Get(A, n - A, i, j);
				ll inv = power(i + j, Mod - 2);
				f[i + j] = add(f[i + j], mul(tmp, mul(g[i], mul(i, inv))));
				f[i + j] = add(f[i + j], mul(tmp, mul(h[j], mul(j, inv))));
			}
		}
	}
	int q = read();
	while(q--){
		int x = read(); printf("%lld\n", lagrange(f, x));
	} return 0;
}