Leetcode525: continuous array
Title:
Method 1: change 0 to - 1, which is equivalent to finding the length of the maximum continuous subarray whose cumulative sum of continuous subarrays is 0, but this problem will have a boundary, only the length of the maximum continuous subarray is required to have a boundary, this is 0, - 1, but if I change to find the length of the maximum continuous subarray whose cumulative sum is 7, then the boundary is 7, - 1, that is to say, first, put (7, - 1 )Put it in the map
class Solution {
public int findMaxLength(int[] nums) {
//
for(int i=0;i<nums.length;i++){
if(nums[i]==0){
nums[i]=-1;
}
}
//Find the maximum subarray length with the sum of accumulation of 0
int cur=0;
Map<Integer,Integer> map=new HashMap();
map.put(0,-1);
int max=0;
for(int i=0;i<nums.length;i++){
cur+=nums[i];
if(map.containsKey(cur)){
max=Math.max(max,i-map.get(cur));
}else{
map.put(cur,i);
}
}
return max;
}
}
Method 2: use a help array to record the quantity of 0 and 1. When arriving at a new position, update the quantity and calculate the difference value. If the difference value has appeared before, then the subscript subtraction is the result and update max. but pay attention to the boundary problem. The boundary of this problem is still the difference value = 0.
class Solution {
public int findMaxLength(int[] nums) {
Map<Integer,Integer> map=new HashMap();
int[] help=new int[2];
map.put(0,-1);//In the same way, this method also has boundary problems, that is, if the difference is 0, then it is the longest from beginning to end.
int max=0;
int cha=0;
for(int i=0;i<nums.length;i++){
int a=nums[i]==0?help[0]++:help[1]++;//This a is useless, mainly because I want to use Sanmu
cha=help[1]-help[0];
if(map.containsKey(cha)){
max=Math.max(max,i-map.get(cha));
}else{
map.put(cha,i);
}
}
return max;
}
}
The sum of leetcode 560 is the number of k continuous subarrays
Title: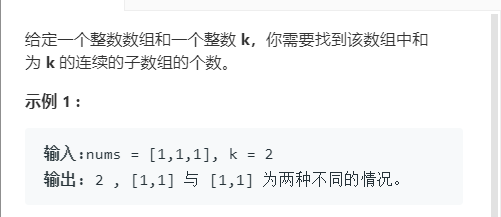
It is to calculate the prefix sum, and then see whether the current prefix and - k have appeared before. What is put in the map is the prefix sum and how many times the prefix sum has appeared. Note a boundary condition, that is, the prefix sum is 0. By default, it appears once, which is to calculate once by yourself.
class Solution {
public int subarraySum(int[] nums, int k) {
Map<Integer,Integer> map=new HashMap();
map.put(0,1);
int res=0;
int cur=0;
for(int i=0;i<nums.length;i++){
cur+=nums[i];
if(map.containsKey(cur-k)){
res+=map.get(cur-k);
}
map.put(cur,map.getOrDefault(cur,0)+1);
}
return res;
}
}
The elements of leetcode 1074 and the number of submatrixes for the target value (I finally made it by myself, but I didn't understand it by others... Food is the original sin)
Title:
Analysis: it is to compress the matrix information, and then turn it into a compressed matrix to find the number of continuous subarrays equal to k (it turns into the problem of leetcode 560, I'm really too smart), and the matrix information compression is too useful
class Solution {
public int numSubmatrixSumTarget(int[][] arr, int target) {
//I can also use a compressed matrix, but the function and matrix subsequence are different from the largest one. My matrix represents the sum of a row to this row, and then I traverse this matrix to compare with target.
if(arr==null||arr.length==0||arr[0].length==0){
return 0;
}
int res=0;//Number of non empty submatrixes, initially 0
for(int i=0;i<arr.length;i++){
int[] temp=new int[arr[0].length];
for(int j=i;j<arr.length;j++){
Map<Integer,Integer> map=new HashMap();
map.put(0,1);
int cur=0;
for(int k=0;k<arr[0].length;k++){
temp[k]=temp[k]+arr[j][k];
cur+=temp[k];
if(map.containsKey(cur-target)){
res+=map.get(cur-target);
}
map.put(cur,map.getOrDefault(cur,0)+1);
}
}
}
return res;
}
}
The largest subsequence of the product of leetcode 152
Title:
Method 1: violence enumeration, timeout
class Solution {
public int maxProduct(int[] nums) {
int max=Integer.MIN_VALUE;
for(int i=0;i<nums.length;i++){
for(int j=i;j<nums.length;j++){
int temp=1;
for(int k=j;k<nums.length;k++){
temp*=nums[k];
max=Math.max(max,temp);
}
}
}
return max;
}
}
Method 2: another way of thinking is to end with i. although it passes, it's slow. It's more than 5%. i'm curious about how that 5 percent of what is done...
class Solution {
public int maxProduct(int[] nums) {
int max=Integer.MIN_VALUE;
//Maximum cumulative product ending in i
for(int i=0;i<nums.length;i++){
int help=1;
int k=i;
while(k>=0){
help=help*nums[k];
max=Math.max(max,help);
k--;
}
}
return max;
}
}
Method 3: I started to think about recursion. Starting from the last bit, each step probably needs the maximum, minimum and result of the subsequence that the previous node ends. Write out the dynamic planning???
class Solution {
public int maxProduct(int[] nums) {
int max=Integer.MIN_VALUE;
//Change your mind, try the violent ground cabinet, so as to change the dynamic planning
int[] help=new int[2];
for(int i=0;i<nums.length;i++){
if(i==0){
help[0]=help[1]=nums[0];
max=Math.max(max,help[0]);
continue;
}
int temp1=help[0];//Maximum value
int temp2=help[1];//minimum value
help[0]=Math.max(nums[i],Math.max(temp1*nums[i],temp2*nums[i]));
help[1]=Math.min(nums[i],Math.min(temp1*nums[i],temp2*nums[i]));
max=Math.max(max,help[0]);
}
return max;
}
}