Title address

Learn from the big guy's blog: https://www.cnblogs.com/AK-ls/p/10509986.html

Title Description

Recently, little C has learned many algorithms of minimum spanning tree, such as Prim algorithm, Kurskal algorithm, loop elimination algorithm, etc. Just when little C is complacent, little p pours cold water on little c again. According to small P, let small C find a sub small spanning tree of undirected graph, and this sub small spanning tree must be strictly sub small, that is to say, if the edge set selected by the minimum spanning tree is em and the edge set selected by the strict sub small spanning tree is ES, then it needs to meet the following requirements: (value(e) indicates the weight of edge e) ∑ e ∈ EM value(e) < Σ e ∈ ES value(e)
Now little C Meng has found you. I hope you can help him solve this problem.

Outline of thought

1. Find the minimum production tree first
2. Then enumerate all the edges val that are not on the tree and add them to the tree to form a ring. Find the largest edge val 1 and the second largest edge val 2 in the ring.
- if Val > val1, sum + val - val1 is a candidate answer
- if val = val1, sum + val - val2 is a candidate answer
3. How to find val1 and val2? It is necessary to use LCA multiplication to maintain dis1 [i] [J] to represent the value from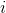Jump up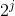Maximum edge between times, dis2 [i] [J] means from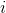Jump up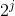The next largest edge between times (less than the largest edge)

fa[i][j] = fa[fa[i][j-1]][j-1];
dis1[i][j] = max(dis1[i][j-1], dis1[fa[i][j-1]][j-1]);        
if(dis1[i][j-1] == dis1[fa[i][j-1]][j-1])                        
    dis2[i][j] = max(dis2[i][j-1], dis2[fa[i][j-1]][j-1]);
else if(dis1[i][j-1] < dis1[fa[i][j-1]][j-1])
    dis2[i][j] = max(dis1[i][j-1], dis2[fa[i][j-1]][j-1]);
else
    dis2[i][j] = max(dis2[i][j-1], dis1[fa[i][j-1]][j-1]);    

Note: the data of this problem is very large, and the edge weight and long long to open.

AC code

 

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
using namespace std;
typedef long long ll;
const int maxn = 5e5+10;
const int inf = 1e9+7;
int fa[maxn][22], pre[maxn], vis[maxn], deep[maxn], cnt,dis1[maxn][22], dis2[maxn][22];
int n, m, head[maxn];
struct Tree{
    int u, v, w;
}t[maxn];

struct Edge{
    int v, next, w;
}e[maxn*2];

void add(int u, int v, int w){
    e[++cnt].v = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt;
}

int Find(int x){
    return x == pre[x] ? x:pre[x]=Find(pre[x]);
}

bool cmp(Tree a, Tree b){
    return a.w < b.w;
}

ll Kruskal(){    
    ll ans = 0;
    int num = 0;
    for(int i = 1; i <= m; i++){    
         int u = Find(t[i].u);
         int v = Find(t[i].v);
         if(u != v){
              pre[v] = u;
              ans += t[i].w*1ll;
              num++;
              add(t[i].u, t[i].v, t[i].w);
              add(t[i].v, t[i].u, t[i].w);
              vis[i] = 1;     
         }
         if(num == n-1)
            break;
    }
    return num == n-1?ans:-1;
}

void dfs(int u, int d){
    deep[u] = d;
    for(int i = head[u]; ~i; i = e[i].next){
        int v = e[i].v;
        if(fa[v][0]) continue;
        fa[v][0] = u;
        dis1[v][0] = e[i].w;
        dis2[v][0] = -inf;
        dfs(v, d+1);
    }
}

void update(){
    for(int j = 1;j <= 20; j++){
        for(int i = 1; i <= n; i++){
            fa[i][j] = fa[fa[i][j-1]][j-1];
            dis1[i][j] = max(dis1[i][j-1], dis1[fa[i][j-1]][j-1]);
            if(dis1[i][j-1] == dis1[fa[i][j-1]][j-1])
                dis2[i][j] = max(dis2[i][j-1], dis2[fa[i][j-1]][j-1]);
            else if(dis1[i][j-1] < dis1[fa[i][j-1]][j-1])
                dis2[i][j] = max(dis1[i][j-1], dis2[fa[i][j-1]][j-1]);
            else
                dis2[i][j] = max(dis2[i][j-1], dis1[fa[i][j-1]][j-1]);
        }
    }
}


int lca(int u, int v){
    if(deep[u] < deep[v])
        swap(u, v);
    int f = deep[u] - deep[v];
    for(int i = 0; (1<<i) <= f; i++){
        if(f & (1<<i)){
            u = fa[u][i];
        }
    }
    if(u != v){
        for(int i = 20; i >= 0; i--){
            if(fa[u][i] != fa[v][i]){
                u = fa[u][i];
                v = fa[v][i];
            }
        }
        u = fa[u][0];
    }
    return u;
}
int cal(int u, int f, int w){
    int v1, v2;
    v1 = v2 = -inf;
    int len = deep[u] - deep[f];
    for(int i = 0; (1<<i) <= len; i++){
        if(len & (1<<i)){
            v1 = max(dis1[u][i], v1);
            if(dis1[u][i] != v1)
                v2 = max(v2, dis1[u][i]);
            v2 = max(v2, dis2[u][i]);
            u = fa[u][i];
        }
    }
    if(v1 == w) return w - v2;
    else  return w - v1;
}
int main(){
    while(scanf("%d%d", &n, &m)!=EOF){
        int u, v, w;
        cnt = 0;
        memset(fa, 0, sizeof(fa));
        memset(head, -1, sizeof(head));
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= n; i++){
            pre[i] = i;
        }
        for(int i = 1; i <= m; i++){
            scanf("%d%d%d", &t[i].u, &t[i].v, &t[i].w);
        }
        sort(t+1, t+1+m, cmp);
        ll sum = Kruskal();
        fa[1][0] = 1;
        dfs(1, 1);
        update();
        int Min = inf;
        for(int i = 1; i <= m; i++){
            if(!vis[i]){
                int f = lca(t[i].u, t[i].v);
                Min = min(cal(t[i].u, f, t[i].w), Min);
                Min = min(cal(t[i].v, f, t[i].w), Min);
            }
        }
        printf("%lld\n", sum*1ll + Min*1ll);
    }
    return 0;
}