1. Deep traverse DFS
Similar to the first root traversal of a tree
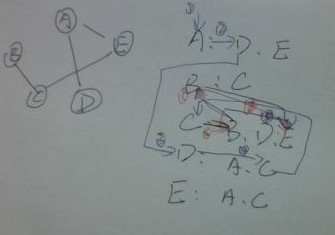
As shown in the figure, the depth traversal output of the above figure is ADCBE
The adjacency matrix of a graph is given. The graph is searched for depth first, starting from vertex 0
class Graph
{
private:
int flag[N];//State array
int Vexnum;//The number of vertices of a graph
int Matrix[N][N]; //adjacency matrix
void DFS(int v);
public:
Graph()
{
for(int i=0;i<N;i++)
flag[i]=0;
}
void DFStra();
void SetMatrix(int n,int p[N][N]);
}
void Graph::SetMatrix(int n,int p[N][N])//Set adjacency matrix
{
Vexnum=n;
for(int i=0;i<Vexnum;i++)
for(int j=0;j<Vexnum;j++)
{
Matrix[i][j]=p[i][j];
}
}
void Graph::DFStra()
{
int i;
for(i=0;i<Vexnum;i++)//There may be multiple connected graphs
{
if(flag[i]==0)//Found a vertex with state 0
DFS(i);
}
cout<<endl;
}
void Graph::DFS(int v)
{
int w,i,k;
flag[v]=1;//Set the state of this vertex to 1
cout<<v<<" ";
int temp[N];
for(i=0;i<Vexnum;i++)
temp[i]=0;
k=0;
for(i=0;i<Vexnum;i++)Find the vertex connected to the current vertex, and save temp Array
{
if(Matrix[v][i]==1)
temp[k++]=i;
}
i=0;
for(i=0;i<k;i++)//Recursively traversing these vertices
{
w=temp[i];
if(flag[w]==0)
DFS(w);
}
}
int main()
{
int t,i,num,j;
int x[N][N];
int n;
cin>>t;
while(t--)
{
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>x[i][j];
Graph p;
p.SetMatrix(n,x);
p.DFStra();
}
}
The test data are:
sample input
2
4
0 0 1 1
0 0 1 1
1 1 0 1
1 1 1 0
5
0 0 0 1 1
0 0 1 0 0
0 1 0 1 1
1 0 1 0 0
1 0 1 0 0
sample output
0 2 1 3
0 3 2 1 4
2. Breadth traversal BFS and calculation of the number of connected components
Breadth traversal is similar to tree level traversal
For example, a connection matrix is as follows
0 1 1 0 0 0 0 0
1 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 1 0
0 0 0 0 1 0 0 0
0 0 0 0 1 0 0 0
0 0 0 1 0 0 0 0
The matrix is illustrated as follows
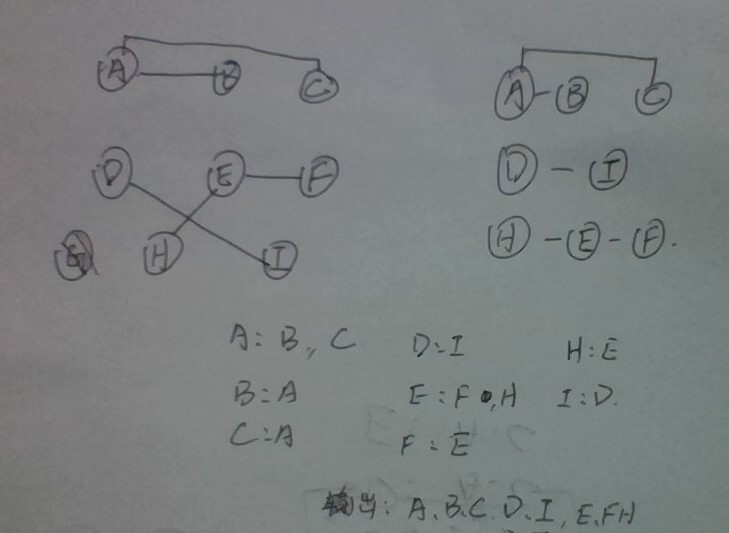
It can be seen that the connected component is 3, and the output through breadth traversal is ABCDIEFH
#include<bits/stdc++.h>
using namespace std ;
#define N 20
class Graph
{
private:
int flag[N];
int num;//Number of connected components
int Vexnum;
string temp[N];
int Matrix[N][N]; //Edge array
void BFS(int v);
public:
void BFStra() ;
Graph(string x[],int n) {
int i;
num=0;
Vexnum=n;
for(i=0;i<Vexnum;i++)
temp[i]=x[i];
for(int i=0;i<N;i++)
flag[i]=0;
for(int i=0;i<Vexnum;i++)
for(int j=0;j<Vexnum;j++)
{
Matrix[i][j]=0;
}
}
int find(string x);
void SetMatrix();
void display();
void GetNum();
};
void Graph::SetMatrix()//Initialize adjacency matrix
{
int i,k,j,x,y,h;
string a,b;
cin>>k;
i=0;
while(k--)
{
cin>>a>>b;
x=find(a);
y=find(b);
Matrix[x][y]=1;
Matrix[y][x]=1;
}
}
void Graph::BFStra()
{
int i=0;
for(i=0;i<Vexnum;i++)
if(flag[i]==0)
{
BFS(i);
}
}
void Graph::BFS(int v)
{
int w,u;
int i,k;
int temp[N];
queue<int> p;
k=0;
for(i=0;i<Vexnum;i++)
flag[i]=0;
for(v=0;v<Vexnum;v++)
{
if(flag[v]==0)
{ num++;
flag[v]=1;
cout<<v<<" ";
p.push(v); //Put the vertices that meet the requirements into the queue
while(!p.empty())
{
k=0;
u=p.front();
if(flag[u]==0)
{
cout<<u<<" ";
flag[u]=1;
}
p.pop();
for(i=0;i<Vexnum;i++)//Find vertices connected to the current vertex
{
if(Matrix[u][i]==1&&flag[i]==0)
{
p.push(i);
}
}
}
}
}
cout<<endl;
}
int Graph::find(string x)
{
for(int i=0;i<Vexnum;i++)
if(x==temp[i])
return i;
}
void Graph::display()
{
int i,j;
for(i=0;i<Vexnum;i++)
{
if(i!=0)
cout<<" ";
cout<<temp[i];
}
cout<<endl;
for(i=0;i<Vexnum;i++)
{
for(j=0;j<Vexnum;j++)
{
if(j!=0)
cout<<" ";
cout<<Matrix[i][j];
}
cout<<endl;
}
cout<<num<<endl;
}
int main()
{
int t,i,j;
string x[N];
int n;
cin>>t;
while(t--)
{
cin>>n;
for(i=0;i<n;i++)
cin>>x[i];
Graph p(x,n);
p.SetMatrix();
cout<<"Breadth traversal results:" <<endl;
p.BFStra();
cout<<endl;
p.display();
cout<<endl;
}
}