Because in the data structure, stack and queue look too similar. It is inevitable to compare them. Stack first in first out, queue first in first out. In the same way, it can only be operated at one end. When the problem arises, it can be realized by each other??
Can we have a good analysis? If we use two stacks to implement the queue, it seems that this operation is OK. Just give me a diagram and you'll see!

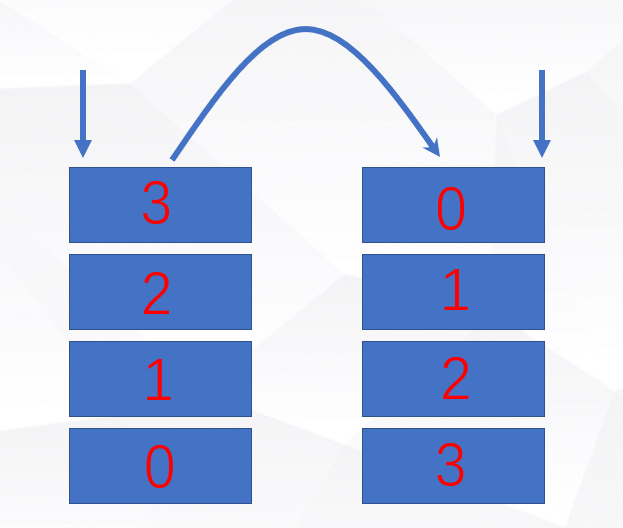
Obviously, two stacks can be used to realize the function of queue, that is, to transit through another stack. Such operation will also be used in dijkstra shortest path in graph theory algorithm. Convert LIFO to FIFO. So how to implement it in code? Since we need two stacks, we need to define two stacks. One is used for incoming queue operation and the other is used for outgoing queue operation. It's a perfect solution! The specific stacks and queues used have been implemented in the previous article, just use them. Of course, chained stacks and queues are the best.

Pay attention to the details when implementing. Don't say much, code:

#include "LinkStack.h"

template <typename T>
class StackToQueue
{
protected:
	mutable LinkStack<T> in_stack;	// Consider const objects
	mutable LinkStack<T> out_stack;
public:
	void enqueue(const T& obj)
	{
		in_stack.push(obj);	// Just join the team and press the stack
	}
	
	void dequeue()	// The details should be paid attention to when leaving the team
	{
		if( out_stack.size() == 0 )	// If the outbound stack is empty
		{				// Then the elements in the queue are transferred to the stack out of the queue
			while( in_stack.size() > 0 )
			{
				out_stack.push(in_stack.top());
				in_stack.pop();
			}
			
			out_stack.pop();	// Real outbound operation
		}
		else
		{
			out_stack.pop();	//If the stack out of the queue has elements, directly out of the queue
		}
	}

	T front() const		// The operation of getting team head element is basically the same as that of leaving the team
	{
		T ret;
		
		if( out_stack.size() == 0 )	// If the stack out of the queue is empty
		{				
			while( in_stack.size() > 0 )	// Then transfer the elements in the queue to the stack out of the queue
			{
				out_stack.push(in_stack.top());
				in_stack.pop();
			}
			
			ret = out_stack.top();	// Stack top element is team head element
		}
		else				// This is the case where the stack out of the queue is not empty
		{
			ret = out_stack.top();
		}
		
		return ret;
	}
	
	int length() const	// Add the sizes of the two stacks and return
	{
		return out_stack.size() + in_stack();
	}
	
	void clear()	// Empty two stacks
	{
		out_stack.clear();
		in_stack.clear();
	}
	
	~StackToQueue()
	{
		clear();
	}
};

To test whether the first in, first out of the queue is implemented, copy all the codes implemented above to the following test program, and I will omit this step

#include <iostream>

int main(int argc, const char* argv[])
{
	StackToQueue<int> queue;
	
	for(int i = 0; i < 10; ++ i)
	{
		queue.enqueue(i);
	}
	
	for(int i = 0; i < 10; ++ i)
	{
		cout << queue.front() << " ";
		queue.dequeue();
	}
	
	return 0;
}

OK, the stack implements the queue. How can the queue realize the stack? Let's look at the figure!

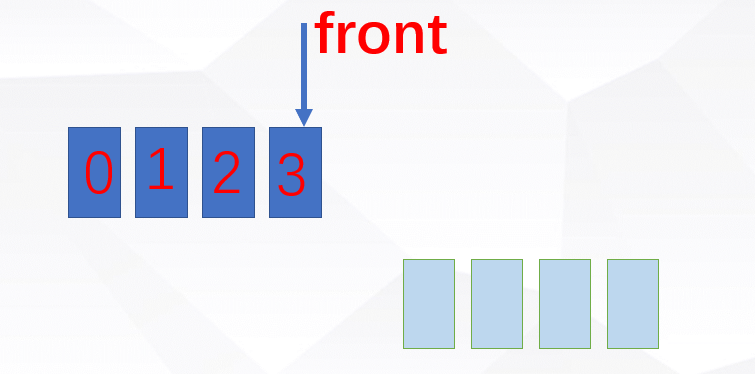
Use chestnut to explain ha. For example, in the figure above, one queue has four elements, and the other queue is empty. When entering the stack, the data will be directly put into the queue used as the input.

How to operate the stack? Take a look at the following figure:

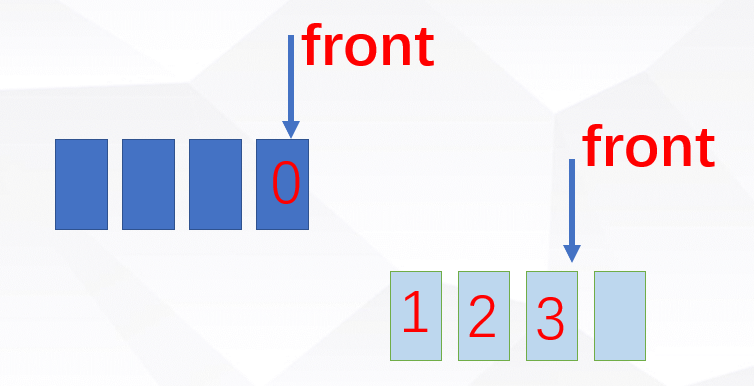
Transfer the n-1 elements of the first queue to another queue, and then find that there is only one element left in the first queue! Yes, then the location of this element is equivalent to the top of the stack. It's easy to get out of the stack. The first queue is finished. The same is true for getting the top element of the stack, except that the operation of getting out of the queue is replaced by getting the head element of the queue, and then returning it. But after the stack out operation, we must exchange the queue in and out of the stack, which is the key point of using the queue to realize the stack.

Now, it's time to code:

#include "LinkQueue.h"

template <typename T>
class QueueToStack
{
protected:
	mutable LinkQueue<T> queue1;
	mutable LinkQueue<T> queue2;
	mutable LinkQueue<T>* p_in;	// Exchange with pointer
	mutable LinkQueue<T>* p_out;	// More efficient
public:
	QueueToStack()			// Initialization pointer
	{
		p_in = &queue1;
		p_out = &queue2;
	}
	
	void push(const T& obj)		// Push operation
	{
		p_in->enqueue(obj);	// Direct to queue
	}
	
	void pop()			// Pay attention to stack out operation
	{
		if( p_in->length() >= 1 )	// If there are elements in the queue
		{
			while( p_in->length() > 1 )	// Then transfer n-1 elements to the outbound queue
			{
				p_out->enqueue(p_in->front());
				p_in->dequeue();
			}
			
			p_in->dequeue();	// After the transfer is completed, the queue in will be sent out, which is equivalent to the stack out
			
			LinkQueue<T>* tem = p_in;	// Exchange the points of two pointers as soon as the stack is out
			p_in = p_out;
			p_out = tem;
		}		
		else
		{
			throw(0);
		}
	}
	
	T top() const		// Get stack top element
	{
		T ret;
		
		if( p_in->length() >= 1 )	// It is almost the same as the stack exit operation, but does not need to exchange the pointer points
		{
			while( p_in->length() > 1 )
			{
				p_out->enqueue(p_in->front());
				p_in->dequeue();
			}
			
			ret = p_in->front();
		}									
		else
		{
			throw(0);
		}
		
		return ret;
	}
	
	int size() const
	{
		return p_in->length() + p_out->length();
	}
	
	void clear()
	{
		p_in->clear();
		p_out->clear();
	}
	
	~QueueToStack()
	{
		clear();
	}
};

Test whether the last in, first out of the stack is satisfied!

#include <iostream>

using namespace std;

int main(int argc, const char* argv[])
{
	QueueToStack<int> stack;

	for(int i = 0; i < 10; ++ i)
	{
		stack.push(i);
	}
	
	for(int i = 0; i < 10; ++ i)
	{
		cout << stack.top() << " ";
		stack.pop();
	}
	
	return 0;
}

Look at the output, satisfied!