Next larger element 1

Title Link

Maintain a monotonically decreasing stack, that is, when the traversal element is larger than the top element of the stack, save the result and pop up the top element of the stack
In order to get the results in the order of subset array 1, we need to use hash table to establish mapping relationship when operating array 2

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        stack<int> st;
        unordered_map<int,int> hash;
        for(int i=0;i<nums2.size();i++){
            while(!st.empty()&&nums2[i]>st.top()){
                hash[st.top()]=nums2[i];
                st.pop();
            }
            st.push(nums2[i]);
        }
        while(!st.empty()){
            hash[st.top()]=-1;
            st.pop();
        }
        vector<int> res;
        for(int i=0;i<nums1.size();i++){
            res.push_back(hash[nums1[i]]);
        }
        return res;
    }
};

Next maximum element 2

Title Link

Loop array, the processing method only needs to change the length of the array to twice, that is, to form a logically connected ring
Use remainder when traversing

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        int n=nums.size();
        vector<int> res(n,-1);
        stack<int> st;
        for(int i=0;i<n*2-1;i++){
            while(!st.empty()&&nums[i%n]>nums[st.top()]){
                res[st.top()]=nums[i%n];
                st.pop();
            }
            st.push(i%n);
        }
        return res;
    }
};

Daily temperature

Title Link

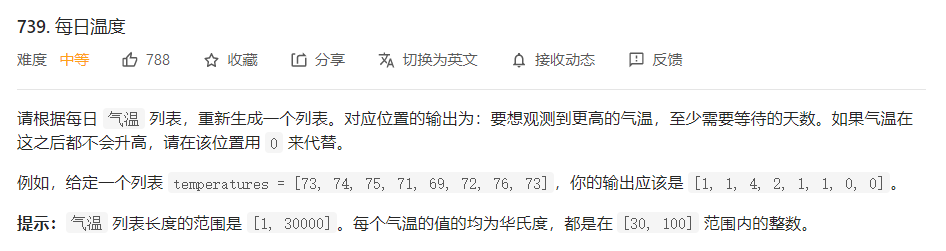
This question is the same as finding the next biggest element
We need to maintain a monotonically decreasing stack, that is, when the current traversal element is greater than the top element of the stack, save the result and pop up the top element of the stack

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        stack<int> st;
        vector<int> res(temperatures.size(),0);
        for(int i=0;i<temperatures.size();i++){
            while(!st.empty()&&temperatures[i]>temperatures[st.top()]){
                int tempd=st.top();
                st.pop();
                res[tempd]=i-tempd;
            }
            st.push(i);
        }
        return res;
    }
};

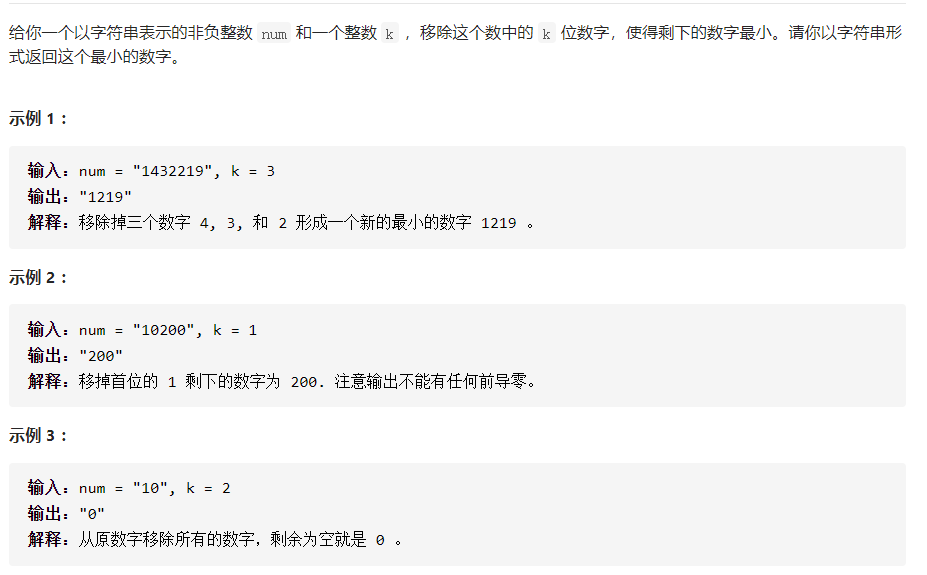
Remove K digits

Title Link

class Solution {
public:
    string removeKdigits(string num, int k) {
		stack<char> s;
		for (int i = 0; i < num.size(); i++)
		{
			while (!s.empty() && s.top() > num[i] && k)
			{
				s.pop();
				k--;
			}
			if (s.empty() && num[i] == '0')
				continue;//Skip leading 0
			s.push(num[i]);
		}
		string result;
		while (!s.empty())
		{
			if (k > 0)//When you need to remove the number again: delete the number from the top part of the monotonically increasing stack at this time
				k--;    //k> 0, it means that all elements of string enter the stack in the form of monotonic stack
	                    //(all string s are used up and monotonically increased, but k can still be deleted)
	                    //k is not used up. There must be all monotonous increments in the stack
	                    //So just pop out the large elements behind
			else if (k == 0)//When there is no need to remove numbers: take out the string to result
				result += s.top();
	
			s.pop();	
		}
		reverse(result.begin(), result.end());//reverse function in stl
		return result == "" ? "0" : result;
	}
};

Histogram Max rectangle

Title Link

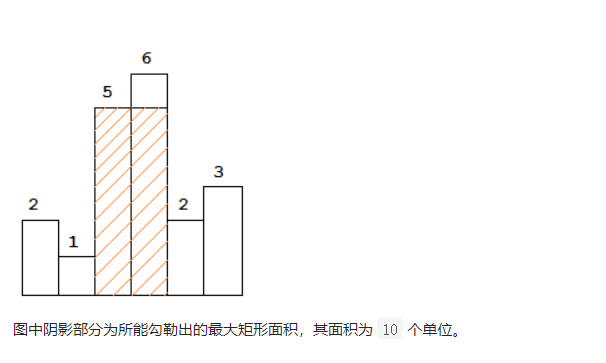
To find the boundary problem, the rectangular area is determined by the minimum height of the left and right sides
Therefore, maintain a monotonically increasing stack, that is, when the traversal element is smaller than the top element, it is necessary to calculate the rectangular area represented by the top element. The left boundary is the top element position, the right boundary is the current traversal position, and the height is the top value

• What this code pays attention to is that a 0 element is added to the ending element to represent the boundary of the ending element
  This can make the code simple. If you don't add it, you need a loop to calculate the rectangle represented by the remaining elements in the stack

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if(heights.size()==0) return 0;
        //if(heights.size()==1) return heights[0];
        heights.push_back(0);
        heights.insert(heights.begin(),0);
        stack<int> st;
        int maxArea=0;
        for(int i=0;i<heights.size();i++){
            while(!st.empty()&&heights[i]<heights[st.top()]){
                int h=heights[st.top()];
                st.pop();
                int width=i-st.top()-1;
                maxArea=max(maxArea,h*width);
            }
            st.push(i);
        }
        return maxArea;
    }
};

Receive rainwater

Title Link

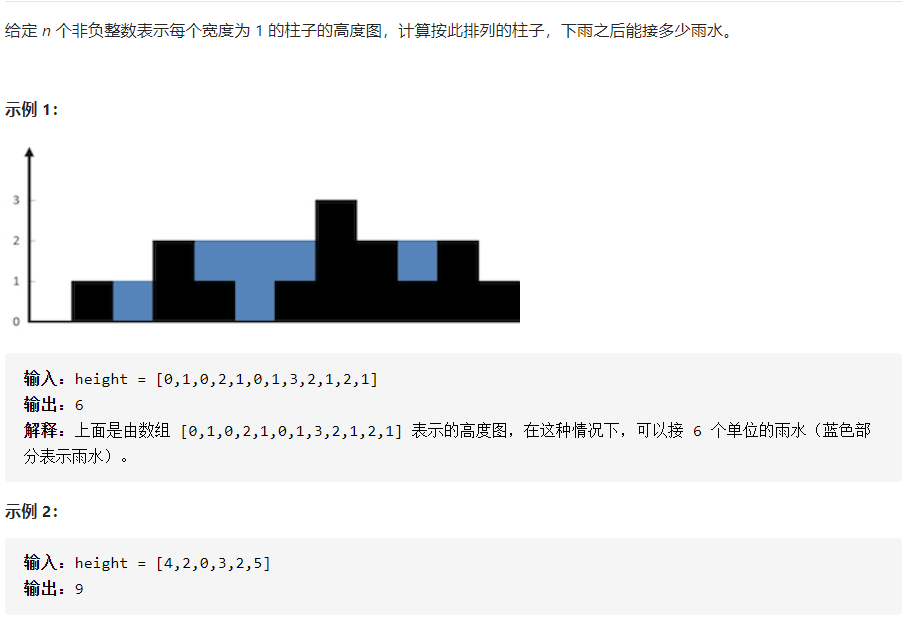
The area of the rectangle is roughly the same as that of the previous rectangle. This problem mainly finds two boundaries. The traversal element should be larger than the top element of the stack, and find the trough

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        int sum=0;
        for(int i=0;i<height.size();i++){
            while(!st.empty()&&height[i]>height[st.top()]){
                int right=height[i];
                int mid=st.top();
                st.pop();
                if(!st.empty()){
                    int h=min(height[st.top()],right)-height[mid];
                    int w=i-st.top()-1;
                    sum+=h*w;
                } 
            }
            st.push(i);
        }
        return sum;
    }
};