1. Delete all nodes in the linked list equal to the given value val
class Solution {
public ListNode removeElements(ListNode head, int val) {
if(head==null){
return null;
}
ListNode prev=head;
ListNode cur=head.next;
while(cur!=null){
if(cur.val==val){
cur=cur.next;
prev.next=cur;
}else{
prev=cur;
cur=cur.next;
}
}
if(head.val==val){
head=head.next;
}
return head;
}
}
2. Reverse a single linked list
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null || head.next==null){
return head;
}
ListNode cur=head;
ListNode newHead=null;
while(cur!=null){
ListNode curNext=cur.next;
cur.next=newHead;
newHead=cur;
cur=curNext;
}
return newHead;
}
}
Method: head inserting method (head inserting the first node from the second node)
be careful:
-
Inverse not only reverses the value, but reverses the node itself
-
If the inverted print result is incorrect by using the diplay method in the previous chapter, because the diplay method starts printing from the head node defined at the beginning, and now the real head node has changed, you can modify it
public void display2(Node newHead){ Node cur = newHead; while(cur!=null){ System.out.print(cur.val + " "); cur=cur.next; } System.out.println(); }
3. Given a non empty single linked list with head node, return the intermediate node of the linked list. If there are two intermediate nodes, the second intermediate node is returned
Method 1: find the number of nodes through traversal, and then find the intermediate node
class Solution {
public ListNode middleNode(ListNode head) {
if(head==null){
return null;
}
ListNode cur=head;
int count=0;
while(cur!=null){
count++;
cur=cur.next;
}
count=count/2+1;
ListNode node=head;
int i=0;
while(i!=count-1){
node=node.next;
i++;
}
return node;
}
}
Method 2: fast and slow pointer method (the fast pointer takes two steps at a time and the slow pointer takes one step at a time)
class Solution {
public ListNode middleNode(ListNode head) {
if(head==null){
return null;
}
ListNode fast=head;
ListNode slow=head;
while(fast!=null && fast.next!=null){
fast=fast.next.next;
slow=slow.next;
}
return slow;
}
}
4. Input a linked list and output the penultimate node in the linked list
Method 1: find the number of nodes through traversal, and then find the penultimate node
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
if(head==null){
return null;
}
ListNode cur = head;
int count=0;
while(cur!=null){
count++;
cur=cur.next;
}
if(k<1 || k>count){
return null;
}
ListNode node = head;
int i=0;
while(i!=count-k){
node=node.next;
i++;
}
return node;
}
}
Method 2: fast and slow pointer method (first let the fast pointer go k-1 steps, and then let the fast and slow pointers go at the same time)
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
if(head==null || k<=0){
return null;
}
ListNode fast=head;
ListNode slow=head;
while(k-1!=0){
fast=fast.next;
if(fast==null){
return null;
}
k--;
}
while(fast.next!=null){
fast=fast.next;
slow=slow.next;
}
return slow;
}
}
5. Merge the two ordered linked lists into a new ordered linked list and return. The new linked list is composed of all nodes of a given two linked lists
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1==null && l2==null){
return null;
}
if(l1==null && l2!=null){
return l2;
}
if(l2==null && l1!=null){
return l1;
}
ListNode node=new ListNode();
ListNode head=node;
while(l1!=null && l2!=null){
while(l1!=null && l2!=null && l1.val<=l2.val){
node.next=l1;
node=node.next;
l1=l1.next;
}
while(l1!=null && l2!=null && l1.val>l2.val){
node.next=l2;
node=node.next;
l2=l2.next;
}
}
if(l1!=null){
node.next=l1;
}
if(l2!=null){
node.next=l2;
}
return head.next;
}
}
6. Write code to divide the linked list into two parts based on the given value x, and all nodes less than X are arranged before nodes greater than or equal to X
public class Partition {
public ListNode partition(ListNode pHead, int x) {
if(pHead==null){
return null;
}
ListNode cur=pHead;
ListNode as=null;
ListNode ae=null;
ListNode bs=null;
ListNode be=null;
while(cur!=null){
if(cur.val<x){
if(bs==null){
bs=cur;
be=bs;
}else{
be.next=cur;
be=be.next;
}
}else{
if(as==null){
as=cur;
ae=as;
}else{
ae.next=cur;
ae=ae.next;
}
}
cur=cur.next;
}
if(bs==null){
return as;
}
be.next=as;
if(as!=null){
ae.next=null;
}
return bs;
}
}
Where bs, be, as and ae are the head and tail nodes at both ends less than X and greater than x respectively
7. There are duplicate nodes in a sorted linked list. Please delete the duplicate nodes in the linked list. The duplicate nodes are not retained and the chain header pointer is returned
public class Solution {
public ListNode deleteDuplication(ListNode pHead) {
if(pHead==null){
return null;
}
ListNode node=new ListNode(0);
ListNode newHead=node;
ListNode cur=pHead;
while(cur!=null){
if(cur.next!=null && cur.val==cur.next.val){
while(cur.next!=null && cur.val==cur.next.val){
cur=cur.next;
}
cur=cur.next;
}else{
newHead.next=cur;
newHead=newHead.next;
cur=cur.next;
}
}
newHead.next=null;
return node.next;
}
}
8. Palindrome structure of linked list
public class PalindromeList {
public boolean chkPalindrome(ListNode A) {
if(A==null){
return true;
}
if(A.next==null){
return true;
}
ListNode left=A;
ListNode mid=A;
ListNode right=A;
while(right!=null && right.next!=null){
right=right.next.next;
mid=mid.next;
}
ListNode cur=mid.next;
while(cur!=null){
ListNode curNext=cur.next;
cur.next=mid;
mid=cur;
cur=curNext;
}
while(mid!=left){
if(mid.val!=left.val){
return false;
}
if(left.next==mid){
return true;
}
mid=mid.next;
left=left.next;
}
return true;
}
}
method:
- Find intermediate node
- Reverse the linked list after the intermediate node
- Compare the head and tail of the inverted linked list
9. Enter two linked lists and find their first common node
public class Solution {
public int getLength(ListNode head){
if(head==null){
return 0;
}
int count=0;
while(head!=null){
count++;
head=head.next;
}
return count;
}
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null || headB==null){
return null;
}
ListNode cur1=headA;
ListNode cur2=headB;
int length1=getLength(headA);
int length2=getLength(headB);
int i=0;
if(length1>=length2){
while(i!=length1-length2){
cur1=cur1.next;
i++;
}
}else{
while(i!=length2-length1){
cur2=cur2.next;
i++;
}
}
while(cur1!=cur2){
cur1=cur1.next;
cur2=cur2.next;
}
return cur1;
}
}
Method: because after the common node, the nodes of the two linked lists are the same length. As long as the distance between the nodes moved by the two linked lists and the common node is equal before the common node, move step by step
10. Given a linked list, judge whether there are links in the linked list
public class Solution {
public boolean hasCycle(ListNode head) {
if(head==null){
return false;
}
if(head.next==null){
return false;
}
ListNode fast=head;
ListNode slow=head;
while(fast!=null && fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow){
return true;
}
}
return false;
}
}
Method: fast and slow pointer method (chase the slow pointer through the fast pointer, and if you can catch up, there is a ring)
11. Given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head==null || head.next==null){
return null;
}
ListNode fast=head;
ListNode slow=head;
while(fast!=null && fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow){
break;
}
}
if(fast==null || fast.next==null){
return null;
}
fast=head;
while(fast!=slow){
fast=fast.next;
slow=slow.next;
}
return fast;
}
}
Key: fast=head in the above question and the following code mean that after finding the public node, move step by step from the head node and intersection of the linked list. When the two nodes meet, it is the first public node
Analysis: the above key points can be analyzed and understood in combination with the following figure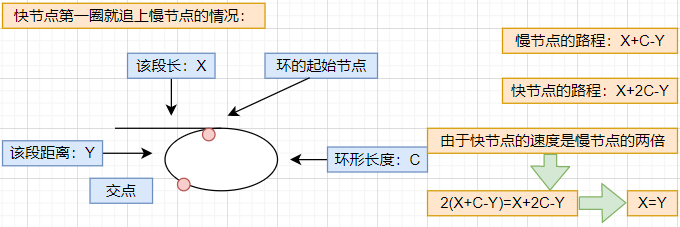
- When the first circle catches up: the conclusion is X=Y, so the two nodes can move one step at a time
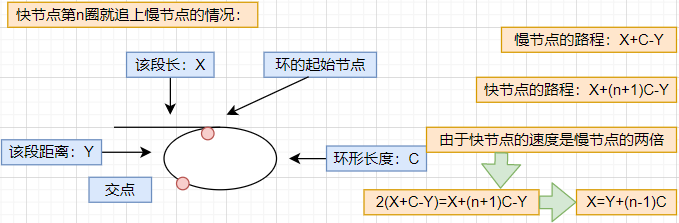
- When the nth circle catches up: the conclusion is X=Y+(n-1)C. Because the moving distance of the two nodes is the same, and after the node at the intersection moves n-1 circle, go Y just to the starting node. Therefore, the two nodes can move one step at a time
If you can easily deal with the above questions, you can continue to do them in the link below Leetcode OJ link and Niu Ke OJ link
Come on!