The abstract data type of linear table is defined in the sequential table storage structure and implemented by C + + class. Its template mechanism is as follows.

const int MaxSize = 100;
template <typename DataType>
class SeqList
{
public:
 SeqList( );                           //Create an empty sequence table
 SeqList(DataType a[ ], int n);        //Establish a sequence table with length n
 int Length( );                        //Constitutive function
 DataType Get(int i);                  //Find by bit to find the value of the ith element
 int Locate(DataType x );              //Find by value to find the element sequence number with value x
 void Insert(int i, DataType x);       //Insert operation, insert the element with the value of x at the ith position
 DtaType Delete(int i);                //Delete operation, delete the ith element
 int Empty( );                         //Judge whether the linear table is empty
 void PrintList( );                    //Traverse operation, and output each element in sequence according to sequence number
private:
 DataType data[MaxSize];               //An array of data elements
 int length;                           //Length of linear table
 //This code fragment comes from data structure -- from concept to C + + implementation -- Tsinghua University Press - 3rd Edition
};

Through this code fragment, we can have a preliminary understanding of the sequential table: member variables realize the storage structure of the sequential table, and member functions realize the basic operation of the linear table. For the SeqList library that has integrated sequential tables, this can make us almost bid farewell to the string library, and its member functions can complete the operations that are difficult for the basic functions in the string library. This is my personal first understanding of the practical value of linear tables.

The following describes the functions of member functions and their function definitions.

1. If there is no parameter constructor, you only need to initialize the sequence table, and only need to initialize the Length of the sequence table to 0. Its function prototype is as follows:

SeqList<DataType> :: SeqList( )
{
 Length = 0;
}

The function initializes the sequence table and creates an empty table.
This function prototype has neither input nor output. The most abstract way to understand it is that we can regard it as the initialization of an array. Although there are essential differences between array and sequential table, it is the purpose for us beginners to understand it with popular ideas as much as possible.

1. There is a parameter constructor, and a sequence table needs to be established
   To create a sequence table with a length of N, you need to pass the given n data elements into the sequence table to be established, and the number of elements passed in is the length of the sequence table. Let the given data element be stored in array a [n], and the constructor is defined as follows:

SeqList<DataType> :: SeqList(DataType a[ ], int n)
{
    if (n > MaxSize) throw "invalid parameter"; //If the number of data n is greater than the maximum storage space MaxSize of the sequence table, it cannot be established
    for (int i = 0; i < n; i++)
            data[i] = a[i];  //Transfer the data in a[n] into the linear table data []
    length = n;  //Given linear table Length = n
}

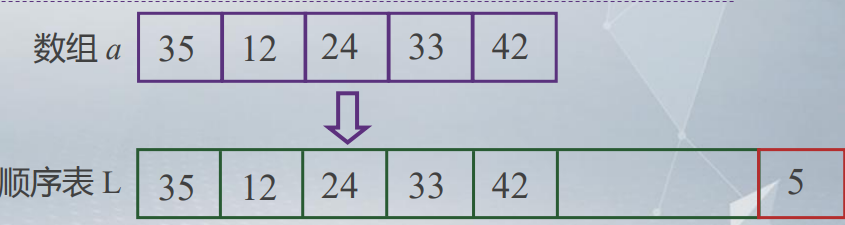
As shown in the figure, no matter how large the L space of the sequence table is, its Length only depends on the number of elements contained.
The 5 in the red box in this figure indicates that the length of this sequence table L is 5.
Therefore, when we need to determine whether a sequence table is an empty sequence table, we only need to determine whether the Length of the sequence table is 0.

1. How to find the length of the sequence table:
   In the class definition of the sequential table, the member variable length stores the length of the linear table. Therefore, to find the length of the linear table, only the value of the member variable length needs to be returned. The code is as follows:

int SeqList<DataType> :: Length( )
{
 return length ;
}

1. Sequential table member function -- bitwise search: DataType Get(int i)
   Function definition:

template <typename DataType>
DataType SeqList<DataType> :: Get(int i)
{
 if (i < 1 && i > length) throw "Illegal search location";
 else return data[i - 1];
}

Search by bit, just locate the memory location to be searched, and the time complexity bit is 0 (1)

1. Sequential table member function -- find by value: int Locate(DataType x)
   Function definition:

template <typename DataType>
int SeqList<DataType> :: Locate(DataType x)
{
 for (int i = 0; i < length; i++)
 if (data[i] == x) return i+1; //Returns its sequence number i+1
 return 0; //Exit the loop, indicating that the search failed
}

To find by value, you need to compare the value X to be found from the first memory until the value X to be found appears. It is assumed that the value appears at any position randomly, and the average time performance is 0(n)

1. Insertion function of sequential table: void Insert(int i, DataType x)
   Function definition:

template <typename DataType>
void SeqList<DataType> :: Insert(int i, DataType x)
{
 if (length == MaxSize) throw "Overflow";
 if (i < 1 || i > length + 1) throw "Insertion position error";
 for (int j = length; j >= i; j--)
 data[j] = data[j - 1]; //The j-th element exists at the subscript j-1 of the array
 data[i - 1] = x;
 length++;
}

It is easy to know by function definition:
When the table is full (length > = maxsize),
Re insertion will lead to memory overflow. At this time, the insertion operation will not be performed and "overflow" will be prompted.
Therefore, a reasonable insertion operation should meet the following conditions:
① Length <= MaxSize - 1
② 1 < = I < = length + 1 (I is the sequence number of the element, not the subscript of the element)

1. Deletion function of sequence table: DtaType Delete(int i);
   It is defined as follows:

template <typename DataType>
void SeqList<DataType> :: delete(int i)
{
    DataType x;
    if(length == 0) throw "Underflow" ;
    if(i < 1 || i > length) throw "Delete location error";
    x = data[i-1];  //Take out the element at position i
    for (int j = i; j < length; j++)
        data[j-1] = data[j];  //Here j is already the index of the array where the element is located
    length --;
    return x;
}

In the same way as insertion, memory can neither overflow nor underflow. Therefore, when the sequence table is empty, deletion cannot be performed at this time, and underflow will be prompted, and the location to be deleted must be legal, that is (1 < = I < = length).

This is the place for the preliminary understanding of the sequence table. The next time I update the actual use of the sequence table, I may find several practical examples from the Internet to analyze it. I will no longer use the old model program code in the teaching materials, but update it with luck.

If you think it's useful, remember to praise it. Bye.