2.5 application of queue - cardinality sorting

1. Algorithm Introduction

The key idea of cardinality sorting is "multi keyword sorting", which has two basic implementation methods

one ️⃣ Highest priority (MSD)

First arrange several subsequences according to the highest order, and then sort each subsequence according to the high order. Taking poker as an example, first arrange four subsequences according to the decor, then sort the 13 cards of each decor, and finally make the whole card orderly.

two ️⃣ Lowest priority (LSD)

This method does not need to be divided into subsequences first, and all keywords participate in each sorting. The lowest order can be carried out preferentially, not through comparison, but through "allocation" and "collection". Similarly, taking playing cards as an example, cards can be allocated to 13 buckets of 1 ~ 13 according to numbers, and then collected successively from the first bucket; Then distribute the collected cards to 4 buckets according to the design and color, which is also collected from the first bucket. After two "distribution" and "collection" operations, the cards are finally orderly

2. Algorithm flow

Take LSD as an example to illustrate the cardinality sorting process. The original sequence is 278 109 63 930 589 184 505 269 8 83

Each bit of each keyword is composed of numbers. The range of numbers is 0 ~ 9, so 10 buckets are prepared to put keywords. It should be noted that each bit of the keyword is not necessarily a number, but may also be the color of playing cards (4 buckets to be prepared), or English letters (26 buckets to be prepared if it is not size sensitive). The bucket here is a first in first out queue.

one ️⃣ Carry out the first assignment and collection according to the last digit

1) The allocation process is as follows (keywords enter from the top of the bucket)

The lowest point of 278 is 8. Put it into bucket 8

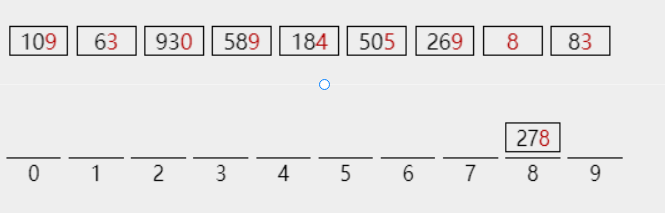
The lowest level of 109 is 9. Put it into bucket 9

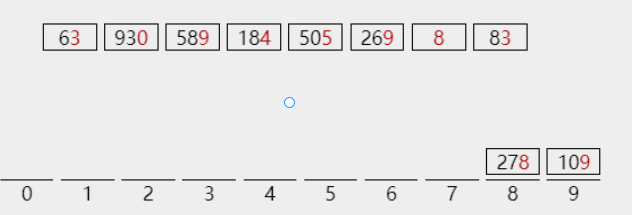
According to the above method, put the numbers into the bucket in turn to complete the first allocation

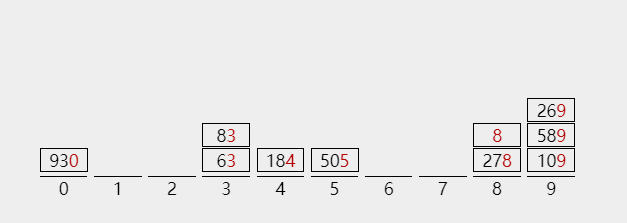
2) The collection process is as follows, in the order of 0 ~ 9. Note that keywords are collected from the bottom of the bucket

Barrel 0:930

Bucket 1: no collection

Bucket 2: no collection

Barrel 3: 63, 83

...

Barrel 8:278, 8

Barrel 9: 109589269

Arrange the keywords collected in order, and the result after the first collection is

930 63 83 184 505 278 8 109 589 269

two ️⃣ On the basis of the first sorting result, the second allocation and collection are carried out according to the middle position

1) The results of the second assignment are as follows

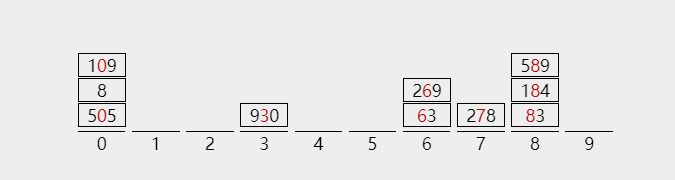
2) The collection process of the second trip is as follows:

Barrel 0:505, 8109

Bucket 1: no collection

Bucket 2: no collection

Barrel 3:930

...

Bucket 8:83184589

Bucket 9: no collection

The collection results of the second trip are as follows:

505 8 109 930 63 269 278 83 184 589

three ️⃣ On the basis of the sorting results of the second pass, allocate and collect the third pass according to the highest order

1) The allocation results of the third trip are as follows:

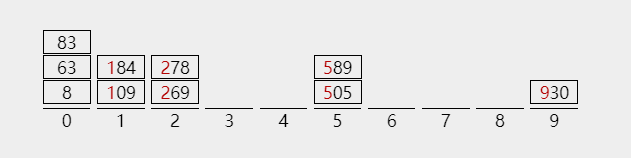
2) Carry out the third collection

Barrel 0:8, 63, 83

Barrel 1:109184

Barrel 2: 269178

Bucket 3: no collection

...

Bucket 8: no collection

Barrel 9:930

The collection results of the third trip are as follows:

8 63 83 109 184 269 278 505 589 930

At this time, the highest bit is ordered, the keywords with the same highest bit are ordered according to the middle bit, and the keywords with the same middle bit are ordered according to the lowest bit, so the whole sequence is ordered and the cardinality sorting ends

The cardinality sorting of LSD is applicable to the sequence with small digits. If there are many digits, the efficiency of using MSD will be better. In contrast to LSD, MSD is allocated based on the high-order number, but it is not merged back into an array immediately after allocation. Instead, a "sub bucket" is established in each "bucket", and the value in each bucket is allocated to the "sub bucket" according to the value of the next digit. After the allocation of the lowest digits is completed, it is merged into the array of receipt 1.

3. Algorithm performance analysis

Time complexity: average and worst case O ( d ( n + r d ) ) O(d(n+r_{d})) O(d(n+rd​))

Space complexity: O ( r d ) O(r_{d}) O(rd​)

Where, n is the number of key words in the sequence, D is the number of key words of the keyword, such as 930, which is composed of 3 bits, d=3; r d r_{d} rd ＾ is the number of keyword bases. The base here refers to the symbols constituting the keyword. For example, when the keyword is a numerical value, the symbols constituting the keyword are 0 ~ 9, a total of ten, so r d = 10 r_{d}=10 rd​=10

⭐ Key words: time complexity analysis

The cardinality sort is allocated and collected for each trip. Each keyword in the sequence needs to be allocated in sequence, that is, the whole sequence needs to be scanned in sequence, so there is n; Each bucket needs to be collected in turn, and the number of buckets depends on the value range of keywords. For example, there are 10 buckets for numbers and 26 buckets for letters r d r_{d} rd, so there are r d r_{d} rd ， this item, so it takes time to allocate and collect n + r d n+r_{d} n+rd​ . The number of times required for the whole sorting is the number of keywords, i.e. d. Therefore, the time complexity of cardinality sorting is O ( d ( n + r d ) ) O(d(n+r_{d})) O(d(n+rd​))

4. Examples

The queue is used to sort a data sequence (cardinality sorting). The data of the data sequence (described in Articles 1 and 2) and the storage mode of the queue (described in Article 3) have the following requirements:

1) When the data sequence is integer data, the number of bits of each data in the data sequence does not require equal width, such as 1, 21, 12, 322, 44, 123, 2312, 765 and 56

2) When the data sequence is string type data, each string in the data sequence is of equal width, such as "abc", "bde", "fad", "abd", "bef", "fdd", "abe"

3) It is required to rebuild the storage representation of queues: enable it to map n queues into an array listArray in order, and each queue is represented as a circular queue in memory [this item is optional]

Idea: for numbers and equal length strings, the lowest order priority method can be used; For requirement 3, that is to use a storage array to store the values of multiple queues. At this time, you can use the pointer arrays front[n] and rear[n] to solve it, and pay attention to the change of the array subscript (I refer to the boss's answer for this question, so I won't release it)

public class RadixSort {
    public static void LSD(int[] num) {
        //The numbers are sorted by the lowest priority method
        MyQueue queue = new MyQueue(10, num.length);//Allocate 10 queues
        int digits = getNumDigits(num);
        int mode = 1;
        while (digits != 0) {
            for (int i = 0; i < num.length; i++) {
                queue.enqueue((num[i] / mode) % 10, num[i]);
                //Allocate by bucket, (num[i]/mode)%10 indicates the number of bits taken
            }
            int k = 0;
            for (int j = 0; j < 10; j++) {
                while (!queue.isEmpty(j)) {
                    num[k] = (int) queue.dequeue(j);
                    k++;
                }
            }//Out of the team
            digits--;//Bit up
            mode = mode * 10;
        }
    }

    public static void LSD(String[] str) {
        //Take the lowest priority method for strings
        //The numbers are sorted by the lowest priority method
        MyQueue queue = new MyQueue(27, str.length);//Assign 27 queues
        //27 buckets, of which the 27th bucket is used to store characters other than letters, and is not case sensitive
        int digits = str[0].length();//Length of equal length characters
        int mode = 1;
        while (digits != 0) {
            for (int i = 0; i < str.length; i++) {
                int index;//Subscript of bucket
                if (str[i].charAt(digits - 1) >= 'A' && str[i].charAt(digits - 1) <= 'Z') {
                    index = str[i].charAt(digits - 1) - 'A';
                } else if (str[i].charAt(digits - 1) >= 'a' && str[i].charAt(digits - 1) <= 'z') {
                    index = str[i].charAt(digits - 1) - 'a';
                } else {
                    index = 26;
                }//Case insensitive
                queue.enqueue(index, str[i]);
                //Distribution by bucket
            }
            int k = 0;
            for (int j = 0; j < 27; j++) {
                while (!queue.isEmpty(j)) {
                    str[k] = (String) queue.dequeue(j);
                    k++;
                }
            }//Out of the team
            digits--;//Bit up
        }
    }

    static int getNumDigits(int[] num) {//Get the number of digits of the maximum number
        int max = num[0];//Maximum number
        int digits = 0;//digit
        for (int i = 0; i < num.length; i++) {
            if (num[i] > max) max = num[i];
        }
        while (max / 10 != 0) {
            digits++;
            max = max / 10;
        }
        if (max % 10 != 0) {
            digits++;
        }
        return digits;
    }


    public static void main(String[] args) {
        int[] num = {12, 32, 2, 231, 14, 23};
        System.out.println("before sorting: " + Arrays.toString(num));
        LSD(num);
        System.out.println("after sorting: " + Arrays.toString(num));
        String[] strings = {"abc", "bde", "fad", "abd", "bef", "fdd ", "abe" };
        System.out.println("before sorting: " + Arrays.toString(strings));
        LSD(strings);
        System.out.println("after sorting: " + Arrays.toString(strings));
    }
}

The operation results are as follows

before sorting: [12, 32, 2, 231, 14, 23]
after sorting: [2, 12, 14, 23, 32, 231]
before sorting: [abc, bde, fad, abd, bef, fdd , abe]
after sorting: [abc, abd, abe, bde, bef, fad, fdd ]