Introduction: today, I was laughed by this question and woke up by this question. It turns out that I haven't really understood KMP algorithm
Let's talk about how interesting this problem is:
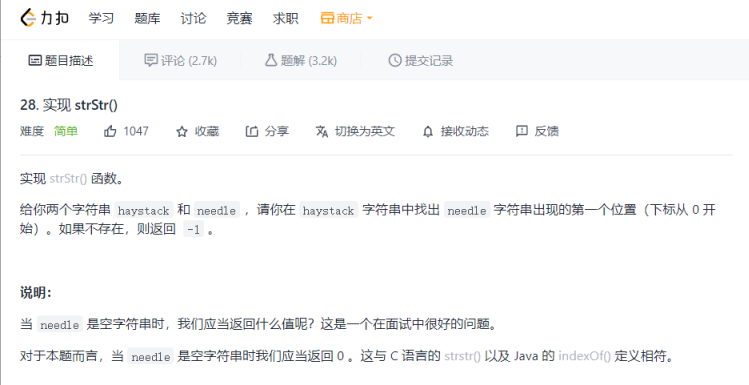
I:
For those who are familiar with object-oriented encapsulation, only one line of code is needed to solve this problem. Hahaha, I was laughed at. The following is Java code:
return haystack.indexOf(needle);
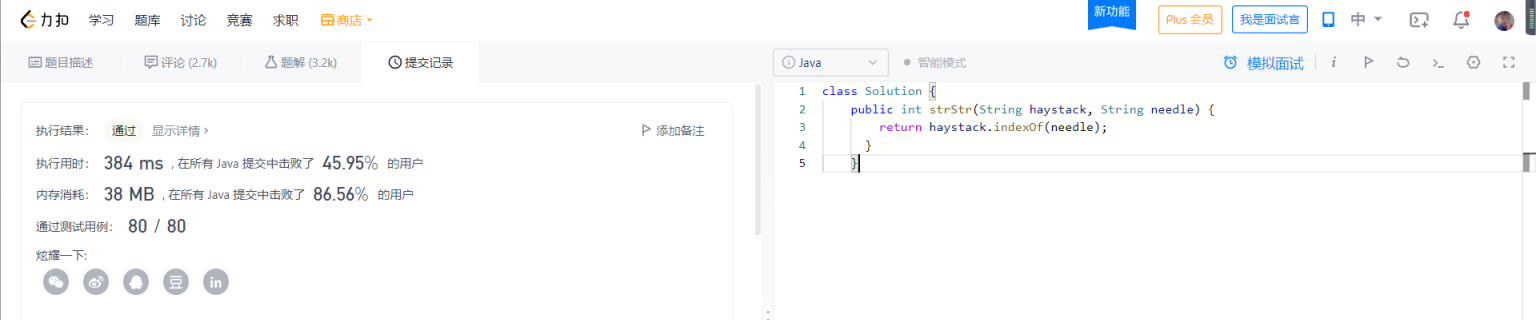
OK, this is the end of today's interview. You can go back and wait for the notice
II
Violence enumeration: each is compared
class Solution {
public int strStr(String haystack, String needle) {
if(needle.equals("")) return 0;
int slow, fast, m = haystack.length(), n = needle.length(), k;
for(slow = 0; slow < m - n + 1; slow++){
k = slow;
for(fast = 0; fast < n; fast++){
if(haystack.charAt(k) != needle.charAt(fast))
break;
k++;
}
if(fast == n) return slow;
}
return -1;
}
}
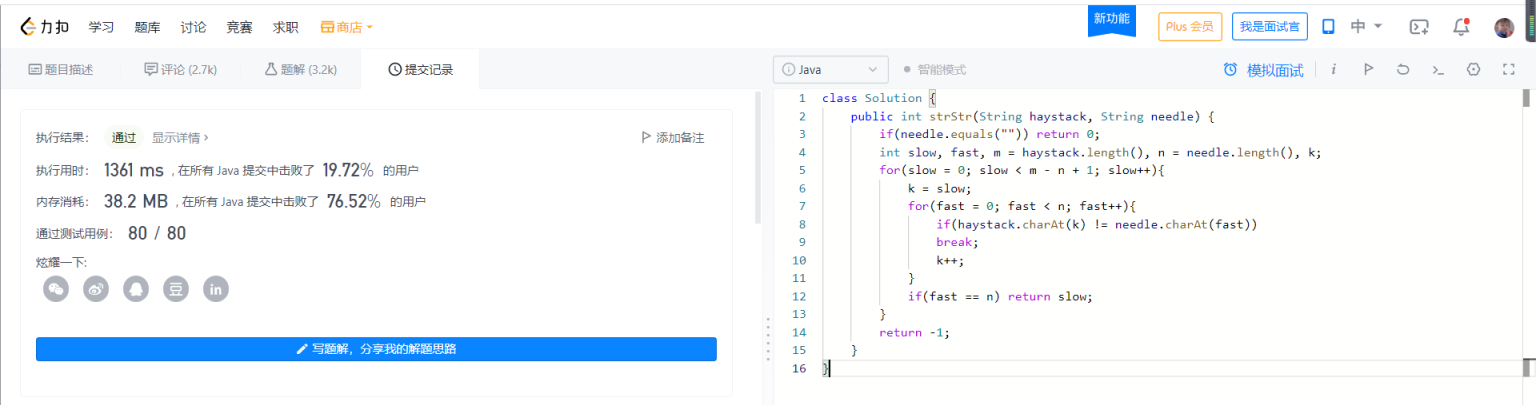
Although everything is OK, the performance is too poor, so the following protagonists appear ----------- KMP algorithm, which specializes in various substring matching:
I'm ashamed to say that I forgot how to calculate before using it, so I went to look through the data again. Stimulated by the desire to win or lose, I wanted to complete the KMP algorithm completely, steadfastly and deeply, take notes and understand every detail
Let's introduce two concepts first: getNext array is used
Prefix: contains the first character and does not contain the last character
Suffix: contains the last character and does not contain the first character
Note: the comparison between prefix string and suffix string is from left to right!!
Statement: you can follow and practice more by yourself, which is very helpful to understand the subsequent code
1. First, get the next [] array. Let's go directly to the figure above and deduct the word description fee

If necessary, just write a few more examples. Handwriting is not difficult, mainly because the code is hard to understand
Then go directly to the code:
public static void getNext(int[] next, String sonStr){
int len = sonStr.length();
char[] ch = sonStr.toCharArray();
int i = 0, k = 1;/*Find the number of characters with the same prefix and suffix from the third,
//i Indicates the beginning of the prefix, and k indicates the beginning of the suffix (i.e. j-1 each time)
Therefore, the expression of j is: k+1 */
next[0] = -1;
next[1] = 0;
while(k < len - 1 ){
if(i != -1 && ch[i] == ch[k]){
next[k+1] = i + 1;/*
Here is the assignment of j,
Since i starts from 0, the number of calculations should be + 1
*/
i++;
k++;
}
else if(i == -1){
next[k + 1] = 0;
/*If i == -1, it means that there is no same character before the suffix of the j, assign a value of 0, and then continue to compare the next one, so k++
Then the prefix continues to start with the first, that is, the subscript 0, so i++
*/
i++;
k++;
}
else{
//Here is the key point. i = next[i], I personally think it is suspected of dynamic programming
//Because the Prefix suffix here does not match, but maybe the prefix i can match the suffix by reversing a few spaces
//Therefore, we need to know where our i will be pushed back with the help of the previous value. Returning to - 1 means that it does not match, so it is suspected of dynamic programming
i = next[i];
}
}
}
Let's start the analysis: (the code has comments, you can see)
1: The next array has two special values: next[0] = -1, and next[1] = 0. You can directly assign a value to next [] each time. Because there is only one character before next[1], it contains the first character and the last character, so it can not be compared (according to the definition of prefix and suffix).
Therefore, it also shows that the method can be called only when the substring exceeds 2 characters, otherwise an error will be reported
II:
This method seeks the j-th, but it starts from the J-1, and J-1 depends on the result of J-2, so it is suspected of dynamic programming,
See the explanation of the above code for details
Finally, attach the complete debugging code:
package FirstPackage;
public class KMP {
public static void main(String[] args) {
String fatherStr = "mississippi";
String sonStr = "issip";
System.out.println(testKMP(fatherStr,sonStr));
}
public static int testKMP(String fatherStr,String sonStr) {
int n = fatherStr.length(), m = sonStr.length();
if(m == 0) return 0;
else if(m < 2) {
return fatherStr.indexOf(sonStr.charAt(0));
}
else {
int[] next = new int[m];
getNext(next, sonStr);
int i = 0, j = 0;
//The while loop must be written in this way. Neither of them can be established, otherwise the subscript will cross the boundary
while( j < n && i < m ) {
if(i == -1 || fatherStr.charAt(j) == sonStr.charAt(i)) {
i++;
j++;
}
else i = next[i]; //If i don't match, i will go back where i should go
}
if(i == m) return j - i; //For example, by hand, this is the value
else return -1;
}
}
public static void getNext(int[] next, String sonStr){
int len = sonStr.length();
char[] ch = sonStr.toCharArray();
int i = 0, k = 1;
next[0] = -1;
next[1] = 0;
while(k < len - 1 ){
if(i != -1 && ch[i] == ch[k]){
next[k+1] = i + 1;
i++;
k++;
}
else if(i == -1){
next[k + 1] = 0;
i++;
k++;
}
else{
i = next[i];
}
}
}
}
Then we submit the results to see the performance of KMP:
The test code is as follows: – all possible situations are considered here
class Solution {
public int strStr(String haystack, String needle) {
int n = haystack.length(), m = needle.length();
if(m == 0) return 0;
else if(m < 2) {
return haystack.indexOf(needle.charAt(0));
}
else {
int[] next = new int[m];
getNext(next, needle);
int i = 0, j = 0;
while( j < n && i < m ) {
if(i == -1 || haystack.charAt(j) == needle.charAt(i)) {
i++;
j++;
}
else i = next[i];
}
if(i == m) return j - i;
else return -1;
}
}
public static void getNext(int[] next, String sonStr){
int len = sonStr.length();
char[] ch = sonStr.toCharArray();
int i = 0, k = 1;
next[0] = -1;
next[1] = 0;
while(k < len - 1 ){
if(i != -1 && ch[i] == ch[k]){
next[k+1] = i + 1;
i++;
k++;
}
else if(i == -1){
next[k + 1] = 0;
i++;
k++;
}
else{
i = next[i];
}
}
}
}
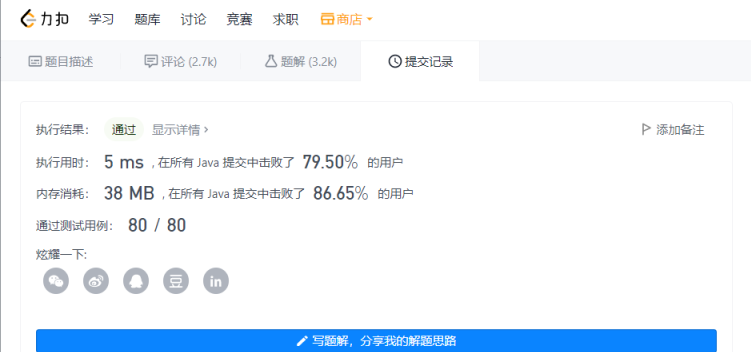
Wow giao, the algorithms that big guys study are different. For me, a rookie, just stand on the shoulders of giants, remember and learn their thoughts
Well, this article is finally over. I hope I can really understand the thoughts of the giants this time, and I won't turn over the information again and again