3.2 travel and implementation of binary tree

3.2.1 travel around binary tree

Visiting the nodes of a binary tree in a certain order is called a tour or traversal. Each node is accessed once and listed, which is called the enumeration of binary tree. Generally, the traversal of a binary tree is divided into pre order traversal, middle order traversal and post order traversal. The following figure illustrates the binary tree.

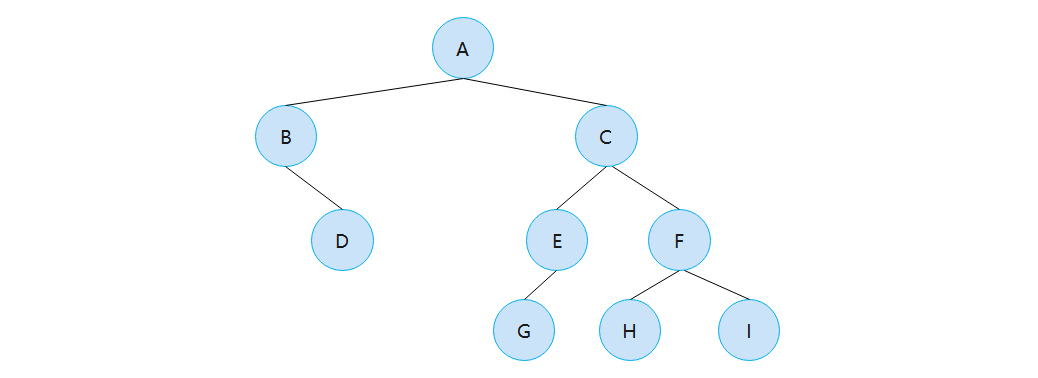
Pre order Tour: visit the node first, and then its child nodes. The results of the previous tour in the figure above are a, B, D, C, e, G, h and I

Second order Tour: first visit the child nodes (including their subtrees) of the node, and then visit the node. The binary tree in the figure above is enumerated after a sequential tour. The results are: D,B,G,E,H,I,F,C,A

Middle order Tour: first access the left child node (including the whole subtree), then the node, and finally access the right child node (including the whole subtree). The binary tree in the figure above is enumerated after a sequential tour, and the results are: B,D,A,G,E,C,H,F,I

The traveling route can be easily realized by recursion. The root node pointer is passed in the initial call, and then the nodes and their children are traveled in a given order. Take the previous tour as an example:

 void preOrder(BinNode root){
 	if(root==null) return;//Empty tree
 	visit(root);
 	preOrder(root.getLeft());
 	preOrder(root.getRight());
 }

For middle order tour and post order tour, you only need to modify the order of the last three methods.

3.2.2 implementation of binary tree

There are two ways to realize binary tree, sequential storage, that is, array storage, chain storage and pointer storage.

Analysis of array storage mode

Advantages: it is fast to access elements by subscript. For ordered arrays, binary search can also be used to improve the retrieval speed.

Disadvantages: if a specific value is to be retrieved, or the inserted value (in a certain order) will move as a whole, which is inefficient

Analysis of chain storage mode

Advantages: the array storage method is optimized to a certain extent (for example, if you insert a numeric node, you only need to link the inserted node to the linked list, and the deletion efficiency is also very good).

Disadvantages: when retrieving, the efficiency is still low, for example (to retrieve a value, you need to traverse from the beginning of the node)

1. Implementation of chain binary tree

For the chain storage structure, we need to define a chain node structure with one data field and two pointer fields, where left is the left child node, element is the data element and right is the right child node. Node definition and binary tree representation are as follows:

For chain node, it is defined as follows:

public class BinNodePtr {
    //Node class of chained binary tree
    private Object element;//Elements that store data
    private BinNodePtr left;//Left child node
    private BinNodePtr right;//Right child node

    //constructor section
    public BinNodePtr(){}
    public BinNodePtr(Object element){
        this.element=element;
    }

    //getter and setter parts
    public Object getElement() {
        return element;
    }

    public void setElement(Object element) {
        this.element = element;
    }

    public BinNodePtr getLeft() {
        return left;
    }

    public void setLeft(BinNodePtr left) {
        this.left = left;
    }

    public BinNodePtr getRight() {
        return right;
    }

    public void setRight(BinNodePtr right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "BinNodePtr{" +
                "element=" + element +
                '}';
    }
}

In the chain binary tree, there is only one private attribute root, which represents the root node of the tree. For a simple binary tree, we only define its traversal method, search method and deletion method.

For its traversal method, I have used three methods, which have been explained when I introduced traveling earlier

    //Preorder traversal
    public void preOrder(BinNodePtr node) {
        if (node != null) {
            System.out.println(node);
            preOrder(node.getLeft());
            preOrder(node.getRight());
        } else return;
    }

    //Medium order traversal
    public void infixOrder(BinNodePtr node) {
        if (node != null) {
            preOrder(node.getLeft());
            System.out.println(node);
            preOrder(node.getRight());
        } else return;
    }

    //Postorder traversal
    public void postOrder(BinNodePtr node) {
        if (node != null) {
            preOrder(node.getLeft());
            preOrder(node.getRight());
            System.out.println(node);
        } else return;
    }

Then search. You can also use pre order, middle order and post order:

    /*
     * @Description: Use the preceding sequence, the middle sequence and the following sequence to find the element respectively
     * @Author yjq
     * @Date 2021/9/21 21:05
     * @Param node, element
     * @Return If the node is found, null will be returned
     * @Exception
     */
    //Preorder search
    public BinNodePtr preOrderSearch(BinNodePtr node, Object element) {
        if (node != null) {
            if (node.getElement().equals(element)) {
                return node;//Compare the current node first
            }
            BinNodePtr temp = null;
            if (node.getLeft() != null) {
                temp = preOrderSearch(node.getLeft(), element);
                //If the left child node is not empty, the preceding recursive search is followed
            }
            if (temp != null) {
                return temp;//The return value is not null. Description found
            }
            if (node.getRight() != null) {
                temp = preOrderSearch(node.getRight(), element);
            }
            return temp;
        } else {
            return null;
        }
    }

    //Middle order search
    public BinNodePtr infixOrderSearch(BinNodePtr node, Object element) {
        if (node != null) {
            BinNodePtr temp = null;
            if (node.getLeft() != null) {
                temp = infixOrderSearch(node.getLeft(), element);
                //If the left child node is not empty, the preceding recursive search is followed
            }
            if (temp != null) {
                return temp;//The return value is not null. Description found
            }
            if (node.getElement().equals(element)) {
                return node;//Compare current node
            }
            if (node.getRight() != null) {
                temp = infixOrderSearch(node.getRight(), element);
            }
            return temp;
        } else {
            return null;
        }
    }

    //Sequential search
    public BinNodePtr postOrderSearch(BinNodePtr node, Object element) {
        if (node != null) {
            BinNodePtr temp = null;
            if (node.getLeft() != null) {
                temp = postOrderSearch(node.getLeft(), element);
                //If the left child node is not empty, the preceding recursive search is followed
            }
            if (temp != null) {
                return temp;//The return value is not null. Description found
            }
            if (node.getRight() != null) {
                temp = postOrderSearch(node.getRight(), element);
            }
            if (temp != null) {
                return temp;//The return value is not null. Description found
            }
            if (node.getElement().equals(element)) {
                return node;//Compare current node
            }
            return temp;
        } else {
            return null;
        }
    }

Finally, delete the node. It will be more difficult here. Note that we want to compare the child nodes of the current node, not the current node.

    /*
     * Recursively delete nodes
     * There are two cases: if a leaf node is deleted, delete the node 4
     * If a non leaf node is deleted, the subtree is deleted
     */
    public void delNode(BinNodePtr node, Object element) {
        //It should be noted that we judge whether the child nodes of the current node need to be deleted,
        //Instead of judging whether the current node needs to be deleted
        if (node.equals(root)&&node==null){
            System.out.println("the tree is empty!");
        }
        if (node.getLeft() != null) {
            if (node.getLeft().getElement().equals(element)){
                node.setLeft(null);
                return;
            }else {
                delNode(node.getLeft(),element);//Recursive deletion of left subtree
            }
        }
        if (node.getRight()!=null){
            if (node.getRight().getElement().equals(element)){
                node.setRight(null);
                return;
            }else {
                delNode(node.getRight(),element);//Recursive deletion of right subtree
            }
        }
    }

Finally, test:

public class BinaryTreePtrTest {
    public static void main(String[] args) {
        BinaryTreePtr test = new BinaryTreePtr();
        //Create node
        BinNodePtr root = new BinNodePtr("A");
        BinNodePtr node1 = new BinNodePtr("B");
        BinNodePtr node2 = new BinNodePtr("C");
        BinNodePtr node3 = new BinNodePtr("D");
        BinNodePtr node4 = new BinNodePtr("E");
        BinNodePtr node5 = new BinNodePtr("F");
        BinNodePtr node6 = new BinNodePtr("G");
        BinNodePtr node7 = new BinNodePtr("H");
        BinNodePtr node8 = new BinNodePtr("I");

        //Temporarily create a binary tree manually
        test.setRoot(root);
        root.setLeft(node1);
        root.setRight(node2);
        node1.setRight(node3);
        node2.setLeft(node4);
        node2.setRight(node5);
        node4.setLeft(node6);
        node5.setLeft(node7);
        node5.setRight(node8);

        //Traversal test
        System.out.println("Preface Tour");
        test.preOrder(test.getRoot());
        System.out.println("Middle order Tour");
        test.infixOrder(test.getRoot());
        System.out.println("Post order Tour");
        test.postOrder(test.getRoot());

        //Find test
        System.out.println("lookup B");
        System.out.println(test.infixOrderSearch(test.getRoot(),"B"));

        //Delete test
        System.out.println("delete C");
        test.delNode(test.getRoot(),"C");
        test.infixOrder(test.getRoot());
    }
}

The test results are as follows:

Preface Tour
BinNodePtr{element=A}
BinNodePtr{element=B}
BinNodePtr{element=D}
BinNodePtr{element=C}
BinNodePtr{element=E}
BinNodePtr{element=G}
BinNodePtr{element=F}
BinNodePtr{element=H}
BinNodePtr{element=I}
Middle order Tour
BinNodePtr{element=B}
BinNodePtr{element=D}
BinNodePtr{element=A}
BinNodePtr{element=C}
BinNodePtr{element=E}
BinNodePtr{element=G}
BinNodePtr{element=F}
BinNodePtr{element=H}
BinNodePtr{element=I}
Post order Tour
BinNodePtr{element=B}
BinNodePtr{element=D}
BinNodePtr{element=C}
BinNodePtr{element=E}
BinNodePtr{element=G}
BinNodePtr{element=F}
BinNodePtr{element=H}
BinNodePtr{element=I}
BinNodePtr{element=A}
lookup B
BinNodePtr{element=B}
delete C
BinNodePtr{element=B}
BinNodePtr{element=D}
BinNodePtr{element=A}

Process finished with exit code 0

2. Sequential binary tree

Sequential binary trees are generally complete binary trees, which will be used in subsequent heap sorting, and will be explained in detail at that time. The sequential binary tree is realized by array, and the binary tree with n nodes can be realized by array with size n, so there is no structural overhead, which is better than chain storage. Moreover, there is a rule between the subscripts of each node's parent node and child node as follows:

In the formula, r represents the subscript of the node, and n represents the total number of binary tree nodes:

1️⃣ P a r e n t ( r ) = ( r − 1 ) / 2 0 < r < n Parent(r)=(r-1)/2 \qquad 0<r<n Parent(r)=(r−1)/20<r<n

2️⃣ L e f t c h i l d ( r ) = 2 r + 1 2 r + 1 < n Leftchild(r)=2r+1 \qquad2r+1<n Leftchild(r)=2r+12r+1<n

3️⃣ R i g h t c h i l d ( r ) = 2 r + 2 2 r + 2 < n Rightchild(r)=2r+2\qquad2r+2<n Rightchild(r)=2r+22r+2<n

4️⃣ L e f t s i b l i n g ( r ) = r − 1 When r by even number and And 0 < r < n Time Leftsibling(r)=r-1\qquad when r is even and 0 < r < n Leftsibling(r)=r − 1 when r is even and 0 < r < n

5️⃣ R i g h t s i b l i n g ( r ) = r + 1 When r by odd number and And r + 1 < n Time Rightsibling(r)=r+1\qquad when r is odd and r + 1 < n Rightsibling(r)=r+1 when r is odd and r + 1 < n