Punch in day13

Question 1: Sword finger Offer 55 - I. depth of binary tree

Enter the root node of a binary tree to find the depth of the tree. The nodes (including root and leaf nodes) passing from root node to leaf node form a path of the tree, and the length of the longest path is the depth of the tree.

For example:

Given binary tree [3,9,20,null,null,15,7],

  3
 / \
 9  20
   /  \
  15   7

Returns its maximum depth 3.

**Prompt: * * total number of nodes < = 10000

Source: LeetCode
Link: https://leetcode-cn.com/problems/er-cha-shu-de-shen-du-lcof

Problem solving ideas:
The postorder traversal of the tree (depth first search) is often implemented by recursion or stack
Key point: the relationship between the depth of the tree and the depth of its left (right) subtree.
The depth of the tree is equal to the maximum of the depth of the left subtree and the depth of the right subtree + 1.

java code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        //Special case, when root is empty
        if(root == null){
            return 0;
        }
        int left = maxDepth(root.left);//Depth of left subtree 
        int right = maxDepth(root.right);//Depth of right subtree 
        return Math.max(left, right)+1;
    }
}

Question 2: Sword finger Offer 55 - II. Balanced binary tree

Enter the root node of a binary tree to judge whether the tree is a balanced binary tree. If the depth difference between the left and right subtrees of any node in a binary tree is no more than 1, it is a balanced binary tree.

Example 1:
Given binary tree [3,9,20,null,null,15,7]

  3
 / \
 9  20
    /  \
   15   7

Returns true.

Example 2:
Given binary tree [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

Returns false.

Limitations:
0 < = number of nodes in the tree < = 10000

Source: LeetCode
Link: https://leetcode-cn.com/problems/ping-heng-er-cha-shu-lcof

Problem solving ideas:
As in the above question, the depth of the tree is equal to the maximum of the depth of the left subtree and the depth of the right subtree + 1.
You can construct a function depth(root) to obtain the depth of the current subtree (that is, the previous question), and judge whether a subtree is a binary balanced tree by comparing the depth difference ABS (depth (root. Left) - depth (root. Right)) < = 1 between the left and right subtrees of a subtree. If all subtrees are balanced, the tree is balanced.

java code:

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    private int depth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(depth(root.left), depth(root.right)) + 1;
    }
}

Question 3: Sword finger Offer 68 - I. nearest common ancestor of binary search tree

Given a binary search tree, find the nearest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."

For example, give the following binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

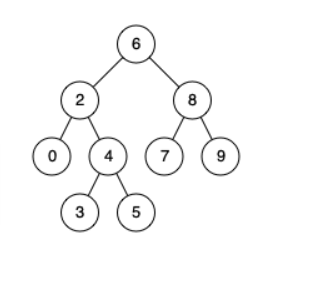
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: the nearest common ancestor of node 2 and node 8 is 6.

Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: the nearest common ancestor of node 2 and node 4 is 2, because according to the definition, the nearest common ancestor node can be the node itself.

explain:
The values of all nodes are unique.
p. q is different nodes and exists in a given binary search tree.

Source: LeetCode
Link: https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof

Problem solving ideas:
Definition of ancestor: if node pp is in the left (right) subtree of node root, or p = root, root is said to be the ancestor of p
This problem gives two important conditions: ① the tree is a binary search tree, and ② the values of all nodes of the tree are unique. According to the above conditions, it is convenient to judge the subtree relationship between p,q and root, that is:

If root.val < p.val, pp is in the right subtree of root;
If root.val > p.val, pp is in the left subtree of root;
If root.val = p.val, pp and root point to the same node.

java code:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while(root != null) {
            if(root.val < p.val && root.val < q.val) // p. Q is in the right subtree of root
                root = root.right; // Traverse to the right child node
            else if(root.val > p.val && root.val > q.val) // p. Q is in the left subtree of root
                root = root.left; // Traverse to left child node
            else break;
        }
        return root;
    }
}