Reminder:
1. The pictures taken in this article are from books:
Algorithm book for everyone [Japan] written by Shanpu Xian; Jueyun translation
2. The default sorting algorithm in this paper is ascending

Sorting algorithm summary: 1. Bucket sorting 2. Selection sorting 3. Bubble sorting 4. Insertion sorting 5. Merge sorting 6. Hill sorting 7. Quick sorting

1. Bucket sorting

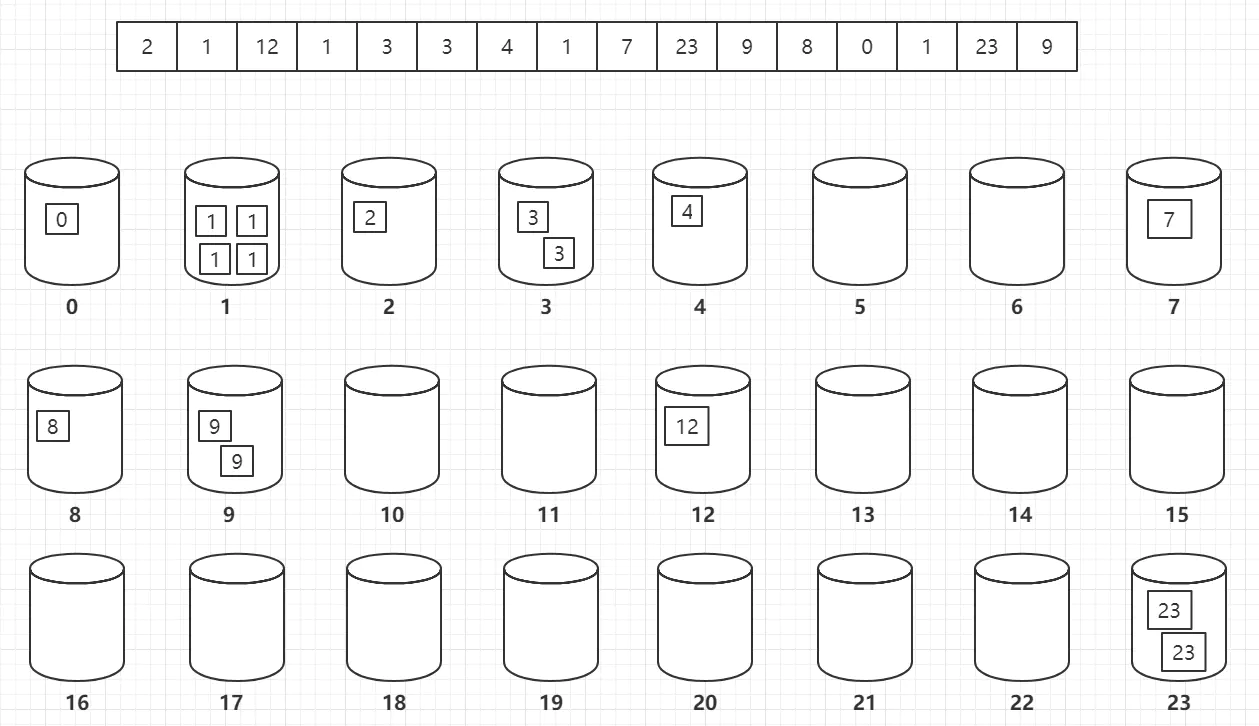
Traverse each element in the bucket in order and put it into the array in order to complete the sorting of the array.

A "bucket" is a container that can be implemented with a variety of data structures, including arrays, queues, or stacks.

(the following question was originally a leetcode question, but here is only for practicing simple bucket sorting. The conditional integer array nums – > positive integer array nums is changed)

front K High frequency element
 Here you are*Positive integer array nums* And an integer k ，Please return to the frequency before k High element. You can return answers in any order.
Example 1:

input: nums = [1,1,1,2,2,3], k = 2
 output: [1,2]
Example 2:

input: nums = [1], k = 1
 output: [1]
 

Tips:

1 <= nums.length <= 10^5
k The value range of is [1, The number of different elements in the array]
The question data ensures that the answer is unique, in other words, the first one in the array k The set of high frequency elements is unique

Bucket sorting solution
Python

 bucketN=max(nums)+1 #Prepare the maximum value in nums plus a bucket
 buckets=[0]*bucketN #The frequency of initializing all buckets is 0

 for i in nums:
     buckets[i]+=1 #Each number in nums corresponds to the serial number of the bucket. The value in the bucket records the frequency of this number
 
 result=sorted(enumerate(buckets),key=lambda X:X[1],reverse=True) #Sort according to lambda X:X[1], that is, sort according to the value in the bucket (the number appears in nums), and sort from small to large
 ans=[]
 for j in range(k):
     ans.append(result[j][0]) #Output the first K high frequency elements
 return ans

2. Select Sorting

Basic idea: select the smallest (or largest) element from the data elements to be sorted in each trip as the first element until all elements are arranged.

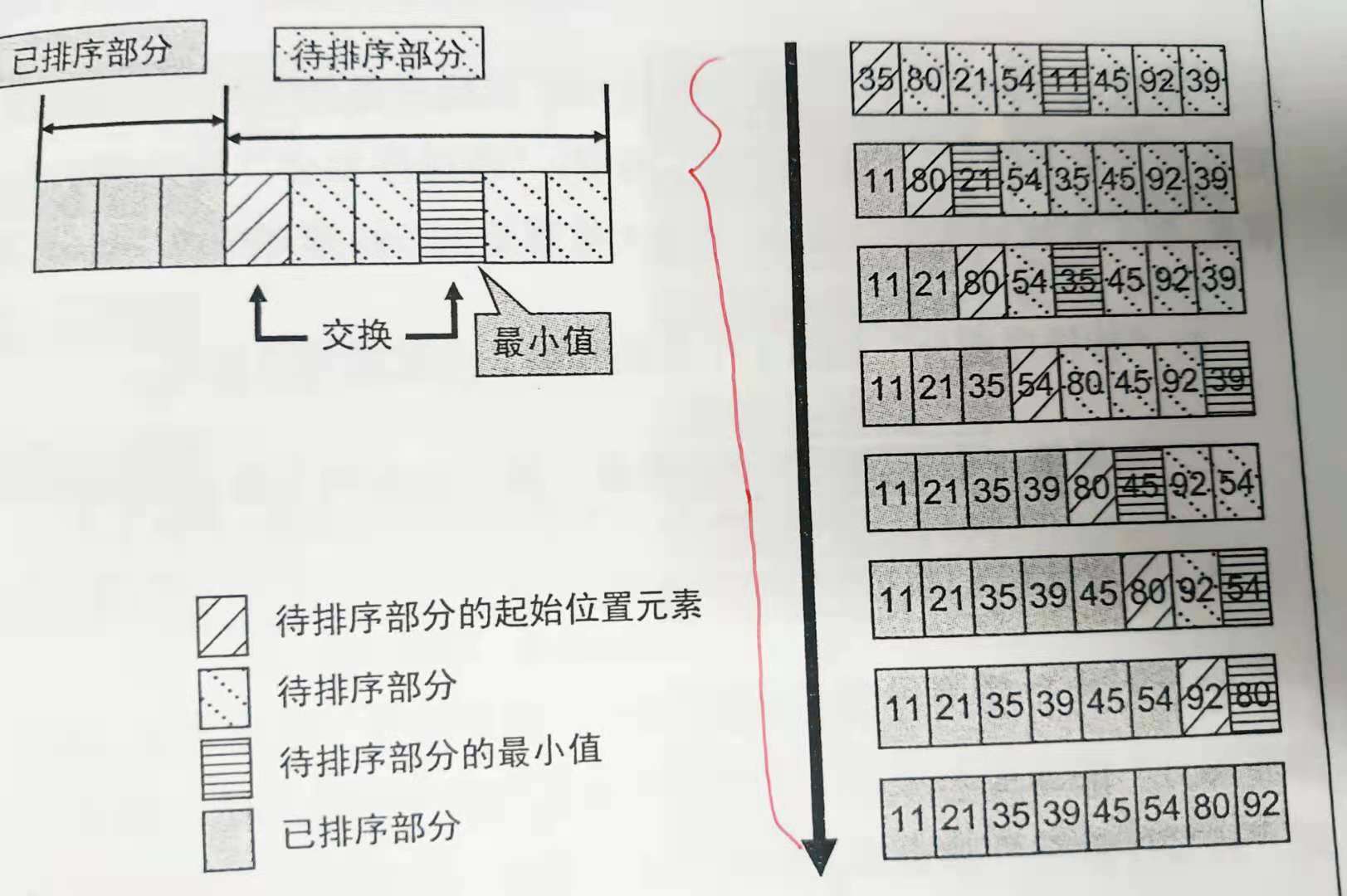
Python

#Authentic selection sorting
nums=[35,80,21,54,11,45,92,39]
n=len(nums)
for i in range(n-1):
	mid=i  #Record the first position that is not sorted at this time
	for j in range(i+1,n):
		if nums[j]<nums[mid]:
			mid=j  #If a smaller part than the first position is found in the unordered part, record its position
	nums[i],nums[mid]=nums[mid],nums[i] #The value of the first position is exchanged with the minimum value of the unordered part
print(nums)

#The selection sort is slightly modified, but the number of exchanges is more in this case,
nums=[35,80,21,54,11,45,92,39]
n=len(nums)
for i in range(n-1):
	for j in range(i+1,n):
		if nums[j]<nums[i]:
			nums[i],nums[j]=nums[j],nums[i] #If the unordered part has a smaller value than the first position, it is exchanged directly
print(nums)

out: [11, 21, 35, 39, 45, 54, 80, 92]

3. Bubble sorting

Compare adjacent elements. If the first one is bigger than the second, exchange them.

Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. After this step, the last element will be the maximum number.

Repeat the above steps for all elements except the last one.

Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.

Python

nums=[19,80,77,14,54]
n=len(nums)
for i in range(n-1):
	for j in range(1,n-i): #Take n-i, because after I cycles, the following I numbers have been arranged in order
		if nums[j-1]>nums[j]:
			nums[j-1],nums[j]=nums[j],nums[j-1]  #As long as the number on the left is greater than that on the right, swap two numbers, so that a j loop can send the maximum number to the end of the array (the unordered part)

print(nums)

out:[14, 19, 54, 77, 80]

4. Insert sort

Just focus on the first element of the part to be sorted and find out where to insert it into the sorted part

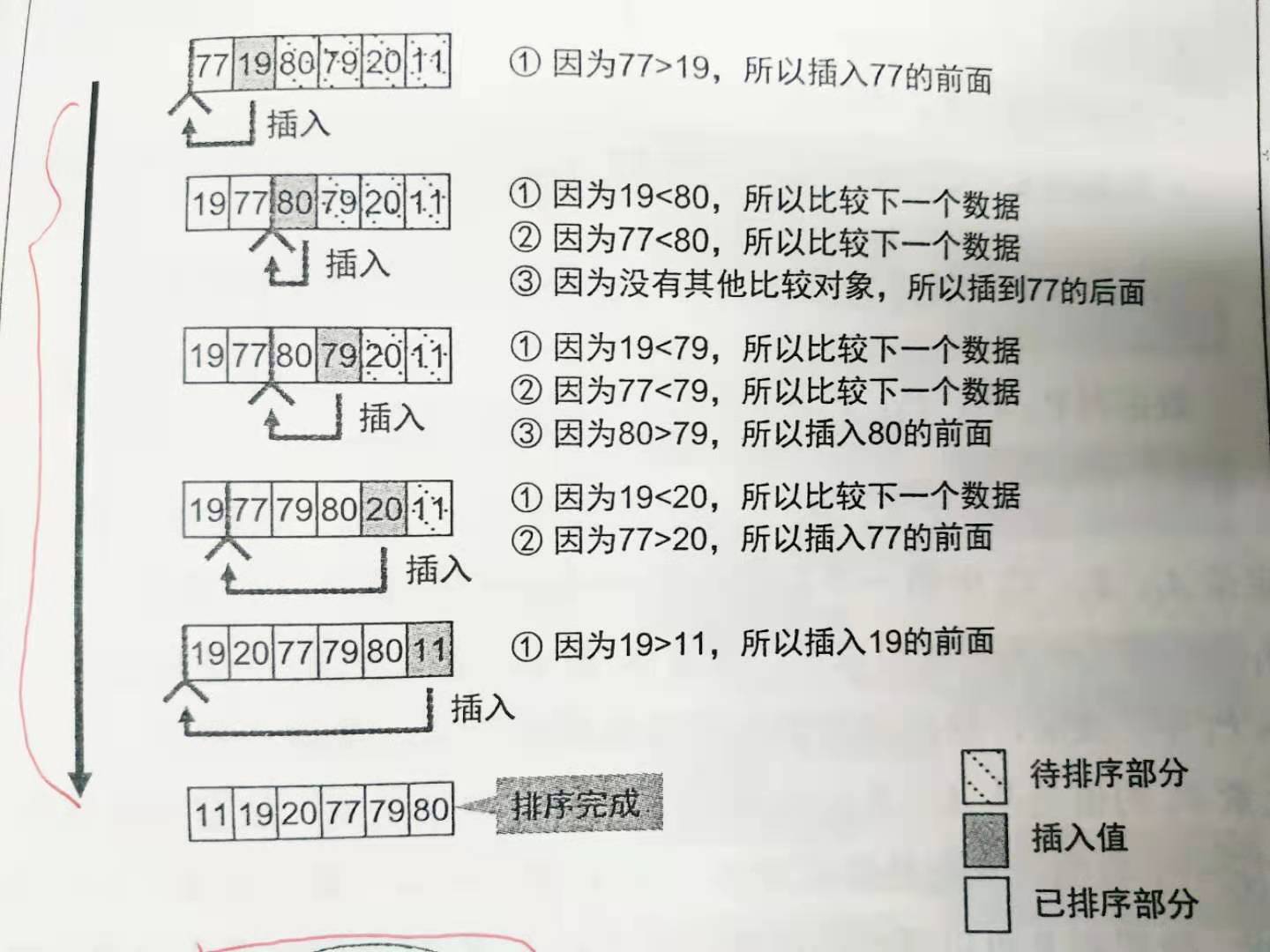
Python

nums=[77,19,80,79,20,11]
n=len(nums)

for i in range(n): #Control the number of i + 1 (serial number is i) to be inserted into the i numbers that have been ordered
	for j in range(i,0,-1): #The inner loop inserts the number I + 1 (serial number i) into the position in line with its sorting
		if nums[j-1]>nums[j]:
			nums[j-1],nums[j]=nums[j],nums[j-1]  #As long as the number on the left is greater than that on the right, swap two numbers and insert num [i] in a similar way to bubble sorting“

print(nums)

out:[11, 19, 20, 77, 79, 80]

5. Merge and sort

Merging refers to the algorithm of merging several sorted data columns into one sorted data column
Only when several data columns are sorted in ascending order, the minimum value of all data must be in the starting element of each data column
When the starting element is taken, the second element will be set as the starting element, so the minimum value of all remaining data is always in the starting element of each data column

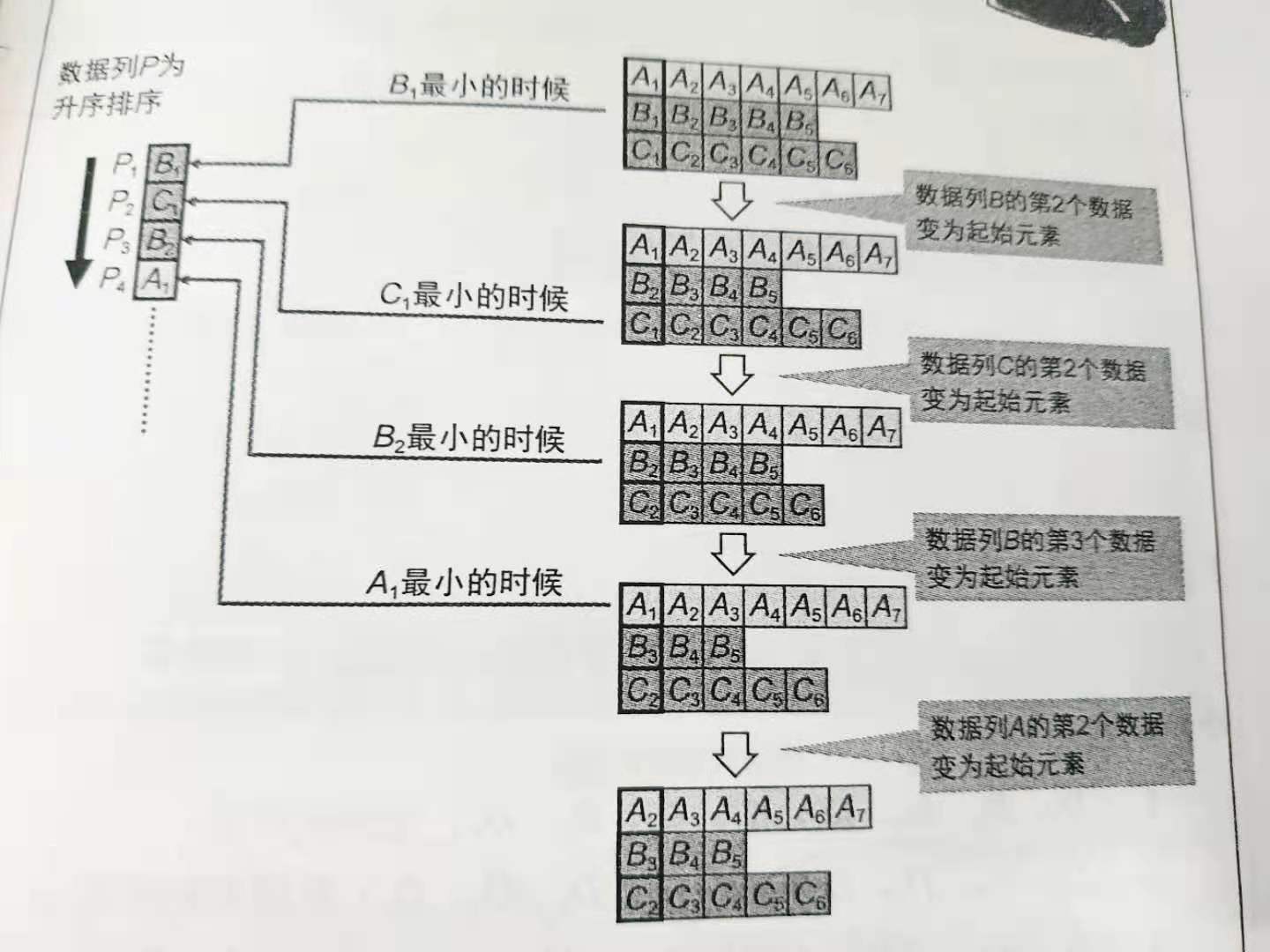
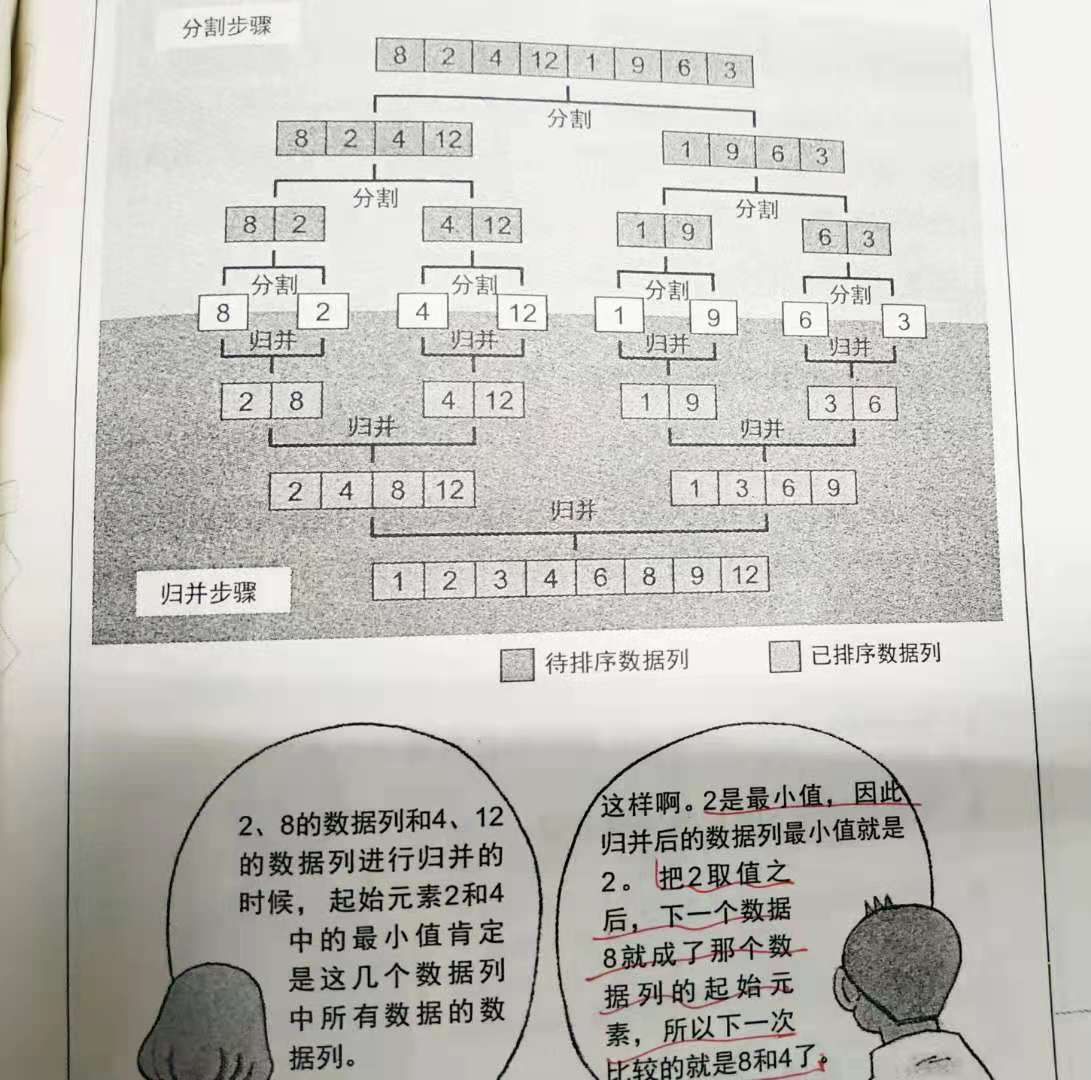
Merge sort refers to a sort algorithm that uses segmentation and merging to sort. It is mainly composed of two steps: segmentation and merging

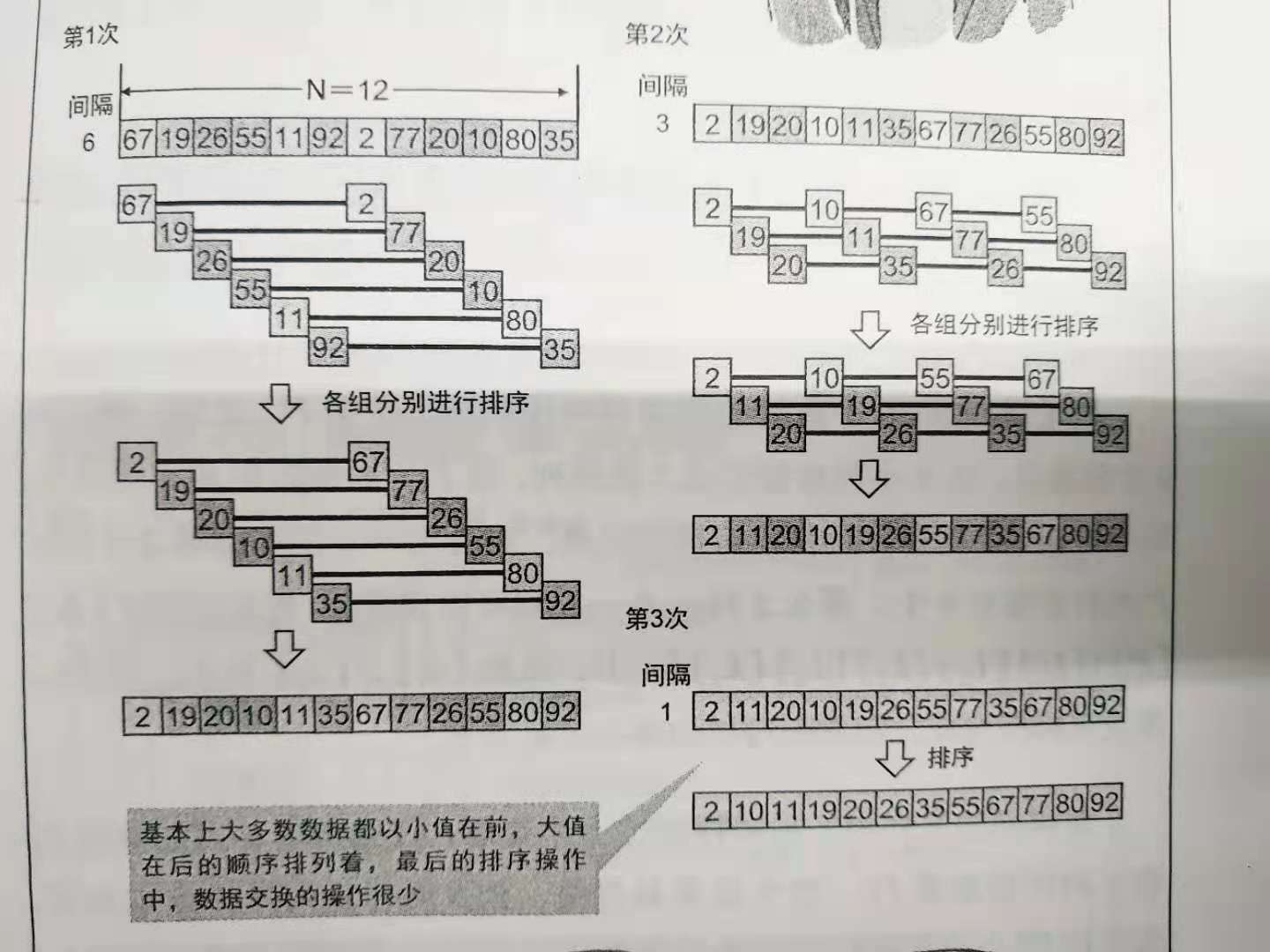
6. Hill sort

A sorting algorithm that groups data at certain intervals and sorts each group

7. Quick sort