Question 16. 3Sum Closest
Title Description (medium difficulty)
and Last question Very similar, but this is to give a target value and find three numbers to make their sum closest to the target value.
Solution - violent solution
Traverse all cases, then find the sum of the three numbers, compare with the target value, and select the one with the smallest difference. I thought the time complexity was too large. Amazingly, it turned out to be too complicated.
public int threeSumClosest(int[] nums, int target) {
int sub = Integer.MAX_VALUE; //Save the difference between and target
int sum = 0; //Save the sum of the three numbers closest to the current target
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++)
for (int k = j + 1; k < nums.length; k++) {
if (Math.abs((nums[i] + nums[j] + nums[k] - target)) < sub) {
sum = nums[i] + nums[j] + nums[k];
sub = Math.abs(sum - target);
}
}
}
return sum;
}
Time complexity: O (n) ³), Three layer circulation.
Space complexity: O (1), constant.
Solution II
suffer Last question We can sort the array first, then fix a number, and then traverse with the first and last pointers to reduce the time complexity of an O (n).
If sum is greater than target, decrease the right pointer; otherwise, increase the left pointer.
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int sub=Integer.MAX_VALUE;
int sum=0;
for(int i=0;i<nums.length;i++){
int lo=i+1,hi=nums.length-1;
while(lo<hi){
if(Math.abs((nums[lo]+nums[hi]+nums[i]-target))<sub){
sum=nums[lo]+nums[hi]+nums[i];
sub=Math.abs(sum-target);
}
if(nums[lo]+nums[hi]+nums[i]>target){
hi--;
}else{
lo++;
}
}
}
return sum;
}
Time complexity: if it is a quick sort O(logn)O(log_n)O(logn) plus o (n) ²), So it's o (n ²).
Space complexity: O (1).
total
It is very, very similar to the previous question. First sort the array, and then use the pointers at both ends. It can be said to be very elegant.
Question 17. Letter Combinations of a Phone Number
Title Description (medium difficulty)

Give a string of numbers, each number can represent several letters under the number key, and return all possible components of the letters under these numbers.
Solution I definition multiplication
I thought about using iteration and recursion. I couldn't figure it out. I came up with this algorithm.
Take the string "23" as ["a", "b", c] * ["d", "e", "f"], and multiply it with two for loops. You should understand it from the code.
public List<String> letterCombinations(String digits) {
List<String> ans = new ArrayList<String>();
for (int i = 0; i < digits.length(); i++) {
ans = mul(ans, getList(digits.charAt(i) - '0'));
}
return ans;
}
public List<String> getList(int digit) {
String digitLetter[] = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
List<String> ans = new ArrayList<String>();
for (int i = 0; i < digitLetter[digit].length(); i++) {
ans.add(digitLetter[digit].charAt(i) + "");
}
return ans;
}
//Defined as multiplying two lists
public List<String> mul(List<String> l1, List<String> l2) {
if (l1.size() != 0 && l2.size() == 0) {
return l1;
}
if (l1.size() == 0 && l2.size() != 0) {
return l2;
}
List<String> ans = new ArrayList<String>();
for (int i = 0; i < l1.size(); i++)
for (int j = 0; j < l2.size(); j++) {
ans.add(l1.get(i) + l2.get(j));
}
return ans;
}
Solution two queue iteration
reference resources here Sure enough, someone wrote it in iteration. It mainly uses queues.
public List<String> letterCombinations(String digits) {
LinkedList<String> ans = new LinkedList<String>();
if(digits.isEmpty()) return ans;
String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
ans.add("");
for(int i =0; i<digits.length();i++){
int x = Character.getNumericValue(digits.charAt(i));
while(ans.peek().length()==i){ //View team leader element
String t = ans.remove(); //The first element of the team is out of the team
for(char s : mapping[x].toCharArray())
ans.add(t+s);
}
}
return ans;
}
If it is "23", then
After the first for cycle, it becomes a, b, c;
In the first while loop of the second for loop, a goes out of the queue, adds d e f respectively, and then enters the queue, which becomes b c ad ae af
The second while loop b of the second for loop goes out of the queue, adds d e f respectively, and then enters the queue, which becomes c ad ae af bd be bf
The third while loop c of the second for loop goes out of the queue, adds d e f respectively, and then joins the team, which becomes ad ae af bd be bf cd ce cf
In this way, the element length of the queue is no longer equal to 1, and a while loop occurs.
Solution three recursion
reference resources here
private static final String[] KEYS = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
public List<String> letterCombinations(String digits) {
if(digits.equals("")) {
return new ArrayList<String>();
}
List<String> ret = new LinkedList<String>();
combination("", digits, 0, ret);
return ret;
}
private void combination(String prefix, String digits, int offset, List<String> ret) {
//offset represents which number is being added
if (offset == digits.length()) {
ret.add(prefix);
return;
}
String letters = KEYS[(digits.charAt(offset) - '0')];
for (int i = 0; i < letters.length(); i++) {
combination(prefix + letters.charAt(i), digits, offset + 1, ret);
}
}
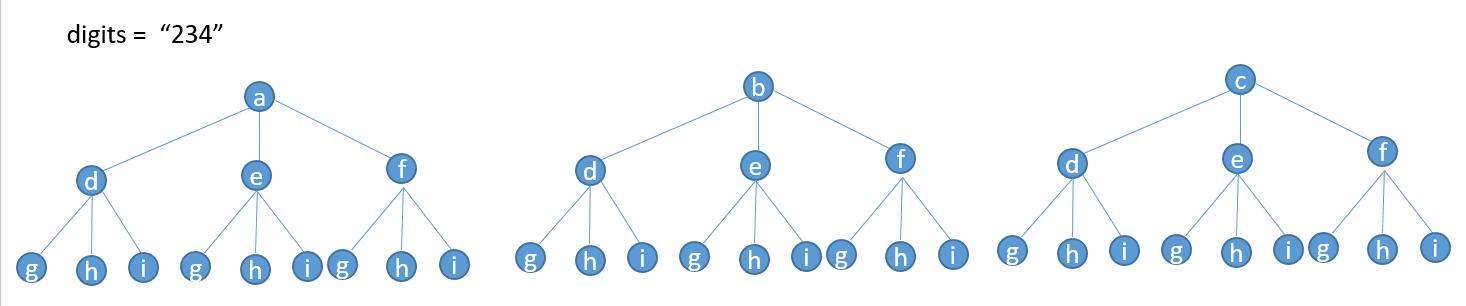
Start with a, then recurse to d, then g, add adg, then adh, and then adi... Recurse to the end from left to right, and then add it.
total
The time complexity and space complexity of this problem are not clear, so they didn't write it.
Question 18: 4Sum
Title Description (medium difficulty)
and 3Sum Similarly, it's just to find four numbers so that sum is target and there can be no duplicate sequences.
If you haven't done it before 3Sum You can have a look first. You just added a cycle on the basis of the above.
public List<List<Integer>> fourSum(int[] num, int target) {
Arrays.sort(num);
List<List<Integer>> res = new LinkedList<>();
//Additional layers of circulation
for (int j = 0; j < num.length - 3; j++) {
//Prevent duplicate
if (j == 0 || (j > 0 && num[j] != num[j - 1]))
for (int i = j + 1; i < num.length - 2; i++) {
//To prevent repetition, it is no longer i == 0, because i starts from j + 1
if (i == j + 1 || num[i] != num[i - 1]) {
int lo = i + 1, hi = num.length - 1, sum = target - num[j] - num[i];
while (lo < hi) {
if (num[lo] + num[hi] == sum) {
res.add(Arrays.asList(num[j], num[i], num[lo], num[hi]));
while (lo < hi && num[lo] == num[lo + 1])
lo++;
while (lo < hi && num[hi] == num[hi - 1])
hi--;
lo++;
hi--;
} else if (num[lo] + num[hi] < sum)
lo++;
else
hi--;
}
}
}
}
return res;
}
Time complexity: O (n) ³).
Spatial complexity: O (N). In the worst case, N refers to the number of permutations and combinations of N elements, that is, N=Cn4N=C^4_nN=Cn4, which is used to save the results.
total
It is completely written according to the idea of 3Sum, which is easy to understand.
Question 19: Remove Nth Node From End of List
Title Description (medium difficulty)
Given a linked list, delete the penultimate node.
Solution I
Deleting a node is nothing more than traversing the linked list, finding the node in front of that node, and then changing the next point. But because it is a linked list, we don't know its length. We have to traverse it first to get its length, and then subtract n from the length is the position of the node to be deleted, and then traverse to the previous position of the node.
public ListNode removeNthFromEnd(ListNode head, int n) {
int len = 0;
ListNode h = head;
while (h != null) {
h = h.next;
len++;
}
//If the length is equal to 1, deleting another node will be null
if (len == 1) {
return null;
}
int rm_node_index = len - n;
//If the head node is deleted
if (rm_node_index == 0) {
return head.next;
}
//Find the previous node of the deleted node
h = head;
for (int i = 0; i < rm_node_index - 1; i++) {
h = h.next;
}
//Change direction
h.next = h.next.next;
return head;
}
Time complexity: assuming that the length of the linked list is l, the first cycle is l times, the second cycle is L - n times, a total of 2L - n times, so the time complexity is O (L).
Space complexity: O (1).
We see that if the length is equal to 1 and the head node is deleted, we need to judge separately. In fact, we only need to add an empty node in front of the head to avoid judging separately.
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
int length = 0;
ListNode first = head;
while (first != null) {
length++;
first = first.next;
}
length -= n;
first = dummy;
while (length > 0) {
length--;
first = first.next;
}
first.next = first.next.next;
return dummy.next;
}
Solution of two traversal linked list
Above, we traverse the linked list twice. How can we traverse only once.
Yes leetcode Explanation of.
Imagine two people running a 100m race, assuming they have the same speed. At the beginning, the first person is 10m in front of the second person, so when the first person runs to the end, the second person is still 10m away from the first person, that is, 10m away from the end.
Compared with the linked list, we set two pointers, first let the first pointer traverse n steps, and then let them start traversing at the same time. In this way, when the first pointer reaches the end, the second pointer is n away from the first pointer, so the position of the second pointer is just the penultimate node.
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
//The first pointer moves n steps first
for (int i = 1; i <= n + 1; i++) {
first = first.next;
}
//The first pointer reaches the end point and stops traversal
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
Time complexity:
The first pointer goes from 0 to N, and then "the first pointer goes from n to end" and "the second pointer goes from 0 to the penultimate node".
The solution is nothing more than from 0 to the end, and then from 0 to the position of the penultimate node.
In fact, the execution times of their statements are the same. The position from 0 to the penultimate node is traversed twice, so it is also 2L - n times in total. However, this solution combines the two cycles of solution 1, making the second pointer look like passing by. The idea is very nice.
So essentially, they are the same, and the time complexity is still O (n).
Space complexity: O (1).
Solution III
Before I read the explanation, I discussed with my roommate how to traverse the linked list only once. My roommate gave me a point I couldn't refute, ha ha.
When traversing the linked list to determine the length for the first time, save each node in the array, so that you don't need to traverse again when looking for nodes. Space changes time??? Ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha ha.
public ListNode removeNthFromEnd(ListNode head, int n) {
List<ListNode> l = new ArrayList<ListNode>();
ListNode h = head;
int len = 0;
while (h != null) {
l.add(h);
h = h.next;
len++;
}
if (len == 1) {
return null;
}
int remove = len - n;
if (remove == 0) {
return head.next;
}
//Get it directly without traversal
ListNode r = l.get(remove - 1);
r.next = r.next.next;
return head;
}
Time complexity: O (L).
Space complexity: O (L).
total
Using two pointers to fix the interval first and then traverse at the same time is really wonderful! In addition, the idea of roommate is also great, ha ha ha.
Question 20: valid parents
Title Description (simple difficulty)
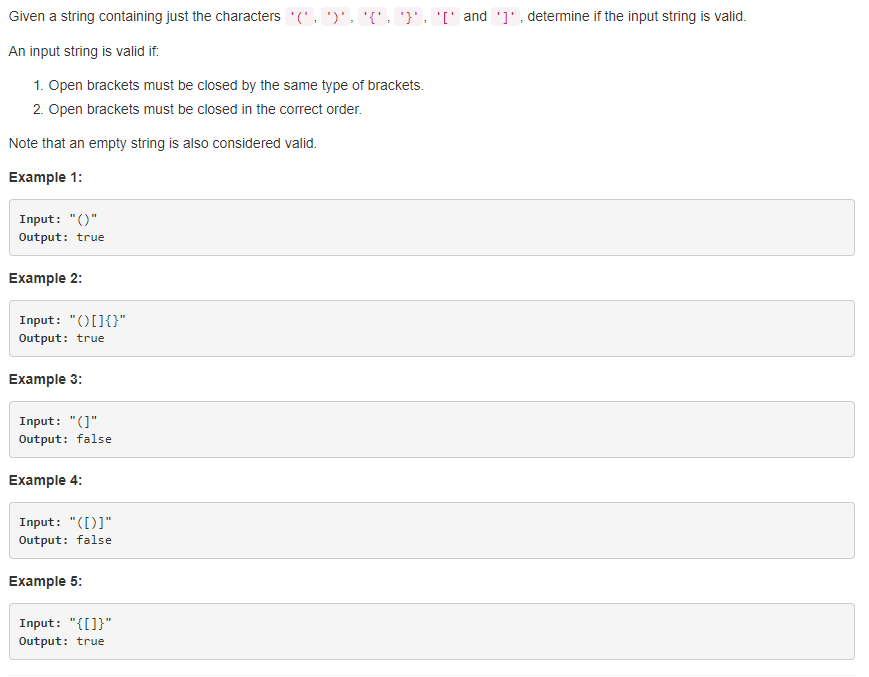
Bracket matching problem.
If there is only one kind of parenthesis, we can use a counter count to traverse the whole string. If we encounter the left parenthesis plus 1 and the right parenthesis minus 1, after traversal, if count equals 0, it means all matches. But if there are multiple parentheses, such as ([]), it will still get 0, so we need to use other methods.
Stack!
Traverse the whole string, enter the stack when encountering the left bracket, and then exit the stack when encountering the right bracket corresponding to the top of the stack. After traversal, if the stack is empty, it means all matches.
public boolean isValid(String s) {
Stack<Character> brackets = new Stack<Character>();
for(int i = 0;i < s.length();i++){
char c = s.charAt(i);
switch(c){
case '(':
case '[':
case '{':
brackets.push(c);
break;
case ')':
if(!brackets.empty()){
if(brackets.peek()== '('){
brackets.pop();
}else{
return false;
}
}else{
return false;
}
break;
case ']':
if(!brackets.empty()){
if(brackets.peek()=='['){
brackets.pop();
}else{
return false;
}
}else{
return false;
}
break;
case '}':
if(!brackets.empty()){
if(brackets.peek()=='{'){
brackets.pop();
}else{
return false;
}
}else{
return false;
}
}
}
return brackets.empty();
}
Time complexity: O (n).
Space complexity: O (n).
total
If you have learned data structures, you must have written calculators, and you must have encountered the problem of bracket matching.
Today, we learned the algorithm analysis of LeetCode problem together. Thank you for reading. I think it's good. Remember to collect it!